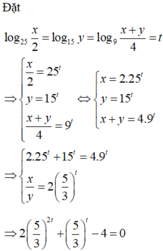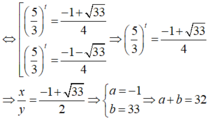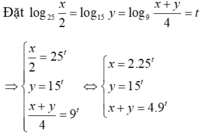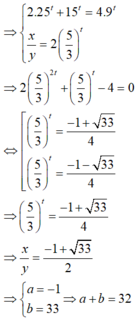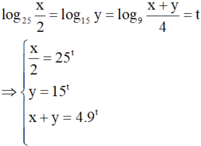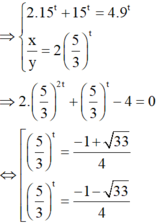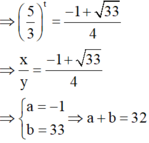cho a,b là các số nguyên dương thỏa mãn (a;65)=(b;65)=1 chứng minh a^12-b^12 chia hết cho 65
DH
Những câu hỏi liên quan
cho a b c là các số nguyên dương thỏa mãn c + 1/b = a + b/a chứng minh ab là lập phương của 1 số nguyên dương
Gọi \(d=gcd\left(a;b\right)\) khi đó \(a=dm;b=dn\) với \(\left(m;n\right)=1\)
Ta có:
\(c+\frac{1}{b}=a+\frac{b}{a}\Leftrightarrow c=\frac{b}{a}+a-\frac{1}{b}=\frac{dn}{dm}+dm-\frac{1}{dn}\)
\(=\frac{n}{m}+dm-\frac{1}{dn}=\frac{dn^2+d^2m^2n-m}{dmn}\)
Khi đó \(dn^2+d^2m^2n-m⋮dmn\Rightarrow m⋮n\) mà \(\left(m;n\right)=1\Rightarrow n=1\Rightarrow m=d\)
Khi đó \(ab=dm\cdot dn=d^3\) là lập phương số nguyên dương
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
-
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = - a + b 2 với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 32
Đáp án D
Đặt log 25 x 2 = log 15 y = log 9 x + y 4 = t ⇒ x 2 = 25 t y = 15 t x + y = 4 . 9 t
⇒ 2 . 15 t + 15 t = 4 . 9 t x y = 2 5 3 t ⇒ 2 . 5 3 2 t + 5 3 t - 4 = 0 ⇔ [ 5 3 t = - 1 + 33 4 5 3 t = - 1 - 33 4
⇒ 5 3 t = - 1 + 33 4 ⇒ x y = - 1 + 33 4 ⇒ a = - 1 b = 33 ⇒ a + b = 32 .
Đúng 0
Bình luận (0)
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
−
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = − a + b 2 , với a, b là các số nguyên dương. Tính a+b
A. 14
B. 3
C. 21
D. 32
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
19
x
+
y
4
và
x
y
-
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 19 x + y 4 và x y = - a + b 2 với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 34
Cho a,b là các số nguyên dương thỏa mãn p=a^2+b^2 là số nguyên tố và p-5 chia hết cho 8 . Giả sử x,y là các số nguyên thỏa mãn ax^2-by^2 chia hết cho p. Chứng minh rằng cả 2 số x,y chia hết cho p
Cho a,b là các số nguyên dương thỏa mãn p=a^2+b^2 là số nguyên tố và p-5 chia hết cho 8 . Giả sử x,y là các số nguyên thỏa mãn ax^2-by^2 chia hết cho p. Chứng minh rằng cả 2 số x,y chia hết cho p
p=a^2+b^2 (1)
p là số nguyên tố, p-5 chia hết 8 => p lẻ >=13 và a,b có 1 chẵn 1 lẻ
A=a.x^2-b.y^2 chia hết cho p, nên có thể viết A = p(c.x^2 -d.y^2) với c,d phải nguyên
và c.p = a và d.p = b
thay (1) vào ta thấy c=a/(a^2+b^2) cần nguyên là vô lý vậy A muốn chia hết cho p <=> x và y cùng là bội số của p
Đúng 0
Bình luận (0)
Đặt \(p=8k+5\left(đk:K\in N\right)\)
Vì: \(\left(ax^2\right)^{4k+2}-\left(by^2\right)^{4k+2}⋮\left(ax^2-by^2\right)\)
\(\Rightarrow a^{4k+2}.x^{8k+4}-b^{4k+2}.y^{8k+4}⋮p\)
Mà \(a^{4k+2}.x^{8k+4}-b^{4k+2}.y^{8k+4}\)\(=\left(a^{4k+2}+b^{4k+2}\right).x^{8k+4}-b^{4k+2}\)\(\left(x^{8k+4}+y^{8k+4}\right)\)
Ta lại có: \(a^{4k+2}+b^{4k+2}=\left(a^2\right)^{2k+1}+\left(b^2\right)^{2k+1}⋮p\) ; p<d nên \(x^{8k+4}+y^{8k+4}⋮p\)
Làm tiếp đi
Đúng 0
Bình luận (0)
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
-
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = - a + b 2 , với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 32
a) Cho a, b, c là ba số nguyên dương nguyên tố cùng nhau thỏa mãn: \(\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\) hỏi a + b có là số chính phương không? vì sao?
b) Cho x, y, z là các số dương thỏa mãn: z ≥ 60, x + y + z = 100. Tìm GTLN của A = xyz
Ta có:
\(\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\Leftrightarrow\left(a+b\right)c=ab\Leftrightarrow ab-bc-ab=0\)
Hay \(ab-bc-ab+c^2=c^2\Leftrightarrow\left(b-c\right)\left(a-c\right)=c^2\)
Nếu \(\left(b-c;a-c\right)=d\ne1\Rightarrow c^2=d^2\left(loai\right)\)
Vậy \(\left(b-c;a-c\right)=1\Rightarrow c-b;c-a\) là 2 số chính phương
Đặt \(b-c=n^2;a-c=m^2\)
\(\Rightarrow a+b=b-c+a-c+2c=m^2+n^2+2mn=\left(m+n\right)^2\) là số chính phương
cho mình hỏi tại sao ở TH1: c^2=d^2 lại loại vậy ạ
Đúng 0
Bình luận (0)
Cho a, b, c là các số nguyên dương thỏa mãn:
a + b + c > 0; ab + bc + ca; abc > 0
Chứng minh rằng cả 3 số đều là các số nguyên dương.
Các số nguyên dương a,b,c thỏa mãn: c+ 1/b = a+ b/a Chứng minh ab là lập phương 1 số nguyên dương
Mình đã làm 1 cách trong TKHĐ giờ làm cách 2 nhá
\(c+\frac{1}{b}=a+\frac{b}{a}\)
\(\Leftrightarrow c-a=\frac{b}{a}-\frac{1}{b}=\frac{b^2-a}{ab}\)
Khi đó \(b^2-a⋮ab\Leftrightarrow b^2-a=kab\) với k là số nguyên dương
Khi đó \(b^2=a\left(kb+1\right)\)
Mà \(\left(b;kb+1\right)=1\Rightarrow kb+1=1\Rightarrow kb=0\Rightarrow k=0\)
\(\Rightarrow a=b^2\Rightarrow ab=b^3\left(đpcm\right)\)