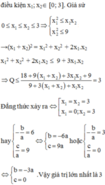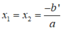Câu 1 :Giả sử phương trình bậc hai \(ax^2+bx+c=0\) có hai nghiệm thuộc [0;3]. Tìm GTLN và GTNN của biểu thức:
Q=\(\frac{18a^2-9ab+b^2}{9a^2-3ab+ac}\)
Câu 2 Giả sử phương trình bậc hai \(ax^2+bx+c=0\) có hai nghiệm > 1 Chứng minh rằng
\(\frac{^{x^2-a-2b}}{b-a+1}\text{≥}\frac{2\sqrt{b}}{1+\sqrt{b}}\)
GIÚP MÌNH VỚI