Gọi (S) là mặt cầu đi qua 4 điểm A(2;0;0),B(1;3;0),C(-1;0;3),D(1;2;3) . Tính bán kính R của (S).
A. R = 2 2
B. R = 6
C. R = 3
D. R = 6
Gọi (S) là mặt cầu đi qua 4 điểm A(2;0;0),B(1;3;0),C(-1;0;3),D(1;2;3) . Tính bán kính R của (S)
![]()
![]()
![]()
![]()
Chọn B
Phương pháp:
- Gọi I (a;b;c) là tâm mặt cầu.
- Lập hệ phương trình ẩn a,b,c
dựa vào điều kiện IA = IB = IC = ID .
Cách giải:
Gọi I (a;b;c) là tâm mặt cầu đi qua bốn điểm A(2;0;0) ,B(1;3;0) ,C(-1;0;3) ,D(1;2;3) .
<=>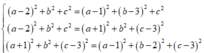
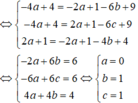
Suy ra I(0;1;1) và ![]()
Gọi (S) là tập hợp đi qua 4 điểm A(2;0;0), B(1;3;0), C(-1;0;3), D(1;2;3). Tính bán kính R của mặt cầu (S)
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho bốn điểm A(1;2;-4), B(1;-3;1), C(2;2;3), D(1;0;4). Gọi (S) là mặt cầu đi qua bốn điểmA,B,C,D. Tọa độ tâm I và bán kính R mặt cầu (S) là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho điểm A ( 0 ; 1 ; 2 ) , mặt phẳng α : x - y + z - 4 = 0 và mặt cầu S : ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 16 . Gọi (P) là mặt phẳng đi qua A, vuông góc với α và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
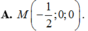
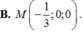
![]()
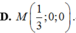
Gọi S là tập hợp đi qua 4 điểm A 2 ; 0 ; 0 , B 1 ; 3 ; 0 , C - 1 ; 0 ; 3 , D 1 ; 2 ; 3 . Tính bán kính R của mặt cầu S
A. R = 2 2
B. R = 6
C. R = 6
D. R = 3
Trong không gian Oxyz, cho điểm E(2;1;3), mặt phẳng (P) đi qua ba điểm A ( 3 2 ; 0 ; 0 ) , B ( 0 ; 3 2 ; 0 ) , C ( 0 ; 0 ; - 3 ) , và mặt cầu (S): ( x - 3 ) 2 + ( y - 2 ) 2 + ( z - 5 ) 2 = 36 . Gọi ∆ là đường thẳng đi qua điểm E, nằm trong (P) và cắt (S) tại hai điểm có khoảng cách nhỏ nhất. Phương trình ∆ là
A. x = 2 + 9 t y = 1 + 9 t z = 3 + 8 t
B. x = 2 - 5 t y = 1 + 3 t z = 3
C. x = 2 + t y = 1 - t z = 3
D. x = 2 + 4 t y = 1 + 3 t z = 3 - 3 t
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x-y+z-4=0 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)²=16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
A . M - 1 2 ; 0 ; 0
B . M - 1 3 ; 0 ; 0
C . M 1 ; 0 ; 0
D . M 1 3 ; 0 ; 0
Chọn A
Gọi ![]() là một vec tơ pháp tuyến của mặt phẳng (P).
là một vec tơ pháp tuyến của mặt phẳng (P).
Theo đề bài ta có mặt phẳng (P) vuông góc với mặt phẳng (α): x-y+z-4=0 nên ta có phương trình a-b+c=0 ó b=a+c ![]()
Phương trình mặt phẳng (P) đi qua A(0;1;2) và có véc tơ pháp tuyến là ax+ (a+c) (y-1)+c (z-2) =0
Khoảng cách từ tâm I (3;1;2) đến mặt phẳng (P) là 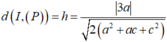
Gọi r là bán kính của đường tròn giao tuyến giữa mặt cầu (S) và mặt phẳng (P) ta có r²=16-h² ; r nhỏ nhất khi h lớn nhất.
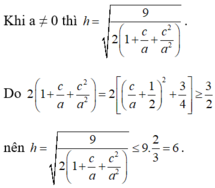
Dấu “=” xảy ra khi a = -2c. => một véc tơ pháp tuyến là ![]() => phương trình mặt phẳng (P) là 2x+y-z+1=0.
=> phương trình mặt phẳng (P) là 2x+y-z+1=0.
Vậy tọa độ giao điểm M của (P) và trục x'Ox là: 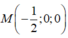
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 2 = y 1 = z - 2 và hai điểm A(2;1;0), B(-2;3;2). Gọi (S) là mặt cầu đi qua hai điểm A, B và có tâm thuộc đường thẳng d. Diện tích của mặt cầu (S) bằng
A. 68 π
B. 25 π
C. 74 π
D. 26 π
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + x + 2 2 = 16 và điểm A(m;m;2) nằm ngoài mặt cầu. Từ A kẻ các tiếp tuyến đến mặt cầu (S), gọi P m là mặt phẳng chứa các tiếp điểm, biết P m luôn đi qua một đường thẳng d cố định, phương trình đường thẳng d là:
A. 
B. 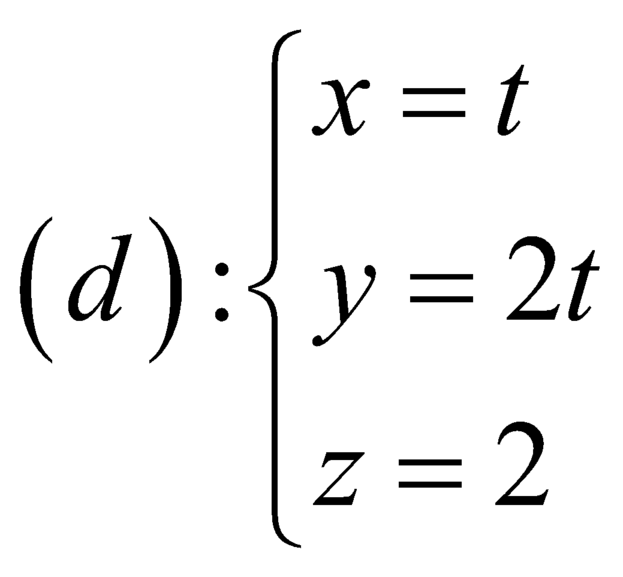
C. 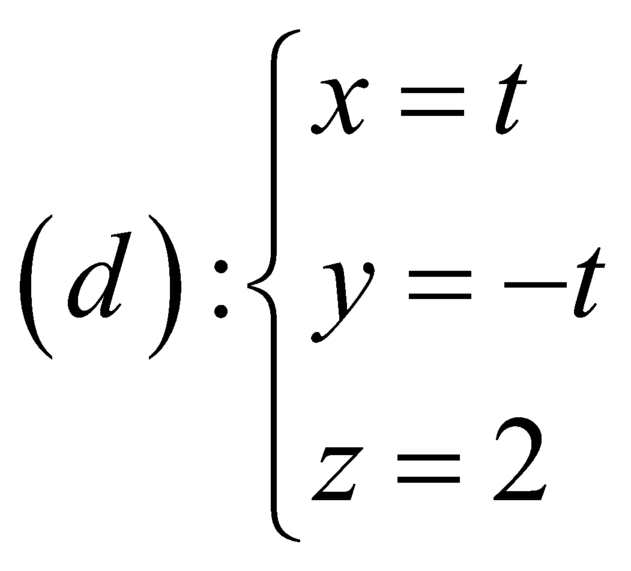
D. 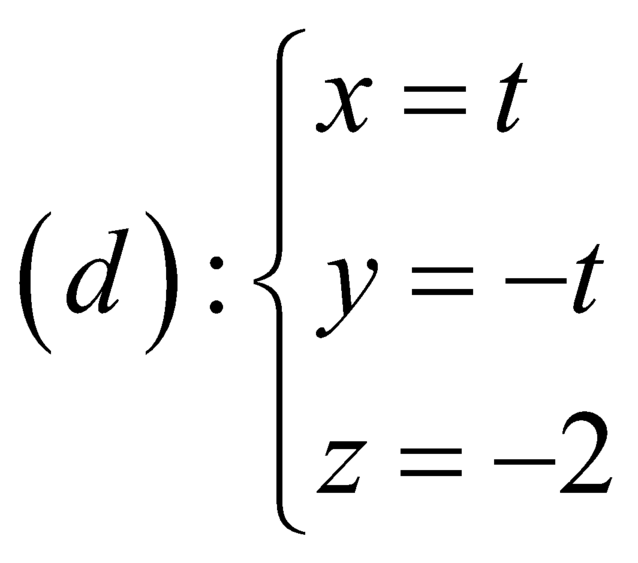 .
.