Xét x,y là các số thực thuộc đoạn [1;2]. Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức S = x y + y x Tính M + m
A.5/2
B.4
C.9/2
D. 3
PB
Những câu hỏi liên quan
Xét x,y là các số thực thuộc đoạn [1;2]. Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
S
x
y
+
y
x
. Tính M + m A.
5
2
B. 4 C.
9
2
D. 3
Đọc tiếp
Xét x,y là các số thực thuộc đoạn [1;2]. Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức S = x y + y x . Tính M + m
A. 5 2
B. 4
C. 9 2
D. 3
Xét hàm số
f
(
t
)
9
t
9
t
+
m
2
với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) 1 với mọi số thực x, y thỏa mãn
e
x
+
y...
Đọc tiếp
Xét hàm số f ( t ) = 9 t 9 t + m 2 với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) =1 với mọi số thực x, y thỏa mãn e x + y ≤ e ( x + y ) . Tìm số phần tử của S.
A. 0
B. 1
C. Vô số
D. 2
tập con S của tập số thực R gọi là đối xứng nếu với mọi x thuộc S , ta đều có -x thuộc S. Em có nhận xét gì về tập xác định của 1 hàm số chẵn (lẻ)?từ nhận xét đó em có kết luận gì về tính chẵn - lẻ của hàm số y bằng căn bậc 2 của x? tại sao?
Bài 1: Phương trìnhlog_{2} ^3(x-1)-27y^3+8^y+1-x có bao nhiêu (x;y) nghiệm thuộc [8^{1992}; 8^{2020}]Bài 2: Tìm tập hợp số thực m để phương trình 2^{2x-1}+m×2^x+2m-20 có 2 nghiệm thực phân biệt thuộc đoạn [1;2]Bài 3: Tìm các số nguyên m để phương trình log_{dfrac{1}{2}}^{2} (x-2)^3+4(m-5) log _{dfrac{1}{2}}dfrac{1}{x-2}+4m-4 có nghiệm thuộc [dfrac{5}{2};4]Bài 4: Cho phương trình (m-2)×log_{2} ^2 (x-4)-(2m+1)log_{dfrac{1}{2}} (x-4)+m+20. Tìm m để phương trình có 2 nghiệm phân biệt x1, x2 thỏa mãn...
Đọc tiếp
Bài 1: Phương trình\(\log_{2} ^3(x-1)-27y^3+8^y+1-x\) có bao nhiêu \((x;y)\) nghiệm thuộc \([8^{1992}; 8^{2020}]\)
Bài 2: Tìm tập hợp số thực m để phương trình \(2^{2x-1}+m×2^x+2m-2=0\) có 2 nghiệm thực phân biệt thuộc đoạn [1;2]
Bài 3: Tìm các số nguyên m để phương trình \(\log_{\dfrac{1}{2}}^{2} (x-2)^3+4(m-5) log _{\dfrac{1}{2}}\dfrac{1}{x-2}+4m-4\) có nghiệm thuộc \([\dfrac{5}{2};4]\)
Bài 4: Cho phương trình \((m-2)×log_{2} ^2 (x-4)-(2m+1)log_{\dfrac{1}{2}} (x-4)+m+2=0.\) Tìm m để phương trình có 2 nghiệm phân biệt x1, x2 thỏa mãn 4<x1, x2<6
Xét các số thực dương x , y thỏa mãn x + y ≤ 1 . Chứng minh rằng x + y + 1/x + 1/y ≥ 5
Ta có:
Đặt \(A=x+y+\dfrac{1}{x}+\dfrac{1}{y}\)
\(\Leftrightarrow A=x+y+\dfrac{4}{4x}+\dfrac{4}{4y}\)
\(\Leftrightarrow A=x+y+\dfrac{1}{4x}+\dfrac{3}{4x}+\dfrac{1}{4y}+\dfrac{3}{4y}\)
\(\Leftrightarrow A=\left(x+\dfrac{1}{4x}\right)+\left(y+\dfrac{1}{4y}\right)+\left(\dfrac{3}{4x}+\dfrac{3}{4y}\right)\)
\(\Rightarrow A\ge2\sqrt{x.\dfrac{1}{4x}}+2\sqrt{y.\dfrac{1}{4y}}+\dfrac{3}{4}.\dfrac{4}{x+y}\)
\(\ge2.\sqrt{\dfrac{1}{4}}+2\sqrt{\dfrac{1}{4}}+\dfrac{3}{4}.\dfrac{4}{1}\)
\(=2.\dfrac{1}{2}+2.\dfrac{1}{2}+3=1+1+3=5\)
Vậy ta có đpcm. Dấu"=" xảy ra\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{4x}\\y=\dfrac{1}{4y}\\x=y\\x+y=1\end{matrix}\right.\) \(\Leftrightarrow x=y=\dfrac{1}{2}\left(tm\right)\)
Đúng 3
Bình luận (0)
Số các giá trị thực của tham số m để phương trình (sin x-1)(2cos^2 x - (sinx -1)(2
cos
2
x
–(2m+1)cosx+m)0 có đúng 4 nghiệm thực thuộc đoạn
0
;
2
π
là A. 1. B. 2. C. 3. D. Vô số.
Đọc tiếp
Số các giá trị thực của tham số m để phương trình (sin x-1)(2cos^2 x - (sinx -1)(2 cos 2 x –(2m+1)cosx+m)=0 có đúng 4 nghiệm thực thuộc đoạn 0 ; 2 π là
A. 1.
B. 2.
C. 3.
D. Vô số.
Đáp án B.
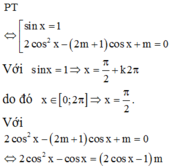
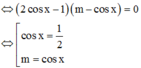
PT: cos x = 1 2 có 2 nghiệm thuộc trên đoạn 0 ; 2 π do đó để PT đã cho có 4 nghiệm thực thuộc đoạn 0 ; 2 π thì
TH1: m= cosx có 1 nghiệm thuộc đoạn 0 ; 2 π
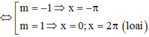
TH2: m= cosx có 2 nghiệm thuộc đoạn 0 ; 2 π trong đó có 1 nghiệm trùng
Vậy m= -1; m=0.
Đúng 0
Bình luận (0)
Xét x, y là các số thực dương thỏa mãn
log
2
x
+
4
y
x
+
y
2
x
-
4
y
+
1
. Giá trị nhỏ nhất của
P
2
x
4...
Đọc tiếp
Xét x, y là các số thực dương thỏa mãn log 2 x + 4 y x + y = 2 x - 4 y + 1 . Giá trị nhỏ nhất của P = 2 x 4 - 2 x 2 y 2 + 6 x 2 x + y 3 bằng
A. 25 9
B. 4
C. 9 4
D. 16 9
Xét các số thực dương x , y , z thỏa mãn x + y + z ≤ 1 . Chứng minh rằng x + y + z + 1/x + 1/y + 1/z ≥ 10 .
Đặt \(A=x+y+z+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\)
\(\Leftrightarrow A=x+y+z+\dfrac{9}{9x}+\dfrac{9}{9y}+\dfrac{9}{9z}\)
\(\Leftrightarrow A=x+y+z+\dfrac{1}{9x}+\dfrac{8}{9x}+\dfrac{1}{9y}+\dfrac{8}{9y}+\dfrac{1}{9z}+\dfrac{8}{9z}\)
\(\Leftrightarrow A=\left(x+\dfrac{1}{9x}\right)+\left(y+\dfrac{1}{9y}\right)+\left(z+\dfrac{1}{9z}\right)+\left(\dfrac{8}{9x}+\dfrac{8}{9y}+\dfrac{8}{9z}\right)\)
\(\Leftrightarrow A=\left(x+\dfrac{1}{9x}\right)+\left(y+\dfrac{1}{9y}\right)+\left(z+\dfrac{1}{9z}\right)+\dfrac{8}{9}.\left(\dfrac{1^2}{x}+\dfrac{1^2}{y}+\dfrac{1^2}{z}\right)\)
\(\Rightarrow A\ge2\sqrt{x.\dfrac{1}{9x}}+2\sqrt{y.\dfrac{1}{9y}}+2\sqrt{z.\dfrac{1}{9z}}+\dfrac{8}{9}.\dfrac{\left(1+1+1\right)^2}{x+y+z}\)
\(\Rightarrow A\ge2\sqrt{\dfrac{1}{9}}+2\sqrt{\dfrac{1}{9}}+2\sqrt{\dfrac{1}{9}}+\dfrac{8}{9}.\dfrac{3^2}{1}\)
\(\Rightarrow A\ge2.\dfrac{1}{3}.3+8=2+8=10\)
Vậy ta có BĐT cần chứng minh.
Dấu\("="\) xảy ra\(\Leftrightarrow x=y=z=\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
Xét x, y là các số thực thỏa mãn điều kiện
x
2
+
y
2
1
. Đặt
S
2
x
2
+
6
x
y
x
2...
Đọc tiếp
Xét x, y là các số thực thỏa mãn điều kiện x 2 + y 2 = 1 . Đặt S = 2 x 2 + 6 x y x 2 + 2 x y + 3 y 2 . Khẳng định nào sau đây là đúng?
A. Biểu thức S không có giá trị nhỏ nhất
B. min S = -6
C. Biểu thức S không có giá trị lớn nhất
D. max S = 2
