Trong không gian với hệ trục Oxyz, cho tam giác ABC với A(2;0;-3); B(-1;-2;4); C(2;-1;2). Biết điểm E(a,b,c) là điểm để biểu thức P = E A → + E B → + E C → đạt giá trị nhỏ nhất. Tính T=a+b+c
A. T=3
B. T=1
C. T=0
D. T=-1
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC với A(1;-3;4), B(-2;-5;-7) và C(6;-3;-1). Phương trình đường trung tuyến AM của tam giác ABC là:
A. d : x = 1 + t y = - 1 - 3 t z = - 8 - 4 t
B. d : x = 1 - 3 t y = - 3 - 2 t z = 4 - 11 t
C. d : x = 1 + t y = - 3 - t z = 4 - 8 t
D. d : x = 1 + 3 t y = - 3 + 4 t z = 4 - t
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC với A(1;-3;4), B(-2;-5;-7) và C(6;-3;-1). Phương trình đường trung tuyến AM của tam giác ABC là:
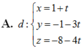
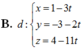
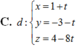
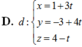
Trong không gian với hệ trục tọa độ Oxyz cho A(1;1;0), B(2;−1;1), C(3;−1;1). Tính diện tích S của tam giác ABC.
A. 5 2
B. 3
C. 3 2
D. 5
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết A ( 3 ; 1 ; 2 ) , B ( 1 ; − 4 ; 2 ) , C ( 2 ; 0 ; − 1 ) . Tìm tọa độ tâm G của tam giác ABC
A. G (2;-1;1).
B. G (6;-3;3).
C. G (2;1;1).
D. G (2;-1;3).
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(2;2;-2), B(-3;5;1), C(1;1;-2).Tìm toạ độ trọng tâm G của tam giác ABC ?
A. G(0;2;-1)
B. G(0;2;3)
C. G(0;-2;-1)
D. G(2;5;-2)
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(2;2;-2), B(-3;5;1), C(1;1;-2) Tìm toạ độ trọng tâm G của tam giác ABC ?
A. G(0;2;-1)
B. G(0;2;3)
C. G(0;-2;-1)
D. G(2;5;-2)
Đáp án A.
G 2 − 3 + 1 3 ; 2 + 5 − 1 3 ; − 2 + 1 − 2 3 = 0 ; 2 ; − 1 .
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A 2 ; 0 ; 0 ; B 0 ; 3 ; 1 ; C − 1 ; 4 ; 2 . Độ dài đường cao đỉnh A của tam giác ABC
A. 6
B. 2
C. 3 2
D. 3
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(2;0;0), B(0;3;1), C(-1;4;2). Độ dài đường cao đỉnh A của tam giác ABC
A. 6
B. 2
C. 3 2
D. 3
Đáp án B
Phương pháp
Đường thẳng d có VTCP u → và đi qua điểm M

Cách giải
Ta có
![]()
![]()

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(2;0;0), B(0;3;1), C(-1;4;2). Độ dài đường cao đỉnh A của tam giác ABC
A. 6
B. 2
C. 3 2
D. 3
Đáp án B
Phương pháp
Đường thẳng d có VTCP u → và đi qua điểm M
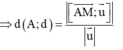
Cách giải
Ta có
![]()
![]()
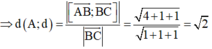
Trong không gian với hệ trục Oxyz, cho tam giác ABC có A 3 ; 3 ; 2 , B − 1 ; 2 ; 0 , C 1 ; 1 ; − 2 . Gọi G x 0 ; y 0 ; z 0 là trọng tâm của tam giác đó. Tổng x 0 + y 0 + z 0 bằng
A. 9.
B. 1 3 .
C. − 2 3 .
D. 3.