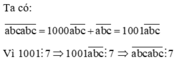Chứng minh rằng :
a) abcabc [giá trị tuyệt đối] chia hết cho 7;11 và 13
b) abcdeg [giá trị tuyệt đối] chia hết cho 23 biết :
abc [giá trị tuyệt đối] = 2 x deg [giá trị tuyệt đối]
P/s : giá trị tuyệt đối là cái gạch ngang trên đầu í
US
Những câu hỏi liên quan
Chứng minh rằng nếu a chia hết cho b thì giá trị tuyệt đối của a chia hết cho giá trị tuyệt đối của b.
MIK CẦN GẤP,AI GIẢI ĐÚNG MIK t**k CHO.
Vì |a| = +-a và |b| = +-b => |a| : |b| = (+-a) : (+-b) = +-(a:b)
Mà a chia hết cho b => a : b = k ( k thuộc Z )
=> |a| : |b| = +-k thuộc Z => |a| chia hết cho |b|
Đúng 0
Bình luận (0)
Chứng minh rằng nếu a chia hết cho b thì trị tuyệt đối của a sẽ chia hết cho trị tuyệt đối của b
Tìm x biết giá trị tuyệt đối của 3/2x+ giá trị tuyệt đối của 5/7y-1/2 nhỏ hơn hoặc bằng 0
2)chứng minh rằng 81^10-27^13-9^21 chia hết cho 225Giúp đi mình tick cho
2)81^10-27^13-9^21=3^40-3^39-3^42=3^39(3-1-3^3) =3^39.(-25)=3^37.9.(-25)=3^37.(-225) chia hết cho 225
Đúng 1
Bình luận (0)
Bài1:Tìm x biết:
a)2x-10-[3x-14-(4-5x)-2x]=2
b) (1/4x-1)+(5/6x-2)-(3/8x+1)
c)3 nhân giá trị tuyệt đối x=x+12
d)giá trị tuyệt đối x-3=giá trị tuyệt đối 2x+1
Bài 2 :
a)Chứng minh rằng tổng của 3 số nguyên liên tiếp thì chia tất cho 3
b)Chứng minh rằng tổng của 5 sồ nguyên liên tiếp thì chia tất cho 5
c)Nêu bài toán tổng quát và chứng minh rằng bài toán đó
Bài 1:
a. $2x-10-[3x-14-(4-5x)-2x]=2$
$2x-10-3x+14+(4-5x)+2x=2$
$-x-10+14+4-5x+2x=2$
$-4x+8=2$
$-4x=-6$
$x=\frac{-6}{-4}=\frac{3}{2}$
b. Đề sai. Bạn xem lại.
c.
$|x-3|=|2x+1|$
$\Rightarrow x-3=2x+1$ hoặc $x-3=-(2x+1)$
$\Rightarrow x=-4$ hoặc $x=\frac{2}{3}$
Đúng 0
Bình luận (0)
Bài 2:
a. Gọi 3 số nguyên liên tiếp là $a, a+1, a+2$
Ta có:
$a+a+1+a+2=3a+3=3(a+1)\vdots 3$ (đpcm)
b. Gọi 5 số nguyên liên tiếp là $a, a+1, a+2, a+3, a+4$
Ta có:
$a+(a+1)+(a+2)+(a+3)+(a+4)=5a+10=5(a+2)\vdots 5$ (đpcm)
c.
Tổng quát: Tổng của $n$ số nguyên liên tiếp chia hết cho $n$. với $n$ lẻ.
Thật vậy, gọi $n$ số nguyên liên tiếp là $a, a+1, a+2, ...., a+n-1$
Tổng của $n$ số nguyên liên tiếp là:
$a+(a+1)+(a+2)+....+(a+n-1)$
$=na+(1+2+3+....+n-1)$
$=na+\frac{n(n-1)}{2}$
$=n[a+\frac{n-1}{2}]$
Vì $n$ lẻ nên $\frac{n-1}{2}$ nguyên
$\Rightarrow a+\frac{n-1}{2}$ nguyên
$\Rightarrow a+(a+1)+....+(a+n-1)=n[a+\frac{n-1}{2}]\vdots n$
Đúng 0
Bình luận (0)
Cho giá trị tuyệt đối a-c < 3, giá trị tuyệt dối b-c < 2 . Chứng minh rằng giá trị tuyệt đối a-b < 5
Chứng minh rằng a b c a b c ¯ chia hết cho 7
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Phân tích số. Bước 2. Áp dụng tính chất chia hết của một tích. |
Ta có: a b c a b c ¯ = 1000 a b c ¯ + a b c ¯ = 1001 a b c ¯ Vì 1001 ⋮ 7 ⇒ 1001 a b c ¯ ⋮ 7 ⇒ a b c a b c ¯ ⋮ 7 |
Đúng 0
Bình luận (0)
Chứng minh rằng a b c a b c ¯ chia hết cho 7
7)Chứng minh rằng :
a) abcabc chia hết cho 7,11,13
b) abcdeg chia hết cho 23 và 29 , biết rằng abc=2.deg
8)Chứng minh rằng nếu ab+cd+eg chia hết cho 11 thì abcdeg chia hết cho 11
7)a) abcabc : abc = 1001
abcabc = 1001 x abc . Mà 1001 chia hết cho 7; 11; 13 nên 1001 x abc chia hết cho 7; 11; 13 . Vậy abcabc chia hết cho 7; 11; 13 ( đpcm)
b .Vì abc = 2 . deg nên abcdeg : deg = 2001
abcdeg = 2001 x deg. Do 2001 chia hết cho 23 và 29 nên 2001 x deg chia hết cho 23 và 29 . Vậy abcdeg chia hết cho 23 và 29 ( đpcm)
Đúng 0
Bình luận (0)
Ta có :
abcabc = 1000abc + abc
= 1001 . abc
= 7 . 11 . 13 . abc chia hết cho 7 ; 11 ; 13
Đúng 0
Bình luận (0)
Chứng minh rằng abcabc + ababab chia hết cho 7
phân tích ra rồi cộng lại sẽ đc số chia hết cho 7
Đúng 0
Bình luận (0)
abcabc = 100000a+10000b+1000c+100a+10b+c
ababab= 100000a+10000b+1000a+100b+10a+b
=> (abcabc+ababab) = 100000a+10000b+1000c+100a+10b+c+ 100000a+10000b+1000a+100b+10a+b
= 201110a+22111b+1001c
= 91.(2210a+221b+11c)
= 7.13.(2210a+221b+11c)
=> (abcabc+ababab) \(⋮\)7
Đúng 0
Bình luận (0)
abcabc = 100000a+10000b+1000c+100a+10b+c
ababab= 100000a+10000b+1000a+100b+10a+b
=> (abcabc+ababab) = 100000a+10000b+1000c+100a+10b+c+ 100000a+10000b+1000a+100b+10a+b
=> (abcabc+ababab)= 201110a+22111b+1001c
=> (abcabc+ababab) = 91.(2210a+221b+11c) = 7.13.(2210a+221b+11c)
=> (abcabc+ababab) \(⋮\)7
Đúng 0
Bình luận (0)