Trong mặt phẳng tọa độ Oxyz, cho mặt phẳng
( α ): x -2y + 2z - 11 = 0 và điểm M (0;1;1). Tính
khoảng cách h từ điểm M đến mặt phẳng ( α ).
A. h = 1
B. h = 2
C. h = 3
D. h = 4
Trong mặt phẳng tọa độ Oxyz, cho mặt phẳng α : x − 2 y + 2 z − 11 = 0 và điểm M(0;0;1). Tính khoảng cách h từ điểm M đến mặt phẳng α .
A. h = 1.
B. h = 2.
C. h = 3.
D. h = 4.
Trong không gian với hệ tọa độ Oxyz cho điểm M 1 ; 0 ; 6 và mặt phẳng α có phương trình là x + 2 y + 2 z − 1 = 0 . Viết phương trình mặt phẳng β đi qua M và song song với α
A. β : x + 2 y + 2 z + 13 = 0.
B. β : x + 2 y + 2 z − 15 = 0.
C. β : x + 2 y + 2 z − 13 = 0.
D. β : x + 2 y + 2 z + 15 = 0.
Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;6;7) và mặt phẳng ( P ) : x + 2 y + 2 z - 11 = 0 . Gọi (S) là mặt cầu tâm I và tiếp xúc với mặt phẳng (P). Tọa độ tiếp điểm M của mặt phẳng (P) và mặt cầu (S) là
A. (2;3;1)
B. (3;2;1)
C. (1;2;3)
D. (3;1;2)
Chọn C
Tiếp điểm là hình chiếu vuông góc của I lên mặt phẳng (P)
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A 0 ; 1 ; 1 , B 1 ; 2 ; - 1 , C 1 ; 2 ; 2 và mặt phẳng α : x + 2 y + 2 z - 1 = 0 Xét điểm M thay đổi thuộc mặt phẳng α , giá trị nhỏ nhất của biểu thức M A 2 + M B 2 + 2 M B → M C → bằng
A. 25 4
B. 17 4
C. 13 2
D. 11 2
Chọn đáp án D
Chú ý: Để giải quyết bài toán cực trị hình học không gian này ta thường dùng kiến thức liên quan đến tâm tỉ cự.


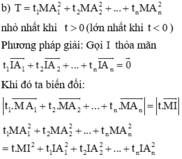
Do đó điểm cần tìm chính là hình chiếu của điểm I lên đường thẳng d(hoặc mặt phẳng (P)).
STUDY TIP |
Cách tìm tâm tỉ cự trong các bài toán mở rộng: Ta có:
|
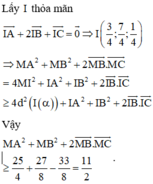
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3) và mặt phẳng α : x - 2 y + z - 12 = 0 . Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng α
A. H(5;-6;7)
B. H(2;0;4)
C. H(3;-2;5)
D. H(-1;6;1)
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng α : x + y - z + 1 = 0 v à β : - 2 x + m y + 2 z - 2 = 0 . Tìm m để mặt phẳng (α) song song với mặt phẳng (β).
A. m = 2
B. m = 5
C. Không tồn tại
D. m = -2
Trong hệ tọa độ Oxyz , cho hai mặt phẳng (P)=x+2y+2z+11=0 và (Q): x+2y+2z+2=0. Khoảng cách giữa (P) và (Q) là
A. 9
B. 3
C. 1
D. 1
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α):2x-2y-z+3=0 và điểm M(1;-2;13). Tính khoảng cách từ điểm M đến mặt phẳng ( α ) .
A. d(M, ( α ) )= 4/3
B. d(M, ( α ) )= 2/3
C. d(M, ( α ) )= 5/3
D. d(M, ( α ) )= 4
Trong không gian với trục tọa độ Oxyz, cho đường thẳng
∆ : x - 1 2 = y - 1 = z + 2 3 và mặt phẳng ( α ): x-2y+2z-3=0.
Đường thẳng đi qua O, vuông góc với ∆ và song song với
mặt phẳng ( α ) có phương trình
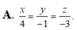
![]()
![]()
![]()