Tìm hình chiếu vuông góc của điểm M ( 3;1) trên đường thẳng \(\Delta:\left\{{}\begin{matrix}x=-2-2t\\y=1+2t\end{matrix}\right.\)
HC
Những câu hỏi liên quan
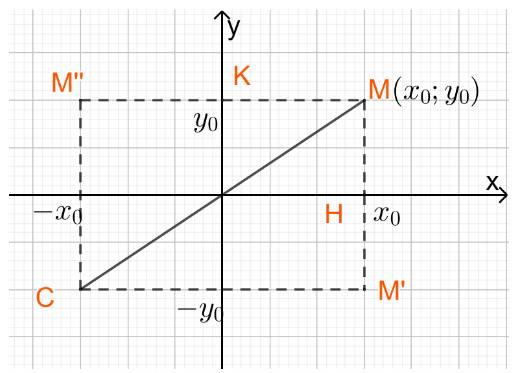
Cho điểm \(M\left( {{x_0};{y_0}} \right)\). Tìm tọa độ
a) Điểm H là hình chiếu vuông góc của M trên trục Ox
b) Điểm M’ đối xứng với M qua trục Ox
c) Điểm K là hình chiếu vuông góc của M trên trục Oy
d) Điểm M’’ đối xứng với M qua trục Oy
e) Điểm C đối xứng với M qua gốc tọa độ
a) H là hình chiếu vuông góc của M trên trục Ox nên tọa độ điểm H là \(H\left( {{x_0};0} \right)\)
b) M’ đối xứng với M qua trục Ox nên H là trung điểm của MM’
Suy ra \({x_{M'}} = 2{x_H} - {x_M} = 2{x_0} - {x_0} = {x_0};{y_{M'}} = 2{y_H} - {y_M} = 2.0 - {y_0} = - {y_0}\)
Vậy tọa độ điểm M’ là \(\left( {{x_0}; - {y_0}} \right)\)
c) K là hình chiếu vuông góc của M trên trục Oy nên tọa độ điểm K là \(K\left( {0;{y_0}} \right)\)
d) M’’ đối xứng với M qua trục Oy nên K là trung điểm của MM’’
Suy ra \({x_{M''}} = 2{x_K} - {x_M} = 2.0 - {x_0} = - {x_0};{y_{M''}} = 2{y_K} - {y_M} = 2{y_0} - {y_0} = {y_0}\)
Vậy tọa độ điểm M'' là \(\left( { - {x_0};{y_0}} \right)\)
e) C đối xứng với M qua gốc tọa độ nên O là trung điểm của MC
Suy ra \({x_C} = 2{x_O} - {x_M} = 2.0 - {x_0} = - {x_0};{y_C} = 2{y_O} - {y_M} = 2.0 - {y_0} = - {y_0}\)
Vậy tọa độ điểm C là \(\left( { - {x_0}; - {y_0}} \right)\)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho điểm M - 2 ; 5 ; 0 .Tìm hình chiếu vuông góc của điểm M trên trục Oy.
A. M'(-2;0;0)
B. M'(2;5;0)
C. M'(0;-5;0)
D. M'(0;5;0)
Trong không gian Oxyz cho điểm M(-3;2;5) Tìm tọa độ điểm M’ là hình chiếu vuông góc của điểm M trên trục Ox A. M’(3;-2;-5) B. M’(-3;0;0) C. M’(0;2;0) D. M’(0;0;5)
Đọc tiếp
Trong không gian Oxyz cho điểm M(-3;2;5) Tìm tọa độ điểm M’ là hình chiếu vuông góc của điểm M trên trục Ox
A. M’(3;-2;-5)
B. M’(-3;0;0)
C. M’(0;2;0)
D. M’(0;0;5)
Vì M’ là hình chiếu vuông góc của điểm M trên trục Ox nên M’(3 ;-2 ;-5)
Đáp án B
Đúng 0
Bình luận (0)
Cho điểm M ( 1 ; 2 ; - 3 ) , hình chiếu vuông góc của điểm M trên mặt phẳng (Oxy) là:
A. M'(1;2;0).
B. M'(1;0;-3).
C. M'(0;2;-3).
D. M'(1;2;3).
Chọn A.
Với M(a, b, c) thì hình chiếu vuông góc của M lên mặt phẳng (Oxy) là M_1(a;b;0)
Do đó,hình chiếu của điểm M(1;2;-3) lên mặt phẳng (Oxy) là điểm M’(1;2;0).
Đúng 0
Bình luận (0)
Tìm tọa độ hình chiếu vuông góc H của điểm M(1; 2; -4) trên trục Oz
A. H(0;2;0)
B. H(1;0;0)
C. H(0;0;–4)
D. H(1;2;–4)
Cho điểm M ( 1 ; 2 ; - 3 ) , hình chiếu vuông góc của điểm M trên mặt phẳng (Oxy) là:
A. M'(1;2;0)
B. M'(1;0;-3)
C. M'(0;2;-3)
D. M'(1;2;3)
Chọn A.
Với M (a,b,c) thì hình chiếu vuông góc của M lên mặt phẳng (Oxy) là M1(a;b;0)
Do đó, hình chiếu của điểm M(1;2;-3) lên mặt phẳng (Oxy) là điểm M’(1;2;0).
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho điểm M 2 ; - 3 ; 5 . Tìm tọa độ hình chiếu vuông góc của M trên trục Oy.
A. (2;0;5)
B. (0;-3;0)
C. (0;0;5)
D. (2;0;0)
Trong không gian Oxyz, cho điểm M - 1 ; 2 ; 5 . Tìm tọa độ hình chiếu vuông góc của M trên mặt phẳng tọa độ (Oyz).
A. A(-1;0;0)
B. B(0;2;5)
C. C(-1;0;5)
D. D(-1;2;0)
Trong không gian với hệ tọa độ Oxyz, cho điểm
M
2
;
−
1
;
1
. Tìm tọa độ điểm M¢ là hình chiếu vuông góc của M trên mặt phẳng (Oxy) A.
M
2
;
−
1
;
0
B.
M
0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M 2 ; − 1 ; 1 . Tìm tọa độ điểm M¢ là hình chiếu vuông góc của M trên mặt phẳng (Oxy)
A. M ' 2 ; − 1 ; 0
B. M ' 0 ; 0 ; 1
C. M ' − 2 ; 1 ; 0
D. M ' 2 ; 1 ; − 1
Đáp án A.
Tọa độ điểm M 2 ; − 1 ; 1 trên mặt phẳng (Oxy) là M ' 2 ; − 1 ; 0 .
Đúng 0
Bình luận (0)
Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M(1; -1; 2) trên mặt phẳng (α): 2x – y + 2z + 11 = 0.
Vecto pháp tuyến của mp α là n → =(2;-1;2), H là hình chiếu vuông góc của M trên mp α nên M H ⊥ m p α , đường thẳng MK có vecto pháp tuyến n → = ( 2 ; - 1 ; 2 )
Ta có pt tham số của đường thẳng MH là : x = 1 + 2 t y = - 1 - t z = 2 + 2 t
Thay x,y,z từ pt tham số của đường thẳng MH và pt mp α , ta có:
2(1+2t)-(-1-t)+2(2+2t)+11=0 <=> t=-2
Vậy H(-3;1;-2)
Đúng 0
Bình luận (0)