tính các số hữu tỉ x,y,z biết các số đó thỏa mãn điều kiện xy=1/3 ; yz=-2/5 và xz=-3/10
NT
Những câu hỏi liên quan
Trong số các số phức z thỏa mãn điều kiện
z
-
4
+
3
i
3
gọi
z
0
là số phức có mô đun lớn nhất. Khi đó
z
0
là: A. 3 B. 4 C....
Đọc tiếp
Trong số các số phức z thỏa mãn điều kiện z - 4 + 3 i = 3 gọi z 0 là số phức có mô đun lớn nhất. Khi đó z 0 là:
A. 3
B. 4
C. 5
D. 8
Đáp án D
Cách giải: gọi z=x+yi
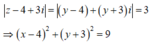
Vậy quỹ tích các điểm z thuộc đường tròn tâm I(4;-3); R=3
Đặt 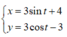
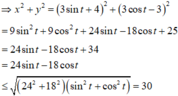
(theo bunhiacopxki)
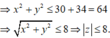
Đúng 0
Bình luận (0)
Trong số các số phức z thỏa mãn điều kiện |z-4+3i|=3, gọi z 0 là số phức có mô đun lớn nhất. Khi đó | z 0 | là:
A. 3
B. 4
C. 5
D. 8
Tìm các số hữu tỉ x, y thỏa mãn điều kiện: \(\frac{x}{7}\)=\(\frac{y}{13}\)và x - y = 42
Bài làm
Áp dụng tính chất dãy tỉ số bằng nhau, có:
\(\frac{x}{7}=\frac{y}{13}=\frac{x-y}{7-13}=\frac{42}{-6}=-7\)
Do đó:
\(\hept{\begin{cases}\frac{x}{7}=-y\\\frac{y}{13}=-7\end{cases}}\Rightarrow\hept{\begin{cases}x=-49\\y=-91\end{cases}}\)
Vậy x = -49; y = -91
Đặt \(\frac{x}{7}=\frac{y}{13}=k\)
=> x = 7k,y = 13k
=> x - y = 7k - 13k
=> x - y = -6k
=> 42 = -6k
=> k = -7
Vậy x = 7.(-7) = -49 , y = 13.(-7) = -91
Áp dụng tính chất dãy tỉ số = nhau ta có :
\(\frac{x}{7}=\frac{y}{13}=\frac{x-y}{7-13}=\frac{42}{-6}=-7\)
\(\frac{x}{7}=-7=>x=-49\)
\(\frac{y}{13}=-7=>y=-7.13=-91\)
Vậy x = -49 và y = -91
Xem thêm câu trả lời
Trong các số phức thỏa mãn điều kiện
z
-
4
i
-
2
2
i
-
z
, môđun nhỏ nhất của số phức z bằng: A.
2
B.
3
C.
2
2
D.
2
3
Đọc tiếp
Trong các số phức thỏa mãn điều kiện z - 4 i - 2 = 2 i - z , môđun nhỏ nhất của số phức z bằng:
A. 2
B. 3
C. 2 2
D. 2 3
Cho các số thực x,y,z thỏa mãn đồng thời các điều kiện \(x+y+z=2\) , \(x^2+y^2+z^2=18\)và \(xyz=-1\)
Tính giá trị của \(S=\frac{1}{xy+z-1}+\frac{1}{yz+x-1}+\frac{1}{zx+y-1}\)
Ta có \(xy+yz+xz=\frac{2^2-18}{2}=-7\)
\(x+y+z=2\)=> \(z-1=-x-y+1\)
=> \(\frac{1}{xy+z-1}=\frac{1}{xy-x-y+1}=\frac{1}{\left(x-1\right)\left(y-1\right)}\)
Tương tự \(\frac{1}{yz+x-1}=\frac{1}{\left(y-1\right)\left(z-1\right)};\frac{1}{xz+y-1}=\frac{1}{\left(z-1\right)\left(x-1\right)}\)
=> \(S=\frac{x+y+z-3}{\left(x-1\right)\left(y-1\right)\left(z-1\right)}=-\frac{1}{xyz-\left(yz+xy+xz\right)+\left(x+y+z\right)-1}\)
\(=\frac{-1}{-1+7+2-1}=-\frac{1}{7}\)
Vậy \(S=-\frac{1}{7}\)
Đúng 0
Bình luận (0)
Cho hàm số f:Z^+rightarrow R^+ thỏa mãn các điều kiện1.f_{left(xright)}0leftrightarrow x02.f_{left(xyright)}f_{left(xright)}f_{left(yright)}left(forall x,yin Z^+right)3.f_{left(x+yright)}f_{left(xright)}+f_{left(yright)}left(forall x,yin Z^+right)Gọi n_o là số nguyên dương bé nhất trong các số nguyên dương m thõa mãn điều kiện f_{left(mright)}1. Chứng minh rằng với mọi số nguyên dương n ta đều có bất đẳng thức sau : f_{left(nright)}...
Đọc tiếp
Cho hàm số \(f:Z^+\rightarrow R^+\) thỏa mãn các điều kiện
\(1.f_{\left(x\right)}=0\leftrightarrow x=0\)
\(2.f_{\left(xy\right)}=f_{\left(x\right)}f_{\left(y\right)}\left(\forall x,y\in Z^+\right)\)
\(3.f_{\left(x+y\right)}=f_{\left(x\right)}+f_{\left(y\right)}\left(\forall x,y\in Z^+\right)\)
Gọi \(n_o\) là số nguyên dương bé nhất trong các số nguyên dương m thõa mãn điều kiện \(f_{\left(m\right)}>1\). Chứng minh rằng với mọi số nguyên dương n ta đều có bất đẳng thức sau :
\(f_{\left(n\right)}< \dfrac{\left(f_{\left(n_o\right)}\right)^{1+\left[log_{n_o}n\right]}}{f_{\left(n_o\right)}-1}\)
\(\left[a\right]\) là phần nguyên của số thực \(a\)
Dùng ba chữ số 4,0,5 hãy ghép thành các số tự nhiên có ba chữ số khác nhau thỏa mãn điều kiện:
a, Số đó chia hết cho 2
b, Số đó chia hết cho 5
a) Các số lập được là:
450;504;540
b) Các số lập được là;
405;450;540
Đúng 0
Bình luận (0)
đáp án nè bn
a)số đó chia hết cho 2 là:504,540,450
b)số đó chia hết cho 5 là 504,405,540
đúng thì bn nhớ tc nhé
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho các số hữu tỉ a,b,c,d thỏa mã các điều kiện : \(a^2+b^4+c^6+d^8=1\)và \(a^{2016}+b^{2017}+c^{2018}+d^{2019}=1\)
Tính giá trị M : a^3 - a + 3b^4 -3b +5c^5 - 5c + 7d^6 - 7d
Ở link: Câu hỏi của Thị Kim Vĩnh Bùi - Toán lớp 8 - Học toán với OnlineMath
đã tìm được giá trị của a, b, c, d
Thay vào tìm M nhé!
cho x, y, z là các số dương thỏa mãn điều kiện x+ y+ z lớn hơn hoặc bằng 12
tìm GTNN của biểu thức P= x/ căn y + y/ căn z + z/ căn x




