tìm các nguyên tố x ; y sao cho x2 -2y2=1
NN
Những câu hỏi liên quan
a) Tìm các giá trị nguyên của x để phân số sau nhận các giá trị nguyên:
A= 6x +9/ 3x+2
b) Tìm giá trị nhỏ nhất của biểu thức :
A=| x | + | 8-x |
\(a)\) Ta có :
\(A=\frac{6x+9}{3x+2}=\frac{6x+4+5}{3x+2}=\frac{6x+4}{3x+2}+\frac{5}{3x+2}=\frac{2\left(3x+2\right)}{3x+2}+\frac{5}{3x+2}=2+\frac{5}{3x+2}\)
Để A có giá trị nguyên thì \(\frac{5}{3x+2}\) phải nguyên hay \(5\) chia hết cho \(3x+2\)\(\Rightarrow\)\(\left(3x+2\right)\inƯ\left(5\right)\)
Mà \(Ư\left(5\right)=\left\{1;-1;5;-5\right\}\)
Suy ra :
| \(3x+2\) | \(1\) | \(-1\) | \(5\) | \(-5\) |
| \(x\) | \(\frac{-1}{3}\) | \(-1\) | \(1\) | \(\frac{-7}{3}\) |
Mà \(x\) là số nguyên nên \(x\in\left\{-1;1\right\}\)
Vậy \(x\in\left\{-1;1\right\}\)
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
\(b)\) Ta có bất đẳng thức giá trị tuyệt đối như sau :
\(\left|x\right|+\left|y\right|\ge\left|x+y\right|\)
Dấu "=" xảy ra khi và chỉ khi \(xy\ge0\)
Áp dụng vào ta có :
\(A=\left|x\right|+\left|8-x\right|\ge\left|x+8-x\right|=\left|8\right|=8\)
Dấu "=" xảy ra khi và chỉ khi \(x\left(8-x\right)\ge0\)
Trường hợp 1 :
\(\hept{\begin{cases}x\ge0\\8-x\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge0\\x\le8\end{cases}\Leftrightarrow}0\le x\le8}\)
Trường hợp 2 :
\(\hept{\begin{cases}x\le0\\8-x\le0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le0\\x\ge8\end{cases}}}\) ( loại )
Vậy GTNN của \(A=8\) khi \(0\le x\le8\)
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
[...]5chia hết 3x+2
3x+2thuoc tập ước của 5
[...]
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm các số nguyên a,v,c,d,e,biết tổng của chúng bằng 0 và a+b=c+d=d+e=2
Tìm các số nguyên x,y,z biết x+y+z=0;x+y=3;y+z=-1
Tìm các số nguyên x:
12⋮x và 15⋮x
Vì 12 chia hết cho x và 15 chia hết cho x
=> x thuộc ƯC(12,15)
Ta có: 12 = 22 . 3
15 = 3. 5
=> ƯCLN(12,15) = 3
=> ƯC(12,15) = {-3:-1:1:3}
Đúng 1
Bình luận (0)
12⋮x và 15⋮x => x ϵ ƯC(12,15)
12 = 22.3
15 = 3.5
=> ƯCLN(12,15) = 3
=> ƯC(12,15) = Ư(3) = {-3;-1;1;3}
Đúng 0
Bình luận (0)
Ta có:
12⋮x;15⋮x
⇒xϵƯC(12;15)
ƯCLN(12;15)
Ta có:
12=22.3
15=3.5
⇒Vậy ƯCLN(12;15)=3
ƯC(12;15)={1;-1;3;-3}
❤Cho tích nhé❤
Đúng 0
Bình luận (0)
Tìm các số nguyên x thoả mãn: (x + 4) ⋮ (x + 1)
Ta có x + 4 = (x + 1) + 3
nên (x + 4) ⋮ (x + 1) khi 3 ⋮ (x + 1), tức là x + 1 là ước của 3.
Vì Ư(3) = {-1; 1; -3; 3} ta có bảng sau:

Đáp số x = -4; -2; 0; 2.
Đúng 0
Bình luận (0)
Tìm các số nguyên x biết:
(x+2) (x-1) > 0
Ta có các trường hợp:
+TH1: \(\left\{{}\begin{matrix}x+2>0\\x-1>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x>-2\\x>1\end{matrix}\right.\)\(\Leftrightarrow x>1\)
+TH2: \(\left\{{}\begin{matrix}x+2< 0\\x-1< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x< -2\\x< 1\end{matrix}\right.\)\(\Leftrightarrow x< -2\)
Vậy.....
Đúng 0
Bình luận (0)
(x+2) (x-1)>0 thì nó có cả đống bạn ạ VD:
(10+2)x(11-1)= 120 > 0
Đúng 0
Bình luận (0)
Tìm các số nguyên x biết:
(x+3) (x-2) < 0
Ta có các trường hợp sau:
+TH1: \(\left\{{}\begin{matrix}x+3>0\\x-2< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x>-3\\x< 2\end{matrix}\right.\)\(\Leftrightarrow-3< x< 2\)
+TH2: \(\left\{{}\begin{matrix}x+3< 0\\x-2>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x< -3\\x>2\end{matrix}\right.\) (vô lý)
Vậy -3<x<2
Đúng 0
Bình luận (0)
x+10 là bội của x+3 tìm các số nguyên x
Lời giải:
$x+10\vdots x+3$
$\Rightarrow (x+3)+7\vdots x+3$
$\Rightarrow 7\vdots x+3$
$\Rightarrow x+3\in \left\{\pm 1; \pm 7\right\}$
$\Rightarrow x\in \left\{-2; -4; 4; -10\right\}$
Đúng 0
Bình luận (0)
Bài 1 . Tìm các số tự nhiên n biết : 6 là bội của n + 1 .
Bài 2 . Tìm các số nguyên x sao cho 2x - 5 chia hết cho x + 1.
6 là bội của n+1
=> 6 chia hết cho n+1
=> n+1 thuộc Ư(6)={-1,-2,-3,-6,1,2,3,6}
Ta có bảng :
| n+1 | -1 | -2 | -3 | -6 | 1 | 2 | 3 | 6 |
| n | -2 | -3 | -4 | -7 | 0 | 1 | 2 | 5 |
Vậy n={-7,-4,-3,-2,0,1,2,5}
Đúng 0
Bình luận (0)
6 là bội của n+1
=> 6 chia hết cho n+1
=> n+1 thuộc Ư(6)={-1,-2,-3,-6,1,2,3,6}
Ta có bảng :
| n+1 | -1 | -2 | -3 | -6 | 1 | 2 | 3 | 6 |
| n | -2 | -3 | -4 | -7 | 0 | 1 | 2 | 5 |
Vậy n={-7,-4,-3,-2,0,1,2,5}
Đúng 0
Bình luận (0)
Tìm các số nguyên x thoả mãn: (4x + 3) ⋮ (x - 2).
Ta có 4x + 3 = 4(x - 2) + 11
nên (4x + 3) ⋮ (x - 2) khi 11 ⋮ (x - 2), tức là x -2 là ước của 11
Ư(11) = { -11; -1; 1; 11}; ta có bảng sau:
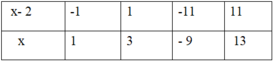
Vậy các số nguyên x thỏa mãn là: x ∈ { 1; 3; - 9; 13}
Đúng 0
Bình luận (0)


