Cho tam giác ABC đều và D là một điểm thuộc cạnh BC. Trên nửa mặt phẳng bờ BC không chứa điểm A; vẽ tia Bx sao cho góc CBx = góc CAD. Tia Bx cắt tia AD tại E. Chứng minh rằng EA = EB + EC. Mk cần gấp ! Cảm ơn trước nhé !
NM
Những câu hỏi liên quan
CHO Tam giác abc đều trên nửa mặt phẳng bờ bc không chứa điểm a vẽ nửa đường tròn đường kính bc. lấy điểm d thuộc nửa đường tròn sao cho sd CD = 60. gọi i là giao điểm ad và bc. chứng minh bi=2ci
Cho tam giác đều ABC. Gọi K là điểm thuộc cạnh AB sao cho KA 2KB. Lấy điểm O bất kỳ nằm giữa K và C (O khác K và C). Gọi M, N, P và Q lần lượt là trung điểm OA, OB, BC và AC.a) Chứng minh tứ giác MNPQ là hình bình hành.b) Trên nửa mặt phẳng bờ OB không chứa điểm C vẽ tam giác đều OBE. Trên nửa mặt phẳng bờ OC không chứa điểm B vẽ tam giác đều OCF. Chứng minh tứ giác AEOF là hình bình hành.
Đọc tiếp
Cho tam giác đều ABC. Gọi K là điểm thuộc cạnh AB sao cho KA = 2KB. Lấy điểm O bất kỳ nằm giữa K và C (O khác K và C). Gọi M, N, P và Q lần lượt là trung điểm OA, OB, BC và AC.
a) Chứng minh tứ giác MNPQ là hình bình hành.
b) Trên nửa mặt phẳng bờ OB không chứa điểm C vẽ tam giác đều OBE. Trên nửa mặt phẳng bờ OC không chứa điểm B vẽ tam giác đều OCF. Chứng minh tứ giác AEOF là hình bình hành.
1.Cho tam giác ABC cân tại A, góc A=140°. Trên nửa mặt phẳng bờ BC chứa điểm A. Kẻ Cx sao cho góc ACx=110°. Gọi D là giao điểm của các tia Cx và BA. Trên nửa mặt phẳng bờ BC chứa điểm A dựng tam giác BCE đều. CMR: AB=BC
¿¿¿ Mọi người giúp mk nha ¿¿¿
Cho tam giác ABC. Trên nửa mặt phẳng bờ AB không chứa điểm C vẽ và AF = AB, trên nửa mặt phẳng bờ AC không chứa điểm B vẽ và AH = AC. Gọi D là trung điểm của cạnh BC, I là một điểm trên tia đối của tia DA sao cho DI = DA. Chứng minh:
a) AI = FH;
b) DA vuông góc với FH.
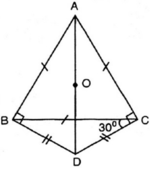
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và D C B ^ = 1 2 A C B ^ . Chứng minh tứ giác ABDC là tứ giác nội tiếp.
Do tam giác ABC là tam giác nên A C B ^ = 60 o
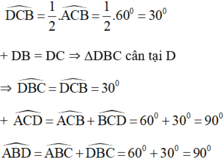
=> Tứ giác ABDC có: ![]()
=> ABDC là tứ giác nội tiếp
Đúng 0
Bình luận (0)
cho tam giác ABC vuông ở A trên nữa mặt phẳng bờ BC chứa đingr A kẻ Bx vuông BC, lấy điểm D thuộc BC sao cho DB= BC. Trên nửa mặt phẳng bờ AB không chứa C kẻ BI vuông Ab từ điểm D kẻ DE vuông BI ( e thuộc BI )
a) cm tam giác EBD = tam giác ABC
b) cm tam giác EBA vuông cân
c) cm AC=DE
cho tam giác ABC đều và D là một điểm thuộc cạnh BC.Trên nửa mặt phẳng bờ BC không chứ điểm A;Vẽ tia Bx sao cho CBx=CAD.Tia Bx cắt tia AD tại E.Chứng minh rằng EA=EB+EC
cho tam giác ABC trên mặt phẳng có bờ chứa cạnh AB vẽ tam giác đều OAB. Trên mặt phẳng có chứa bờ BC vẽ tam giác đều BEC. Gọi N, D,M lần lượt là trung điểm củaOB,AC,BC . CMR NMD là tam giác đều
Câu 4 (3,5 điểm): Cho tam giác ABC, gọi D là trung điểm của BC, vẽ DE // BC (E thuộc cạnh AC). Vẽ EF || AB (F thuộc cạnh BC)
| a) Chứng minh ADE = EFC
b) Vẽ góc CE, sao cho CTy = BCE (tia Ey nằm trên nửa mặt phẳng bờ AC không chứa B). Chứng minh Dy // BC
c) So sánh diện tích hình thang DECB với diện tích tam giác ABC.
vẽ hình được thì càng tốt ạ. em camon

