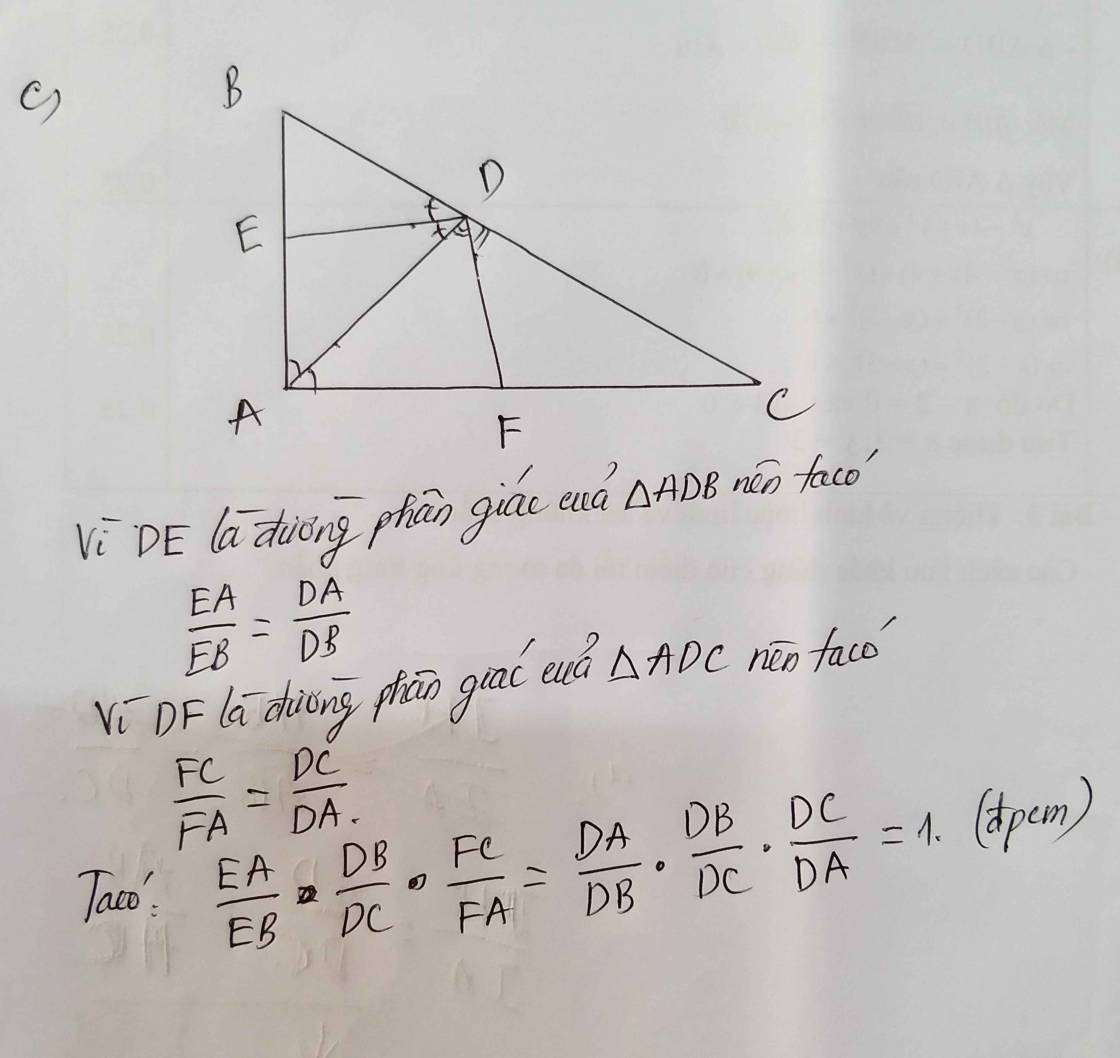
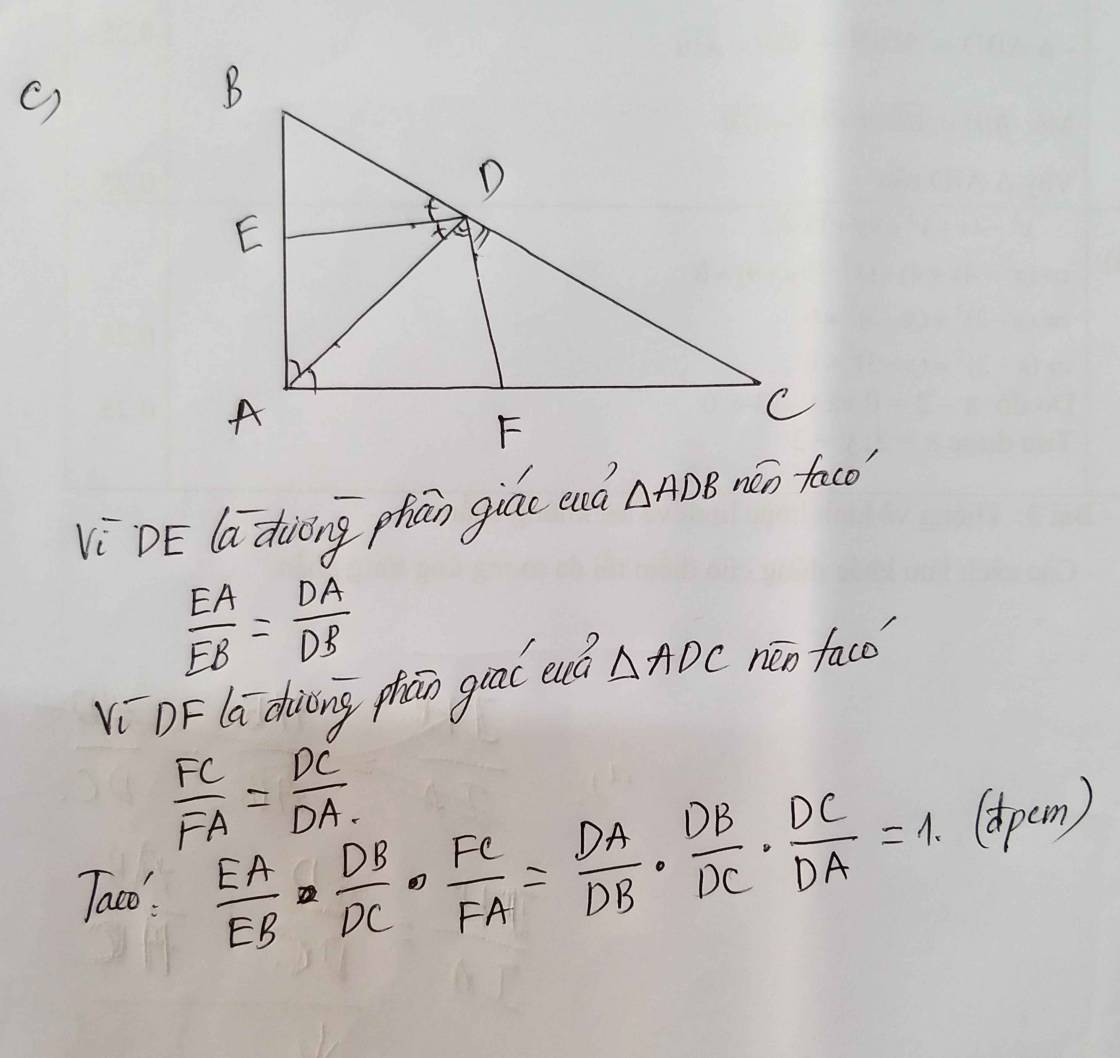
Trong tam giác ABC có AB=AC>BC ; góc BAC có số đo là 500. Từ B kẻ BH vuông góc với AC tại H, từ C kẻ CK vuông góc với AB tại K
a) Chứng minh tam giác ABH bằng tam giác ACK và BH = CK
b) Gọi O là giao điểm của BH và CK. Tính số đo góc BOC
c) Cho M là trung điểm của BC. Chứng minh BC=2MK