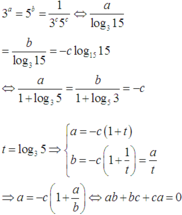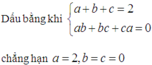Đáp án B

\(\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+d}+\dfrac{d}{d+a}=2\)

\(1-\dfrac{a}{a+b}-\dfrac{b}{b+c}+1-\dfrac{c}{c+d}-\dfrac{d}{d+a}=0\)

\(\dfrac{b}{a+b}-\dfrac{b}{b+c}+\dfrac{d}{c+d}-\dfrac{d}{d+a}=0\)

\(\dfrac{b\left(c-a\right)}{\left(a+b\right)\left(b+c\right)}+\dfrac{d\left(a-c\right)}{\left(c+d\right)\left(d+a\right)}=0\)

<=>b(c+d)(d+a)+d(a+b)(b+c)=0 (vì c≠a)

<=>abc-acd+bd²-b²d=0

<=> (b-d)(ac-bd)=0 <=> ac - bd =0 (vì b≠d) <=> ac = bd

Vậy abcd =(ac)(bd)=(ac)²

Up ba, giải giúp mik dới !!!!!!!!!

\(b^2=ac\Rightarrow\dfrac{a}{b}=\dfrac{b}{c};c^2=bd\Rightarrow\dfrac{b}{c}=\dfrac{c}{d}\\ \Rightarrow\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\\ \Rightarrow\dfrac{a^3}{b^3}=\dfrac{b^3}{c^3}=\dfrac{c^3}{d^3}=\dfrac{a^3+b^3+c^3}{c^3+b^3+d^3}\left(1\right)\\ \text{Đặt }\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=k\\ \Rightarrow a=bk;b=ck;c=dk\\ \Rightarrow a=bk=ck^2=dk^3\\ \Rightarrow\dfrac{a}{d}=k^3\\ \text{Mà }\dfrac{a}{b}=k\Rightarrow\dfrac{a^3}{b^3}=k^3\\ \Rightarrow\dfrac{a}{d}=\dfrac{a^3}{b^3}\left(2\right)\\ \left(1\right)\left(2\right)\RightarrowĐpcm\)

Đáp án B

3 a = 5 b = 1 3 c 5 c ⇔ a log 3 15 = b log 3 15 = - c log 15 15 ⇔ a 1 + log 3 5 = b 1 + log 5 3 = - c

Đặt  t = log 3 5 ⇒ a = - c 1 + t b = - c 1 + 1 t = a t ⇒ a = - c 1 + a b ⇔ a b + b c + c a = 0

⇒ P = a + b + c 2 - 4 a + b + c ≥ - 4 . Dấu bằng khi a + b + c = 2 a b + b c + c a = 0 , chẳng hạn a = 2,b = c = 0.

Ai giúp gấp nhé:D

Ta có : a² + b² = c² + d²

a² + b² + c² + d² = 2 ( a² + b² ) ⋮2 nên là hợp số

Ta có : a² + b² + c² + d² - ( a + b + c + d ) 

= a ( a - 1 ) + b ( b - 1 ) + c ( c - 1 ) + d ( d - 1 ) ⋮2

a + b + c + d ⋮2 nên cũng là hợp số

Ta có: \(a^2+b^2=c^2+d^2\)

\(\Rightarrow a^2+b^2+a^2+b^2=a^2+b^2+c^2+d^2\)

\(\Rightarrow2\left(a^2+b^2\right)=a^2+b^2+c^2+d^2\)

\(\Rightarrow a^2+b^2+c^2+d^2\) là chẵn

Xét hiệu: \(a^2+b^2+c^2+d^2-a-b-c-d=a\left(a-1\right)+b\left(b-1\right)+c\left(c-1\right)+d\left(d-1\right)\)

Mà tích 2 số TN liên tiếp là chẵn

⇒ Tổng a+b+c+d là chẵn

Vì \(a+b+c+d>2\) với mọi số TN a,b,c,d khác 0

⇒ a+b+c+d là hợp số

ta có câu hỏi sau

giúp mình với nha các bạn

\(b^2\)= \(ac\)=> \(\frac{a}{b}\)= \(\frac{b}{c}\)(1)

\(c^2\)= \(bd\)=> \(\frac{b}{c}\)= \(\frac{c}{d}\)(2)

từ (1) và (2) => \(\frac{a}{b}\)= \(\frac{b}{c}\)= \(\frac{c}{d}\)=> \(\frac{a^3}{b^3}\)= \(\frac{c^3}{d^3}\)= \(\frac{b^3}{c^3}\)=> \(\frac{a^3}{b^3}\)= \(\frac{a}{b}\)*   \(\frac{b}{c}\)*   \(\frac{c}{d}\)= \(\frac{a}{d}\)         (*)

\(\frac{a^3}{b^3}\)=   \(\frac{b^3}{c^3}\)=  \(\frac{c^3}{d^3}\)=   \(\frac{a^3+b^3+c^3}{b^3+c^3+d^3}\)            (**)

Từ (*) và (**) => \(\frac{a}{d}\)= \(\frac{a^3+b^3+c^3}{b^3+c^3+d^3}\)  (đpcm)

A=2 

C=4