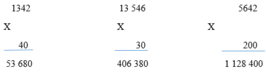Đặt $ X = a - b; Y = b - c; Z = c - a \Rightarrow X + Y + Z = 0$
Với X + Y + Z = 0, ta chứng minh được :
$ ( \dfrac{1}{X} + \dfrac{1}{Y} + \dfrac{1}{Z} )^2 = \dfrac{1}{X^2} + \dfrac{1}{Y^2} + \dfrac{1}{Z^2}$
Thật vậy, ta có :
$ ( \dfrac{1}{X} + \dfrac{1}{Y} + \dfrac{1}{Z} )^2 = \dfrac{1}{X^2} + \dfrac{1}{Y^2} + \dfrac{1}{Z^2} + \dfrac{2}{XY} + \dfrac{2}{YZ} + \dfrac{2}{ZX}$
$ = \dfrac{1}{X^2} + \dfrac{1}{Y^2} + \dfrac{1}{Z^2} + 2.\dfrac{X + Y + Z}{XYZ}$
$ = \dfrac{1}{X^2} + \dfrac{1}{Y^2} + \dfrac{1}{Z^2}$ ( do X + Y + Z = 0)
$ \Rightarrow \sqrt{\dfrac{1}{X^2} + \dfrac{1}{Y^2} + \dfrac{1}{Z^2}} = \sqrt{( \dfrac{1}{X} + \dfrac{1}{Y} + \dfrac{1}{Z} )^2} = |\dfrac{1}{X} + \dfrac{1}{Y} + \dfrac{1}{Z}|$
Suy ra : $ \sqrt{\dfrac{1}{(a - b)^2} + \dfrac{1}{(b - c)^2} +\dfrac{1}{( c - a)^2}} = |\dfrac{1}{a - b} + \dfrac{1}{b - c} + \dfrac{1}{c - a}|$
Do a, b, c là số hữu tỷ nên $|\dfrac{1}{a - b} + \dfrac{1}{b - c} + \dfrac{1}{c - a}|$ cũng là số hữu tỷ. Ta có điều phải chứng minh.
NA
Những câu hỏi liên quan
Bài 13: Đặt tính rồi tính:
a) 351: 54 b) 8,46 : 3,6 c) 204,48 : 48
a) 72,85 x 32 b) 35,48 x 4,8 c) 21,83 x 4,05
Đặt tính ra luôn nhé !
bài 1 Đặt tính rồi tính a 245 x 308 b 1740 x 136 C 37460 : 682 B 57150 : 127 phải đặt phép tính cơ
a) 75460
b) 236640
c) 54,92
d) 450
Vì ko đặt tính đc nên ra kết quả luôn
Đúng 1
Bình luận (0)
a) 75460
b) 236640
c) 54,92
d) 450,23
Vì ko đặt tính đc nên ra kết quả luôn
Đúng 1
Bình luận (0)
3. Đặt tính rồi tính
a) 784,28 + 57,265 b) 625,3 – 96,754 c) 38,79 x 4,6 d) 18 : 14,4
4. Đặt tính rồi tính:
a) 436,438 + 82,137 b) 85,24 – 52,456 c) 64,2 x 43 d) 119,7 : 38
5. Đặt tính rồi tính :
a) 252,875 + 654,92 b) 653,24 – 68,125 c) 0,852 x 6,4 d)126 : 45
ê sao dài thế chẳng ra đâu vào đâu cả
Đúng 0
Bình luận (0)
Đặt x = \(\frac{a-b}{a+b}\), y = \(\frac{b-c}{b+c}\), z = \(\frac{c-a}{c+a}\)
Chứng minh x + y + z + xyz =0
Đặt x = \(\frac{a-b}{a+b}\), y = \(\frac{b-c}{b+c}\), z = \(\frac{c-a}{c+a}\)
Chứng minh x + y + z + xyz =0
Lời giải:
Nếu $x=0$ thì $a=b$. Khi đó:
$x+y+z+xyz=y+z=\frac{b-c}{b+c}+\frac{c-b}{c+b}=0$ (đpcm)
Tương tự: $y=0; z=0$ cũng vậy.
Nếu $xyz\neq 0$:
\(\frac{1}{xy}+\frac{1}{yz}+\frac{1}{xz}=\frac{(a+b)(b+c)}{(a-b)(b-c)}+\frac{(b+c)(c+a)}{(b-c)(c-a)}+\frac{(a+b)(a+c)}{(a-b)(c-a)}\)
\(=\frac{(a+b)(b+c)(c-a)+(b+c)(c+a)(a-b)+(a+b)(a+c)(b-c)}{(a-b)(b-c)(c-a)}\)
\(=\frac{(ab+bc+ac)[(c-a)+(b-c)+(a-b)]+b^2(c-a)+c^2(a-b)+a^2(b-c)}{(a-b)(b-c)(c-a)}\)
\(=\frac{b^2(c-a)+c^2(a-b)+a^2(b-c)}{(a-b)(b-c)(c-a)}=\frac{(a^2b+b^2c+c^2a)-(ab^2+bc^2+ca^2)}{(ab^2+bc^2+ca^2)-(a^2b+b^2c+c^2a)}=-1\)
\(\Rightarrow \frac{1}{xy}+\frac{1}{yz}+\frac{1}{xz}+1=0\Leftrightarrow \frac{x+y+z+xyz}{xyz}=0\Rightarrow x+y+z+xyz=0\)
Ta có đpcm.
Đúng 0
Bình luận (0)
Đặt
a
2
X
,
b
3
y
Hãy biểu diễn
M
2
x
3
.
3
1
y
2
qua a, b, x, y.
Đọc tiếp
Đặt a = 2 X , b = 3 y Hãy biểu diễn M = 2 x 3 . 3 1 y 2 qua a, b, x, y.
![]()
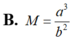
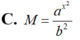
![]()
Tìm a và b để đa thức A chia hết cho đa thức B:
a) A=x3 + ax2 + 2x +b; B=x2 + 2x+3
b) A= x4 - 3x3 + bx2 + ax +b; B= x2 -1
Đặt phép chia nha chứ kh phải đặt hàng ngang nha
a) Mình không rảnh đặt phép chia, hệ số bất định vậy.
Giả sử khi A chia hết cho B thì sẽ được thương là x+c
\(\Rightarrow A=B\left(x+c\right)\)
\(\Leftrightarrow x^3+ax^2+2x+b=\left(x^2+2x+3\right)\left(x+c\right)\)
\(\Leftrightarrow x^3+ax^2+2x+b=x^3+\left(2+c\right)x^2+\left(3+2c\right)x+3c\)
\(\Leftrightarrow\hept{\begin{cases}a=2+c\\2=3+2c\\b=3c\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}a=\frac{3}{2}\\b=\frac{-3}{2}\\c=\frac{-1}{2}\end{cases}}\)
KL: \(a=\frac{3}{2};b=\frac{-3}{2}\)
b) Giải tương tự.
Đặt tính rồi tính: a) 658,3 + 96,28 b) 288 – 93,36 c) 67,28 x 5,3 d) 9,204 x 8,2 e) 18 : 0,24 g) 18,5 : 7,4 đặt tính giúp
A=\(\dfrac{x-1}{x^2}\)B=\(\dfrac{x-1}{2x+1}\)
Đặt C=A:B
\(C=\dfrac{x-1}{x^2}:\dfrac{x-1}{2x+1}\)
\(C=\dfrac{x-1}{x^2}.\dfrac{2x+1}{x-1}\)
\(C=\dfrac{2x+1}{x^2}\)
Đúng 1
Bình luận (0)
Đặt tính rồi tính
a) 1324 x 40;
b) 13546 x 30;
c) 5642 x 200.
kết quả:
a.53680
b.406380
c.1128400
Đúng 0
Bình luận (0)