Cho hình chóp S.ABC có AB = 6a, AC = 4a; SA = SB = SC = BC = 5a. Tính thể tích V khối chóp S.ABC theo a
A. 5 a 3 111 4
B. 15 a 3 111 4
C. 5 a 3 111 12
D. 45 a 3 111 4
PB
Những câu hỏi liên quan
Cho hình chóp S.ABC có
A
B
6
a
;
A
C
4
a
;
S
A
S
B
S
C
B
C
5
a
.
Tính thể tích V khối chóp S.ABC theo A.
V
5
a
3
111...
Đọc tiếp
Cho hình chóp S.ABC có A B = 6 a ; A C = 4 a ; S A = S B = S C = B C = 5 a . Tính thể tích
V khối chóp S.ABC theo
A. V = 5 a 3 111 4
B. V = 15 a 3 111 4
C. V = 5 a 3 111 12
D. V = 45 a 3 111 4
Đáp án A
Gọi H là hình chiếu của S lên (ABC) suy ra H là tâm đường tròn ngoại tiếp tam giác ABC
Áp dụng công thức Hê – rông, tính được S A B C = 15 a 2 7 4
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, cạnh bên SA vuông góc với mặt đáy, biết AB4a, SB6a. Thể tích khối chóp S.ABC là V. Tỷ số
a
3
3
V
có: A.
5
80
B.
5
40
C....
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, cạnh bên SA vuông góc với mặt đáy, biết AB=4a, SB=6a. Thể tích khối chóp S.ABC là V. Tỷ số a 3 3 V có:
A. 5 80
B. 5 40
C. 5 20
D. 3 5 80
Chọn B.
Do ∆ ABC vuông cân tại C và AB=4a nên có diện tích là: S A B C = 4 a 2
SA vuông góc với đáy nên ∆ SAB vuông tại A suy ra S A = S B 2 - A B 2 = 2 a 5
Thể tích khối chóp S.ABC là: V = 1 3 . S A . S A B C = 1 3 8 a 3 5
Vậy a 3 3 V = 5 40 . Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, cạnh bên SA vuông góc với mặt đáy, biết AB4a, SB6a. Thể tích khối chóp S.ABC là V. Tỷ số
a
3
3
V
có: A.
5
80
B.
5
40
C.
5
20
D.
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, cạnh bên SA vuông góc với mặt đáy, biết AB=4a, SB=6a. Thể tích khối chóp S.ABC là V. Tỷ số a 3 3 V có:
A. 5 80
B. 5 40
C. 5 20
D. 3 5 80
Cho hình chóp S.ABC có SA vuông góc với (ABC) tam giác ABC vuông tại A, AB=3a,AC=4a,SA=4a. Thể tích khối chóp S.ABC là:
A. 2 a 3
B. 6 a 3
C. 8 a 3
D. 9 a 3
Cho hình chóp S.ABC có SA
⊥
(ABC), ABC là tam giác vuông tại A, AB3a; AC4a; SA5a. Tìm bán kính mặt cầu mặt cầu ngoại tiếp hình chóp S.ABC?
Đọc tiếp
Cho hình chóp S.ABC có SA ⊥ (ABC), ABC là tam giác vuông tại A, AB=3a; AC=4a; SA=5a. Tìm bán kính mặt cầu mặt cầu ngoại tiếp hình chóp S.ABC?
Cho hình chóp S.ABCD có AB3a, AC4a, BC5a, SASBSC6a.Tính thể tích V của khối chóp S.ABC? A.
V
119
a
3
B.
V
119
3
a
3
C.
V...
Đọc tiếp
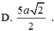
Cho hình chóp S.ABCD có AB=3a, AC=4a, BC=5a, SA=SB=SC=6a.Tính thể tích V của khối chóp S.ABC?
A. V = 119 a 3
B. V = 119 3 a 3
C. V = 4 119 3 a 3
D. V = 4 119 a 3
Đáp án A
Hướng dẫn giải:
Vì AB = 3a,AC = 4a, BC = 5a nên tam giác ABC vuông tại A.
Gọi H là hình chiếu của S lên mặt phẳng (ABC)
Vì SA = SB =SC nên H là tâm đường tròn ngoại tiếp tam giác ABC và chính là trung điểm của BC.
Do đó S H = S B 2 - H B 2 = 119 a 2 .
Diện tích tam giác ABC là S ∆ A B C = 6 a 2 .
Kết luận thể tích khối chóp
V S . A B C = 1 3 . 6 a 2 . 113 2 a = a 3 119
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC). Biết SA 2a và tam giác ABC vuông tại A có
AB
3
a
,
AC
4
a
.
Tính thể tích khối chóp S.ABC theo a A.
12
a
3
B.
6
a
3
C.
8
a
3
D. ...
Đọc tiếp
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC). Biết SA = 2a và tam giác ABC vuông tại A có AB = 3 a , AC = 4 a . Tính thể tích khối chóp S.ABC theo a
A. 12 a 3
B. 6 a 3
C. 8 a 3
D. 4 a 3
Cho hình chóp S.ABC có AB 2a, AC 4a, BC3a. Gọi H là hình chiếu của S nằm trong tam giác ABC. Các mặt bên tạo với đáy một góc
45
o
. Tính thể tích khối chóp S.ABC. A.
V
15
a
3
6
B.
V
3
15
a...
Đọc tiếp
Cho hình chóp S.ABC có AB= 2a, AC= 4a, BC=3a. Gọi H là hình chiếu của S nằm trong tam giác ABC. Các mặt bên tạo với đáy một góc 45 o . Tính thể tích khối chóp S.ABC.
A. V = 15 a 3 6
B. V = 3 15 a 3 4
C. V = 15 a 3 8
D. V = 5 a 3 8
Đáp án D
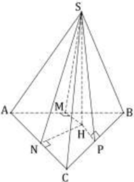
Theo giả thiết, các mặt bên tạo với đáy một góc 45 độ nên hình chiếu vuông góc của S trên (ABC) chính là tâm đường tròn nội tiếp tam giác ABC hay H là tâm đường tròn nội tiếp tam giác ABC.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có AB 2a, AC 4a, BC 3a. Gọi H là hình chiếu của S nằm trong tam giác ABC. Các mặt bên tạo với đáy một góc
45
°
. Tính thể tích khối chóp S.ABC. A.
V
15
a
3
6
.
B.
V
3...
Đọc tiếp
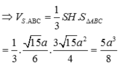
Cho hình chóp S.ABC có AB = 2a, AC = 4a, BC = 3a. Gọi H là hình chiếu của S nằm trong tam giác ABC. Các mặt bên tạo với đáy một góc 45 ° . Tính thể tích khối chóp S.ABC.
A. V = 15 a 3 6 .
B. V = 3 15 a 3 4 .
C. V = 15 a 3 8 .
D. V = 5 a 3 8 .
Đáp án D
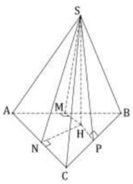
Theo giả thiết, các mặt bên tạo với đáy một góc 45 ° nên hình chiếu vuông góc của S trên (ABC) chính là tâm đường tròn nội tiếp ΔABC hay H là tâm đường tròn nội tiếp ΔABC .
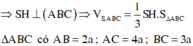
Áp dụng công thức Hê-rông em tính được p = 9 a 2 và S ΔABC = 3 15 a 2 4 .
Em lại có: S ΔABC = p . r với r là bán kính đường tròn nội tiếp tam giác ABC.
Từ H, em kẻ HM, HN, HP lần lượt vuông góc với AB, AC, BC thì
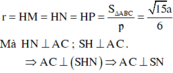
=> Góc giữa (SAC) và (ABC) chính là góc giữa SN và HN hay SNH ⏜ = 45 °
Đúng 0
Bình luận (0)