Gọi d là khoảng cách hai tâm của hai đường tròn (O; R) và (O', r) (0 < r < R). Để (O) và (O') cắt nhau thì:
A. R – r < d < R + r
B. d = R – r
C. d > R + r
D. d = R + r
PB
Những câu hỏi liên quan
Gọi d là khoảng cách hai tâm của hai đường tròn (O, R) và (O', r) (với 0 < r < R). Để (O) và (O') ở ngoài nhau thì
A. d < R – r
C. d = R + r
B. d = R – r
D. d > R + r
cho đường tròn (O;R) và đường thẳng a ở ngoài đường thẳng a ở ngoài đường tròn. Gọi OH là khoảng cách từ tâm O đếna và M là một điểm chuyển động trên a. Từ M kẻ hai tiếp tuyến MA,MB với đường tròn (O) , (A,B là 2 tiếp điểm). Gọi D là giao điểm của AB với OH.CMR D là điểm cố định
Trả lời :
Bn Nguyễn Tũn bảo dễ ẹt thì làm đi.
- Hok tốt !
^_^
dễ ẹc thì lm cho mk coi đi
mk ko bt lm
Cho đường tròn (O,R) và điểm M cách tâm O một khoảng bằng 3R. Từ M kẻ hai đường thẳng tiếp xúc với đường tròn (O , R) tại A và B, gọi I và E là trung điểm của MA và MB. Tính khoảng cách từ O đến IE.
làm ơn giúp mình mai mình đi học rồi
Đúng 0
Bình luận (0)
cho đường tròn(o) bán kính R6cm và một điểm A cách O khoảng 10cm. Từ A vẽ tiếp tuyến AB(B là tiếp điểm) với đường tròn tâm O. lấy điểm C trên đường tròn tâm O, tia AC cắt đường tròn tâm O tại điểm thứ hai là D. gọi I là trung điểm của CDa/ tính độ dài đoạn thẳng ABb/ khi C di chuyển trên đường tròn(o) thì I di chuyển trên đường nào?c/ cm rằng tích AC.AD khồng đổi khi c thay đổi trên (o)
Đọc tiếp
cho đường tròn(o) bán kính R=6cm và một điểm A cách O khoảng 10cm. Từ A vẽ tiếp tuyến AB(B là tiếp điểm) với đường tròn tâm O. lấy điểm C trên đường tròn tâm O, tia AC cắt đường tròn tâm O tại điểm thứ hai là D. gọi I là trung điểm của CD
a/ tính độ dài đoạn thẳng AB
b/ khi C di chuyển trên đường tròn(o) thì I di chuyển trên đường nào?
c/ cm rằng tích AC.AD khồng đổi khi c thay đổi trên (o)
Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao h r
2
. Gọi A là một điểm trên đường tròn tâm O và B là một điểm trên đường tròn tâm O’ sao cho OA vuông góc với O’B. Gọi (
α
) là mặt phẳng qua AB và song song với OO’. Tính khoảng cách giữa trục OO’ và mặt phẳng (α).
Đọc tiếp
Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao h = r 2 . Gọi A là một điểm trên đường tròn tâm O và B là một điểm trên đường tròn tâm O’ sao cho OA vuông góc với O’B. Gọi ( α ) là mặt phẳng qua AB và song song với OO’. Tính khoảng cách giữa trục OO’ và mặt phẳng (α).
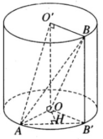
Ta có ( α ) là (ABB’). Vì OO’ // ( α ) nên khoảng cách giữa OO’ và ( α ) bằng khoảng cách từ O đến ( α ). Dựng OH ⊥ AB′ ta có OH ⊥ ( α ).
Vậy khoảng cách cần tìm là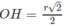 
Đúng 0
Bình luận (0)
Cho hình trụ có chiều cao
h
a
3
, bán kính đáy
r
a
. Gọi O, O lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai đường thẳng AB và OO chéo nhau và góc giữa hai đường thẳng AB và OO bằng
30
°
. Khoảng cách giữa hai đường thẳng AB và OO bằng: A.
a
6...
Đọc tiếp
Cho hình trụ có chiều cao h = a 3 , bán kính đáy r = a . Gọi O, O' lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai đường thẳng AB và OO' chéo nhau và góc giữa hai đường thẳng AB và OO' bằng 30 ° . Khoảng cách giữa hai đường thẳng AB và OO' bằng:
A. a 6 2 .
B. a 3 .
C. a 3 2
D. a 6 .
Cho hình trụ có chiều cao h a
3
, bán kính đáy r a. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng 300. Khoảng cách giữa hai đường thẳng AB và OO’ bằng : A.
a
6
B.
a
6...
Đọc tiếp
Cho hình trụ có chiều cao h = a 3 , bán kính đáy r = a. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng 300. Khoảng cách giữa hai đường thẳng AB và OO’ bằng :
A. a 6
B. a 6 2
C. a 3
D. a 3 2
Đáp án D.
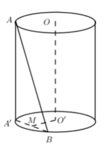
Phương pháp :
+) Xác định mặt phẳng (P) chứa AB và song song với OO’.
+) d(OO’;AB) = D(OO’;(P))
Cách giải :
Dựng AA’//OO’ ta có: (OO’;AB) = (AA’;AB) = A’AB = 300
Gọi M là trung điểm của A’B ta có:
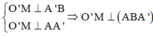
=>d(OO’;AB) = d(OO’;(ABA’)) = d(O’;(ABA’)) = O’M
Xét tam giác vuông ABA’ có 
Xét tam giác vuông O’MB có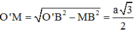 
Đúng 0
Bình luận (0)
Cho hình trụ có chiều cao ha
3
bán kính đáy ra. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng
30
0
. Khoảng cách giữa hai đường thẳng AB và OO’ bằng :
Đọc tiếp
Cho hình trụ có chiều cao h=a 3 bán kính đáy r=a. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng 30 0 . Khoảng cách giữa hai đường thẳng AB và OO’ bằng :
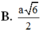
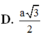
a) Vẽ đường tròn tâm O bán kính R = 2cm.
b) Vẽ một lục giác đều ABCDEF có tất cả các đỉnh nằm trên đường tròn (O).
c) Vì sao tâm O cách đều các cạnh của lục giác đều ? Gọi khoảng cách này là r.
d) Vẽ đường tròn (O; r).
a)
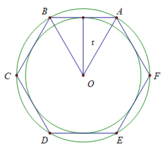
b) Cách vẽ lục giác đều có tất cả các đỉnh nằm trên đường tròn (O)
Vẽ các dây cung AB = BC = CD = DE = EF = FA = R = 2 cm
(Ta đã nêu được cách chia đường tròn thành sáu cung bằng nhau tại bài tập 10 SGK trang 71)
c) Vì các dây cung AB = BC = CD = DE = EF = FA bằng nhau nên khoảng cách từ O đến các dây là bằng nhau ( định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây)
Đúng 0
Bình luận (0)