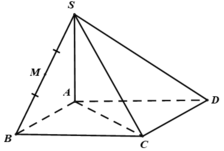
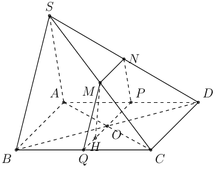
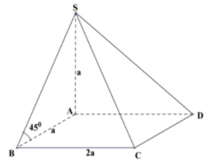
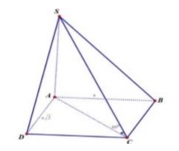
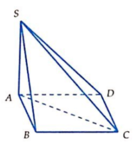
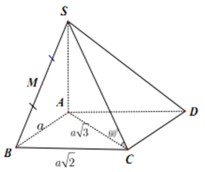
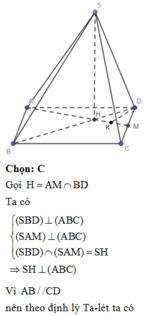
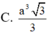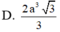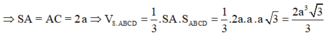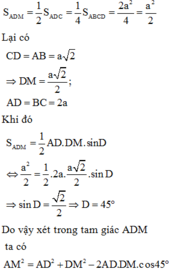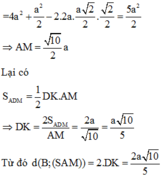Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng 2 a 2 , AB = a 2 ; BC = 2a. Gọi M là trung điểm của DC. Hai mặt phẳng (SBD) và (SAM) cùng vuông góc với đáy. Khoảng cách từ điểm B đến mặt phẳng (SAM) bằng
A. 4 a 10 15
B. 3 a 10 5
C. 2 a 10 5
D. 3 a 10 15