Cho hai đa thức P(x) và Q(x). Xét các tập hợp sau:
A = { x ∈ ℝ : P ( x ) = 0 } ; B = { x ∈ ℝ : Q ( x ) = 0 } ; C = x ∈ ℝ : P ( x ) 2 + Q ( x ) 2 = 0
Trong các mệnh đề sau, mệnh đề nào đúng?
A. C = A ∪ B
B. C = A ∩ B
C. C = A \ B
D. C = B \ A
Cho hai đa thức P(x) và Q(x). Xét các tập hợp sau:
A = { x ∈ ℝ : P ( x ) = 0 } ; B = { x ∈ ℝ : Q ( x ) = 0 } ; C = x ∈ ℝ : P ( x ) Q ( x ) = 0
Trong các mệnh đề sau, mệnh đề nào đúng?
A. C = A ∩ B
B. C = A ∪ B
C. C = A \ B
D. C = B \ A
Cho hai đa thức P(x) và Q(x). Xét các tập hợp sau:
A = { x ∈ ℝ : P ( x ) = 0 } ; B = { x ∈ ℝ : Q ( x ) = 0 } ; C = x ∈ ℝ : P ( x ) . Q ( x ) = 0 .
Trong các mệnh đề sau, mệnh đề nào đúng?
A. C = A \ B
B. C = B \ A
C. C = A ∩ B
D. C = A ∪ B
Cho hai đa thức f(x) và g(x). Xét các tập hợp:
A = x ∈ R f ( x ) = 0 ; B = x ∈ R g ( x ) = 0 ; C = x ∈ R f 2 ( x ) + g 2 ( x ) = 0
Trong các mệnh đề sau, mệnh đề nào đúng?
A. C = A ∪ B
B. C = A ∩ B
C. C = A\ B
D. C = B\ A
Đáp án B
Ta có:
C = x ∈ R f 2 ( x ) + g 2 ( x ) = 0 ⇒ C = x ∈ R f ( x ) = 0 , g ( x ) = 0 = A ∩ B
Cho hai đa thức f(x) và g(x) . Xét các tập hợp:
A = x ∈ R f ( x ) = 0 B = x ∈ R g ( x ) = 0 C = x ∈ R f ( x ) g ( x ) = 0
Trong các mệnh đề sau, mệnh đề nào đúng?
A. C = A ∪ B
B. C = A
C. C = A\ B
D. C = B\ A
Đáp án C
Ta có:
C = x ∈ R f ( x ) g ( x ) = 0 = x ∈ R f ( x ) = 0 , g ( x ) ≠ 0
Do đó C = A\ B
Cho hai đa thức f(x) và g(x). Xét các tập hợp A={x∈R, f(x)=0}, B={x∈R,g(x)=0}, C={x∈R,f(x)g(x)=0 } . Mệnh đề nào đúng và giải thích:
A. A hợp B
B. A giao B
C. A/B
D. B/A
Cho hai đa thức f(x) và g(x). Xét các tập hợp A={x∈R, f(x)=0}, B={x∈R,g(x)=0}, C={x∈R,\(\frac{f\left(x\right)}{g\left(x\right)}\)=0}. Mệnh đề nào đúng và giải thích:
A. C= A hợp B
B. C=A giao B
C. C=A/B
D. C=B/A
Cho hai đa thức f(x) và g(x). Xét các tập hợp A={x∈R, f(x)=0}, B={x∈R,g(x)=0}, C={x∈R,f2(x)+g2(x)=0}. Mệnh đề nào đúng và giải thích:
A. C= A hợp B
B. C=A giao B
C. C=A/B
D. C=B/A
Cho các tập hợp:
M = { x ∈ ℝ : x ≥ − 3 } , N = { x ∈ ℝ : − 2 ≤ x ≤ 1 } , P = { x ∈ ℝ : − 5 < x ≤ 0 } .
Mệnh đề nào sau đây là mệnh đề đúng?
A. M ⊂ N
B. M ⊃ P
C. N ⊂ M
D. N ⊂ P
Đáp án C.
Giải thích
M = x ∈ R : x ≥ - 3 = [ - 3 ; + ∞ ) N = x ∈ R : - 2 ≤ x ≤ 1 = [ - 2 ; 1 ] P = x ∈ R : - 5 < x ≤ 0 = ( - 5 ; 0 ]
Ta thấy rằng - 2 ; 1 ⊂ [ - 3 ; + ∞ ) d o đ ó N ⊂ M
Cho hai đa thức:
\(P(x) = 4{x^2} + 1 + 3x\) và \(Q(x) = 5x + 2{x^2} + 3\).
a) Sắp xếp các đa thức P(x), Q(x) theo số mũ giảm dần của biến.
b) Tìm đơn thức thích hợp trong dạng thu gọn của P(x) và Q(x) cho ? ở bảng sau rồi trừ hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
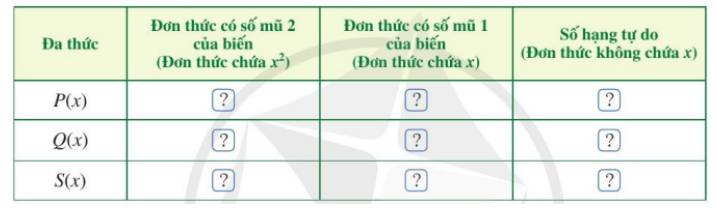
c) Dựa vào kết quả trừ hai đơn thức theo từng cột, xác định đơn thức S(x).
a) \(P(x) = 4{x^2} + 1 + 3x = 4{x^2} + 3x + 1\) ; \(Q(x) = 5x + 2{x^2} + 3 = 2{x^2} + 5x + 3\).
b)
Đa thức | Đơn thức có số mũ 2 của biến (Đơn thức chứa \({x^2}\)) | Đơn thức có số mũ 1 của biến (Đơn thức chứa x) | Số hạng tự do (Đơn thức không chứa x) |
P(x) | \(4{x^2}\) | 3x | 1 |
Q(x) | \(2{x^2}\) | 5x | 3 |
S(x) | \(2{x^2}\) | – 2x | – 2 |
c) Vậy \(S(x) = 2{x^2} - 2x - 2\)