Cho hàm số y=f(x) xác định và liên tục trên đoạn 0 ; 7 2 có đồ thị hàm số y=f '(x) như hình vẽ. Hỏi hàm số y=f(x) đạt giá trị nhỏ nhất trên đoạn 0 ; 7 2 tại điểm x 0 nào dưới đây?
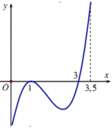
A. x 0 = 2
B. x 0 = 1
C. x 0 = 0
D. x 0 = 3
Xác định một hàm số y = f(x) thoả mãn đồng thời các điều kiện sau
f(x) xác định trên R
y = f(x) liên tục trên (−∞;0) và trên [0;+∞) nhưng gián đoạn tại x = 0
Cho hàm số f(x) có đạo hàmf'(x) xác định và liên tục trên đoạn [0;6]. Đồ thị hàm số y=f'(x) như hình vẽ bên. Biết f(0)=f(3)=f(6)=-1,f(1)=f(5)=1. Số điểm cực trị của hàm số y = [ f ( x ) ] 2 trên đoạn [0;6] là
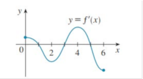
A. 5.
B. 7.
C. 9.
D. 8.
Cho các mệnh đề :
1) Hàm số y=f(x) có đạo hàm tại điểm x 0 thì nó liến tục tại x 0 .
2) Hàm số y=f(x) liên tục tại x 0 thì nó có đạo hàm tại điểm x 0 .
3) Hàm số y=f(x) liên tục trên đoạn [a;b] và f(a).f(b)<0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).
4) Hàm số y=f(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Số mệnh đề đúng là:
A. 2
B. 4
C. 3
D. 1
Cho hàm số y=f(x) xác định và liên tục trên R. Biết đồ thị của hàm số f'(x) như hình vẽ. Các điểm cực đại của hàm số y=f(x)trên đoạn [0;3] là
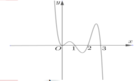
A. x=0 và x=2.
B. x=1 và x=3.
C. x=2.
D. x=0.
Cho hàm số y = f(x) xác định, liên tục trên đoạn [-2;3] và có đồ thị là đường cong trong hình vẽ bên. Tìm số điểm cực đại của hàm số y = f(x) trên đoạn [-2; 3]
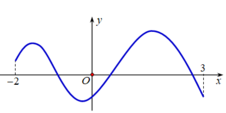
A. 1
B. 0
C. 2.
D. 3
Đáp án C.
Quan sát đồ thị hàm số, ta thấy có hai điểm cực đại thuộc đoạn [-2; 3]
Cho hàm số y = f ( x ) xác định và liên tục trên đoạn [ - 1 ; 2 ] , có đồ thị của hàm số y = f ( x ) như hình sau:
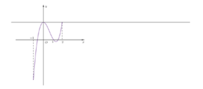
Gọi M là giá trị lớn nhất của hàm y = f ( x ) trên đoạn [ - 1 ; 2 ] . Mệnh đề nào dưới đây đúng?
A. M = f ( 1 2 )
B. M = m a x { f ( - 1 ) ; f ( 1 ) ; f ( 2 ) }
C. M = f ( 3 2 )
D. M = f ( 0 )
Đáp án là B.
Từ đồ thị của hàm số y , = f ( x ) ta có bảng biến thiên của hàm số y = f ( x ) như hình vẽ:

Từ bảng biến thiên ta có: M = m a x { f ( - 1 ) ; f ( 1 ) ; f ( 2 ) }
Cho hàm số y = f(x) xác định và liên tục trên R \ 0 biết x . f x ≠ - 1 ∀ x ≠ 0 f(1) = -2 và với ∀ x ∈ R \ 0 Tính ∫ 1 e f x d x
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y=f(x) xác định và liên tục trên [0;2] thỏa mãn e x f 2 ( x ) + f ( x ) = f ' ( x ) - 1 e x và f(0)=1. Tính f(2).
A. 1 e 2
B. - 5 3 e 2
C. - 1 e 2
D. - 2 3 e 2
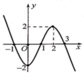
Cho hàm số y = f ( x ) xác định và liên tục trên R. Đồ thị của hàm số f(x) như hình bên. Số nghiệm thực âm của phương trình f ( f ( x ) ) = 0 bằng?
A. m = 2
B. m = 3
C. m = 7
D. m = 5