Tìm số giá trị nguyên của tham số m thuộc khoảng - 2 ; 2018 để hàm số
y = 1 3 m x 3 - m - 1 x 2 + 3 m - 2 x + 1 3
đồng biến trên nửa khoảng [ 2 ; + ∞ ) .
A. 2018
B. 2017
C. 2019
D. 2016
Tìm số giá trị nguyên của tham số m thuộc khoảng (-2;2018) để hàm số y = 1 3 m x 3 − m − 1 x 2 + 3 m − 2 x + 1 3 đồng biến trên nửa khoảng 2 ; + ∞
A. 2018
B. 2017
C. 2019
D. 2016
Cho hàm số y = m . sin x + 1 cos x + 2 . Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng - 10 ; 10 để giá trị nhỏ nhất của y nhỏ hơn -1.
A. 14
B. 13
C. 12
D. 15
số giá trị nguyên của tham số m thuộc khoảng (-10;10) để bất phương trình x (x-2)-m|x-1| +2>0 nghiệm đúng với mọi x thuộc R
Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng - 1000 ; 1000 để hàm số y = 2 x 3 - 3 2 m + 1 x 2 + 6 m m + 1 x + 1 đồng biến trên khoảng 2 ; + ∞ ?
A. 999
B. 1001
C. 1998
D. 998
Ta có:
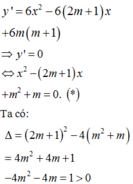
⇒ * luôn có hai nghiệm phân biệt x 1 ; x 2 x 1 < x 2 với mọi m.
Áp dụng hệ thức Vi-ét ta có:
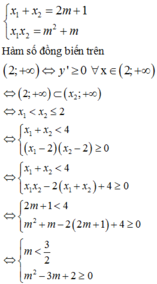
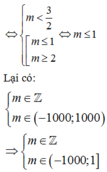
Vậy có tất cả 1001 giá trị m thỏa mãn bài toán.
Chọn B.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2018] để hàm số y = 1 3 x 3 - m x 2 + ( m + 2 ) x có hai điểm cực trị nằm trong khoảng 0 ; + ∞ .
A. 2015
B. 2016
C. 2018
D. 4035
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2018] để hàm số y = 1 3 x 3 - m x 2 + ( m + 2 ) x có hai điểm cực trị nằm trong khoảng 0 ; + ∞ .
A. 2015
B. 2016
C. 2018
D. 4035
Chọn B
Phương pháp:
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Ta sử dụng phương trình ![]() có hai nghiệm dương phân biệt
có hai nghiệm dương phân biệt
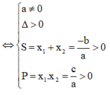
Cách giải:
Ta có ![]()
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Khi đó
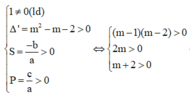
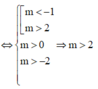
Mà ![]()
![]() nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.
nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.
Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng (-10000;10000) để hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2 + 6 m ( m + 1 ) x + 1 đồng biến trên khoảng ( 2 ; + ∞ ) ?
A. 999.
B. 1001.
C. 1998.
D. 1000.
Chọn B
Phương pháp:
Tính y'.
Tìm m để ![]()
Cách giải:
Ta có ![]()
![]()
Xét phương trình y' = 0 ![]() có
có ![]()
Suy ra phương trình y' = 0 luôn có hai nghiệm ![]()
Dễ thấy ![]() trong khoảng
trong khoảng ![]() thì hàm số đồng biến.
thì hàm số đồng biến.
Bài toán thỏa ![]()
Do ![]()
![]()
Vậy có ![]() giá trị của m thỏa mãn bài toán.
giá trị của m thỏa mãn bài toán.
Chú ý:
Cách khác: Tìm m để ![]()
Theo định lí Viet, ta có 
Hàm số đồng biến trên
(
2
;
+
∞
)
⇔
phương trình y' = 0 có hai nghiệm ![]()
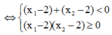
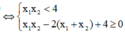

![]()
![]()
Vậy có 1001 số nguyên m thuộc khoảng (-10000;10000)
Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng (-1000;1000) để hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2 + 6 m ( m + 1 ) x + 1 đồng biến trên khoảng ( 2 ; + ∞ ) ?
A. 999.
B. 1001.
C. 1998
D. 1000.
1.Cho phương trình x2 +4x-m=0(1).Tìm tất cả các giá trị của tham số m để phương trinh (1) có đúng 1 nghiệm thuộc khoảng (-3,1)
2.Có bao nhiêu giá trị m nguyên trong nửa khoảng (0;2019] để phương trình |x2 -4|x|-5|-m có hai nghiệm phân biệt
Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 