Trong không gian Oxyz, cho ba điểm A(8;0;0), B(0;2;0), C(0;0; - 4). Phương trình mặt phẳng (ABC) là:
A. x + y - 2z = 0
B. x 4 + y 1 + z - 2 = 1
C. x 8 + y 2 + z - 4 = 0
D. x + 4y - 2z - 8 = 0
Trong không gian Oxyz, cho ba điểm A(-6;0;0), B(0;-4;0), C(0;0;6). Tập hợp tất cả các điểm M trong không gian cách đều ba điểm A, B, C là một đường thẳng có phương trình là
![]()
![]()

![]()
Chọn đáp án C.
Gọi M(x;y;z) ta có
hệ điều kiện
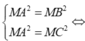
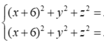
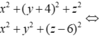
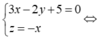
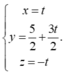
Trong không gian Oxyz, cho bốn điểm A(-1;2;0), B(3;1;0), C(0;2;1), D(1;2;2). Trong đó có ba điểm thẳng hàng là
A. A, C, D
B. A, B, D
C. B, C, D
D. A, B, C
Trong không gian Oxyz cho điểm A (3;4;3). Tổng khoảng cách từ A đến ba trục tọa độ bằng
A. 34
B. 10
C. 34 2
D. 10 + 3 2
Trong không gian Oxyz, cho điểm A ( 3 ; 4 ; 3 ) . Tổng khoảng cách từ A đến ba trục tọa độ bằng
![]()
![]()
![]()
![]()
Trong không gian Oxyz cho điểm A(3;4;3). Tổng khoảng cách từ A đến ba trục tọa độ bằng
![]()
![]()
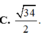
![]()
Trong không gian Oxyz cho điểm A(3;-4;3) . Tổng khoảng cách từ A đến ba trục tọa độ bằng
A. 34
B. 10
C. 34 2
D. 10 + 3 2
Trong không gian Oxyz, cho ba điểm A ( 2 ; 5 ; 3 ) , B ( 3 ; 7 ; 4 ) , C ( x ; y ; 6 ) . Giá trị của x, y để ba điểm A, B, C thẳng hàng là
A. x = 5; y = 11.
B. x = -5; y = 11.
C. x = -11; y = -5.
D. x = 11; y = 5
Trong không gian Oxyz, cho ba điểm A ( 2 ; 5 ; 3 ) ; B ( 3 ; 7 ; 4 ) ; C ( x , y , 6 ) . Giá trị của x, y để ba điểm A; B; C thẳng hàng là
A. x = 5;y = 11.
B. x = -5;y = 11.
C. x = -11;y = -5.
D. x = 11;y = 5
Chọn A.
![]()
Để 3 điểm A, B, C thẳng hàng khi và chi khi A B → , A C → cùng phương
![]()
Trong không gian Oxyz, cho ba điểm A ( 2 ; 5 ; 3 ) , B ( 3 ; 7 ; 4 ) , C ( x ; y ; 6 ) . Giá trị của x, y để ba điểm A, B, C thẳng hàng là
A. x = 5; y = 11.
B. x = -5; y = 11.
C. x = -11; y = -5.
D. x = 11; y = 5
Trong không gian Oxyz cho ba điểm A(2;1;4), B(5;0;0), C(1;-3;1). Có bao nhiêu mặt cầu qua A,B,C đồng thời tiếp xúc với mặt phẳng (Oxyz)?
A. 1
B. 0
C. 2
D. Vô số
Gọi I(a,b,c) là tâm mặt cầu ta có
![]()
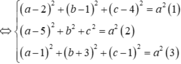
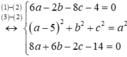
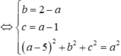
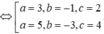
Vậy có tất cả 2 mặt cầu thoả mãn.
Chọn đáp án C.