Tìm m để (d) cắt (P) tại 2 điểm có hoành độ x1 x2 thỏa mãn x12 = x2 - 4
biết (d) : y = 2mx - 2m +1 ; (P) : y = x2
VU
Những câu hỏi liên quan
Cho (P) : y = x2 và đường thẳng (d) : y = 2mx - m + 1 với m là tham số
a) Tìm m để (P) tiếp xúc (d) tại 1 điểm
b) Gọi x1,x2 lần lượt là hoành độ giao điểm của (P) và (d). Tìm m thỏa mãn x12 x2 + mx2 = x2
a, Hoành độ giao điểm của d và P là:
x2 = 2mx -m +1 <=> x2 -2mx +m-1
đenta = 4m2-4.(m-1) = 4m2-4m+4 = (2m)2-2.2m +1 +3=(2m-1)2+3
=> đenta >= 3
Vậy không có giá trị m để P tiếp xúc với d
b,Áp dụng định lí Vi-ét:
\(\left\{{}\begin{matrix}x1+x2=2m\\x1.x2=m-1\end{matrix}\right.\)
Ta có: x12.x2 + mx2=x2
<=> x12.x2+mx2-x2=0 <=> x12.x2 + x2(m-1)=0
<=> x12.x2+x2(x1.x2)=0 <=>x12.x2+x22.x1=0
<=>x1.x2.(x1+x2)=0 <=> (m-1).2m=0
<=> \(\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)
Vậy m \(\in\) \(\left\{1;0\right\}\)
Đúng 0
Bình luận (0)
Cho (P) :y=x^2 và (d) :y=2mx-2m+1
a)CM:(d) và (p) luôn có điểm chung .Từ đó tìm tọa độ giao điểm của (d) và (p) khi m=2
b)Tìm m để( d) cắt( p) tại 2 điểm phân biệt có hoành độ x1,x2 thỏa mãn (x1)^2=x2-4
cho(P):y=x^2 và (d): y=4x-2m+1 .tìm m để (d) và (P)cắt nhau tại 2 điểm phân biệt có các hoành độ giao điểm là x1;x2 thỏa mãn|x1|+|x2|+4x1x2 lớn hơn hoăc bằng 10
cho(P):y=x^2 và (d): y=4x-2m+1 .tìm m để (d) và (P)cắt nhau tại 2 điểm phân biệt có các hoành độ giao điểm là x1;x2 thỏa mãn|x1|+|x2|+4x1x2 lớn hơn hoăc bằng 10
cho(P):y=x^2 và (d): y=4x-2m+1 .tìm m để (d) và (P)cắt nhau tại 2 điểm phân biệt có các hoành độ giao điểm là x1;x2 thỏa mãn|x1|+|x2|+4x1x2 lớn hơn hoăc bằng 10
Cho hai hàm số : (P) y = \(x^2\) và (d) y = 2mx + 2m +1 với m là tham số
Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ x1,x2 sao cho
\(\sqrt{x1+x2}\) + \(\sqrt{3+x1.x2}\) = 2m + 1
Lời giải:
PT hoành độ giao điểm:
$x^2-2mx-(2m+1)=0(*)$
Để (P) và (d) cắt nhau tại 2 điểm pb có hoành độ $x_1,x_2$ thì PT $(*)$ phải có 2 nghiệm pb $x_1,x_2$
$\Leftrightarrow \Delta'=m^2+2m+1>0\Leftrightarrow (m+1)^2>0$
$\Leftrightarrow m\neq -1$
Áp dụng định lý Viet: $x_1+x_2=2m; x_1x_2=-(2m+1)$
Khi đó:
$\sqrt{x_1+x_2}+\sqrt{3+x_1x_2}=2m+1$
$\Leftrightarrow \sqrt{2m}+\sqrt{3-2m-1}=2m+1$
\(\Leftrightarrow \left\{\begin{matrix}
0\leq m< 1\\
\sqrt{2m}+\sqrt{2(1-m)}=2m+1\end{matrix}\right.\)
Bình phương 2 vế dễ dàng giải ra $m=\frac{1}{2}$ (thỏa)
Đúng 2
Bình luận (0)
Cho hàm số
y
x
3
+
2
m
+
2
x
2
+
8
−
5
m
x
+
m
−
5
có đồ thị
C
m
và đường thẳng
d
:
y...
Đọc tiếp
Cho hàm số y = x 3 + 2 m + 2 x 2 + 8 − 5 m x + m − 5 có đồ thị C m và đường thẳng d : y = x − m + 1 . Tìm số các giá trị của m để d cắt C m tại 3 điểm phân biệt có hoành độ tại x 1 , x 2 , x 3 thỏa mãn x 1 2 + x 2 2 + x 3 2 = 20.
A. 2
B. 1
C. 3
D. 0
Đáp án A
Phương trình hoành độ giao điểm
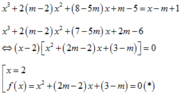
Để phương trình có 3 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt khác 2
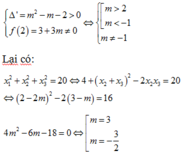
Vậy có 2 giá trị của m thỏa mãn.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ oxy, đường thẳng (d) y=2x-m+3 và Parabol (P) y=x2.
a) Tìm m để đường thẳng (d) đi qua A(1;0)
b) Tìm m để dường thẳng (d) và Parabol (P) cắt nhau tại hai điểm phân biệt có hoành độ lần lượt là x1, x2 thỏa mãn x12 -2x2 +x1.x2 = -12
Lời giải:
a. Để $(d)$ đi qua $A(1;0)$ thì:
$y_A=2x_A-m+3$
$\Leftrightarrow 0=2.1-m+3=5-m$
$\Leftrightarrow m=5$
b.
PT hoành độ giao điểm:
$x^2-(2x-m+3)=0$
$\Leftrightarrow x^2-2x+m-3=0(*)$
Để $(P), (d)$ cắt nhau tại 2 điểm pb thì $(*)$ phải có 2 nghiệm pb $x_1,x_2$
Điều này xảy ra khi:
$\Delta'=1-(m-3)>0\Leftrightarrow 4-m>0\Leftrightarrow m< 4$
Áp dụng định lý Viet: $x_1+x_2=2$ và $x_1x_2=m-3$
Khi đó:
$x_1^2-2x_2+x_1x_2=-12$
$\Leftrightarrow x_1^2-(x_1+x_2)x_2+x_1x_2=-12$
$\Leftrightarrow x_1^2-x_2^2=-12$
$\Leftrightarrow (x_1-x_2)(x_1+x_2)=-12$
$\Leftrightarrow x_1-x_2=-6$
$\Rightarrow x_1=-2; x_2=4$
$m-3=x_1x_2=(-2).4=-8$
$\Leftrightarrow m=-5$ (tm)
Đúng 0
Bình luận (0)
Cho phương trình d: y = (m + 1)x - m ( m là tham số) và Parabol (P): y = 1/2 x2
1) Tìm m để đường thẳng d cắt trục hoành tại điểm có hoành độ bằng 2.
2) Tìm m để đường thẳng d cắt (P) tại 2 điểm phân biệt có hoành độ x1, x2 thỏa mãn căn x1 + căn x2 = căn 2

