1.Cho 2 tam giác vuông ABC và DBC có cạnh huyền chung BC. Chứng minh ^DAC=^DBC;^ADB=^ACB(2 cách khác nhau). Xét 2 trường hợp :
a) A,D cùng phía với BC
b) A,D khác phía với BC
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
BA
Những câu hỏi liên quan
Hai tam giác vuông ABC và DBC chung cạnh huyền BC và hai đỉnh A,D cùng nằm trong nửa mặt phẳng bờ là đường thẳng AB.Biết ACB=20 đọ;DBC=35 độ.Tính các góc ABD;ACD
Cho 2 tam giác ABC và DBC chung cạnh huyền BC (A,D thuộc cùng một nửa mặt phẳng BC). Vẽ tia Ax sao cho AC là phân giác góc DAx. Vẽ tia Dy sao cho DB là phân giác góc ADy; Ax cắt Dy tại E, O là giao điểm Ac và BD
a) Chứng minh OE vuông góc BE
b) Chứng minh B,E,C thẳng hàng
Cho 2 tam giác vuông ABC và DBC chung cạnh huyền BC ( A,D cùng thuộc cùng một nửa mặt phẳng bờ BC). Vẽ tia Ax sao cho AC là tia phân giác của góc DAx, vẽ tia Dy sao cho DB là tia phân giác ADy, Ax cắt Dy tại E
a) Gọi O là giao điểm của AC và BD. Chứng minh OE vuông góc BE
b) Chứng minh: B,E,C thẳng hàng

a) AC là phân giác của ^DAx (gt) mà ^BAC = 900 (gt) nên AB là phân giác ngoài tại đỉnh A của \(\Delta\)ADE
Kết hợp với DB là phân giác trong tại đỉnh D của \(\Delta\)ADE
=> BE là phân giác của ^AEy
Mà EO là phân giác của ^AED (3 đường phân giác trong của \(\Delta\)AED đồng quy tại 1 điểm )
=> ^BEO = 900 (hai đường phân giác của hai góc kề bù)
Vậy OE \(\perp\)BE (đpcm)
b) Chứng minh tương tự câu a, ta được OE \(\perp\)EC
Từ đó suy ra \(BE\equiv CE\)
Vậy B,E,C thẳng hàng (đpcm)
Hai tam giác cân ABC và DBC nằm trong hai mặt phẳng khác nhau có chung cạnh đáy BC tạo nên tứ diện ABCD. Gọi I là trung điểm của cạnh BC.
a) Chứng minh BC ⊥ AD
b) Gọi AH là đường cao của tam giác ADI
Chứng minh rằng AH vuông góc với mặt phẳng (BCD).
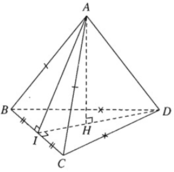
a) Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên AI ⊥ BC. Tương tự tam giác DBC cân đỉnh D và có có I là trung điểm của BC nên DI ⊥ BC. Ta suy ra:
BC ⊥ (AID) nên BC ⊥ AD.
b) Vì BC ⊥ (AID) nên BC ⊥ AH
Mặt khác AH ⊥ ID nên ta suy ra AH vuông góc với mặt phẳng (BCD).
Đúng 1
Bình luận (0)
cho tam giác ABC vuông, cân tại A. D nằm trong tam giác sao cho góc DBC =góc DCA. chứng minh tam giác DAC cân
Cho tam giác ABC và DBC vuông có chung cạnh huyền BC(A và D cùng 1 nửa mp bờ BC). vẽ tia Ax sao cho AC là pg góc DAx. vẽ tia Dy sao cho DB là pg ADy. Ax cắt Dy tại E. Gọi O là giao điểm của AC và BD. CMR: OE vuông góc với BE
Cho hai tam giác ABC và DBC có chung cạnh BC, hai đỉnh A và D nằm trong hia nửa mặt phẳng đối nhau bờ là đường thẳng BC, biết rằng cạnh BC là tic phân giác của góc ABD và góc ACD:a) So sánh các cạnh của hai tam giác ABC và DBCb) Nối A và D với một điểm E thuộc cạnh BC, so sánh AE và DE. Tìm tia phân giác của góc AEDc) Nối AD, gọi F là giao điểm của AD và BC. Chứng minh F là trung điểm của AD và AF vuông góc với BC.-
Đọc tiếp
Cho hai tam giác ABC và DBC có chung cạnh BC, hai đỉnh A và D nằm trong hia nửa mặt phẳng đối nhau bờ là đường thẳng BC, biết rằng cạnh BC là tic phân giác của góc ABD và góc ACD:
a) So sánh các cạnh của hai tam giác ABC và DBC
b) Nối A và D với một điểm E thuộc cạnh BC, so sánh AE và DE. Tìm tia phân giác của góc AED
c) Nối AD, gọi F là giao điểm của AD và BC. Chứng minh F là trung điểm của AD và AF vuông góc với BC.-
Cho hai tam giác ABC và DBC có chung cạnh BC, hai đỉnh A và D nằm trong hia nửa mặt phẳng đối nhau bờ là đường thẳng BC, biết rằng cạnh BC là tic phân giác của góc ABD và góc ACD:a) So sánh các cạnh của hai tam giác ABC và DBCb) Nối A và D với một điểm E thuộc cạnh BC, so sánh AE và DE. Tìm tia phân giác của góc AEDc) Nối AD, gọi F là giao điểm của AD và BC. Chứng minh F là trung điểm của AD và AF vuông góc với BC.
Đọc tiếp
Cho hai tam giác ABC và DBC có chung cạnh BC, hai đỉnh A và D nằm trong hia nửa mặt phẳng đối nhau bờ là đường thẳng BC, biết rằng cạnh BC là tic phân giác của góc ABD và góc ACD:
a) So sánh các cạnh của hai tam giác ABC và DBC
b) Nối A và D với một điểm E thuộc cạnh BC, so sánh AE và DE. Tìm tia phân giác của góc AED
c) Nối AD, gọi F là giao điểm của AD và BC. Chứng minh F là trung điểm của AD và AF vuông góc với BC.
Cho tam giác ABC cân tai A , đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D , gọi M là trung điểm của cạnh BC . Chứng minh rằng :
a, Tam giác DAB và taM GIÁC dac
B, TAM GIÁC DBC cân
c, A , M ,D thẳng hàng

