Cho các góc sau: \widehat{xOy}=44^o;\quad\widehat{yOz}=52^oxOy=44o;yOz=52o. Hỏi số đo góc \widehat{xOz}xOz phải có số đo bằng bao nhiêu để tia OyOy nằm giữa hai tia OxOx và OzOz?
DS
Những câu hỏi liên quan
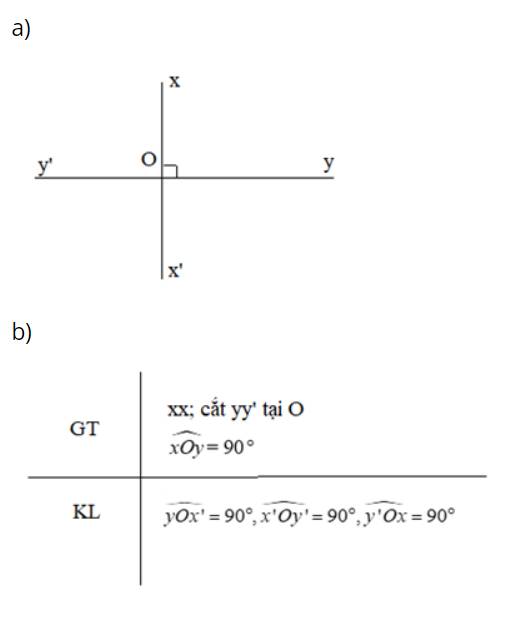
Cho định lí: “ Nếu hai đường thẳng xx’ và yy’ cắt nhau tại O và góc xOy vuông (\(\widehat {xOy}\)= 90\(^\circ \)) thì các góc\(\widehat {yOx'},\widehat {x'Oy'},\widehat {y'Ox}\) đều là góc vuông
a) Hãy vẽ hình thể hiện định lí trên
b) Viết giả thiết, kết luận của định lí
1.Cho 2 đường thẳng xx và yy cắt nhau tại O. Tính các góc còn lại, biết:a) Góc widehat{xOy}75^ob) widehat{xOy}-widehat{xOy}30^o2. Cho góc widehat{xOy}60^o. Vẽ tia Ox và Oy là tia đối của Ox và Oy. Tia phân giác Om của góc widehat{xOy} , vẽ tia đối Om là tia đối của tia Om.a) CMR: Om là tia phân giác của góc widehat{xOy}b) Viết tên các cặp góc đối đỉnh.
Đọc tiếp
1.Cho 2 đường thẳng xx' và yy' cắt nhau tại O. Tính các góc còn lại, biết:
a) Góc \(\widehat{xOy}=75^o\)
b) \(\widehat{x'Oy}-\widehat{xOy}=30^o\)
2. Cho góc \(\widehat{xOy}=60^o\). Vẽ tia Ox' và Oy' là tia đối của Ox và Oy. Tia phân giác Om của góc \(\widehat{xOy}\) , vẽ tia đối Om' là tia đối của tia Om.
a) CMR: Om' là tia phân giác của góc \(\widehat{x'Oy'}\)
b) Viết tên các cặp góc đối đỉnh.
Cho đường thẳng x x' và y y' tại o .Sao cho \(\widehat{xoy}\)= 90 độ .So sánh các góc \(\widehat{xoy'},\widehat{x'oy,}\widehat{x'oy'}\)
Ta có: góc xOy + góc xOy' = 180 độ ( vì 2 góc kề bù)
Mà : góc xOy = 90 độ
Suy ra xOy' = 180 độ - 90 độ = 90 độ ( 1)
Ta có: góc xOy' + góc x'Oy' = 180 độ ( vì 2 góc kề bù)
Mà : góc xOy' = 90 độ
Suy ra x'Oy' = 180 độ - 90 độ = 90 độ (2)
Ta có: góc xOy + góc x'Oy = 180 độ ( vì 2 góc kề bù)
Mà : góc xOy = 90 độ
Suy ra x'Oy = 180 độ - 90 độ = 90 độ ( 3 )
Từ ( 1) (2) (3) suy ra :
Góc xOy = góc xOy' = góc x'Oy' = góc x'Oy = 90 độ
Đúng 0
Bình luận (0)
Chọn từ "nhọn", "vuông", "tù", "bẹt" thích hợp cho ?:
a) Nếu \(\widehat{xOy}=90^o\) thì góc xOy là góc ?;
b) Nếu \(\widehat{mIn}=75^o\) thì góc mIn là góc ?;
c) Nếu \(\widehat{uHv}=136^o\) thì góc uHv là góc?;
d) Nếu \(\widehat{zKt}=180^o\) thì góc zKt là góc ?.
Xem thêm câu trả lời
1.Cho 2 đường thẳng xx và yy cắt nhau tại O. Tính các góc còn lại, biết:a) Góc widehat{xOy}75^ob) widehat{xOy}-widehat{xOy}30^o2. Cho góc widehat{xOy}60^o. Vẽ tia Ox và Oy là tia đối của Ox và Oy. Tia phân giác Om của góc widehat{xOy} , vẽ tia đối Om là tia đối của tia Om.a) CMR: Om là tia phân giác của góc widehat{xOy}b) Viết tên các cặp góc đối đỉnh.Các bn giúp mk với, mk đã hỏi câu này lần thứ 2 rồi, mk đg rất cần :)))
Đọc tiếp
1.Cho 2 đường thẳng xx' và yy' cắt nhau tại O. Tính các góc còn lại, biết:
a) Góc \(\widehat{xOy}=75^o\)
b) \(\widehat{x'Oy}-\widehat{xOy}=30^o\)
2. Cho góc \(\widehat{xOy}=60^o\). Vẽ tia Ox' và Oy' là tia đối của Ox và Oy. Tia phân giác Om của góc \(\widehat{xOy}\) , vẽ tia đối Om' là tia đối của tia Om.
a) CMR: Om' là tia phân giác của góc \(\widehat{x'Oy'}\)
b) Viết tên các cặp góc đối đỉnh.
Các bn giúp mk với, mk đã hỏi câu này lần thứ 2 rồi, mk đg rất cần :)))
1.
Giải: a) Ta có: \(\widehat{xOy}+\widehat{yOx'}=180^0\) (kề bù)
=> \(\widehat{yOx'}=180^0-\widehat{xOy}=180^0-75^0=105^0\)
Ta lại có: \(\widehat{xOy}=\widehat{x'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOy}=75^0\) => \(\widehat{x'Oy'}=75^0\)
\(\widehat{yOx'}=\widehat{xOy'}\) (đối đỉnh)
Mà \(\widehat{yOx'}=105^0\) => \(\widehat{xOy'}=105^0\)
Đúng 0
Bình luận (0)
1b) Ta có: \(\widehat{xOy}+\widehat{x'Oy}=180^0\) (kề bù)
mà \(\widehat{x'Oy}-\widehat{xOy}=30^0\)
=> \(2.\widehat{x'Oy}=210^0\)
=> \(\widehat{x'Oy}=210^0:2=105^0\) => \(\widehat{x'Oy}=\widehat{xOy'}=105^0\) (đối đỉnh)
=> \(\widehat{xOy}=180^0-105^0=75^0\) => \(\widehat{xOy}=\widehat{x'Oy'}=75^0\) (đối đỉnh)
2.
Giải: a) Ta có: \(\widehat{xOm}=\widehat{x'Om'}\) (đối đỉnh)
\(\widehat{mOy}=\widehat{m'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOm}=\widehat{mOy}\) (gt)
=> \(\widehat{x'Om'}=\widehat{m'Oy'}\)
Ta lại có: \(\widehat{xOy}=\widehat{x'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOm}=\widehat{mOy}=\frac{1}{2}.\widehat{xOy}\) (vì Om là tia p/giác)
=> \(\widehat{x'Om'}=\widehat{m'Oy'}=\frac{1}{2}.\widehat{xOy}\)
=> Om' nằm giữa Ox' và Oy'
=> Om' là tia p/giác của góc x'Oy'
b) Tự viết
Đúng 0
Bình luận (0)
Cho 2 đường thẳng xx' và yy' cắt nhau tại O biết \(\widehat{xoy}\) =40o.
a,Tính các góc \(\widehat{x'Oy'},\widehat{x'Oy},\widehat{xOy'}\)
b,Vẽ tia phân giác Om của góc xOy , tia On là tia phân giác của góc x'Oy'.Hỏi Om và On có đối nhau không? chứng minh
a) +) Vì Ox đối với Ox' và Oy đối với Oy' nên \(\widehat{xOy}\) và \(\widehat{x'Oy'}\) đối đỉnh
\(\Rightarrow\)\(\widehat{xOy}=\)\(\widehat{x'Oy'}\)
hay \(\widehat{x'Oy'}\)\(=40^0\)
+) Ta có: \(\widehat{xOy}+\widehat{x'Oy}=180^0\) (kề bù)
hay \(40^0+\widehat{x'Oy}=180^0\)
\(\Leftrightarrow\widehat{x'Oy}=180^0-40^0\)
\(\Leftrightarrow\widehat{x'Oy}=140^0\)
+) Ta có: \(\widehat{xOy}+\widehat{xOy'}=180^0\) (kề bù)
hay \(40^0+\widehat{xOy'}=180^0\)
\(\Leftrightarrow\widehat{xOy'}=180^0-40^0\)
\(\Leftrightarrow\widehat{xOy'}=140^0\)
b) Vì \(\widehat{xOy}=\widehat{x'Oy'}\)(hai góc đối đỉnh)
Mà Om là tia phân giác của góc xOy và On là tia phân giác của x'Oy' nên Om đối On (đpcm)
Đúng 0
Bình luận (0)
a, Vì góc x'Oy' và góc xOy là hai góc đối đỉnh, mà \(\widehat{xOy}=40^0\)nên \(\widehat{x'Oy'}=40^0\). Góc xOy và góc xOy' là hai góc kề bù nên \(\widehat{xOy}+\widehat{xOy'}=180^0\)hay \(40^0+\widehat{xOy'}=180^0\)
=> \(\widehat{xOy'}=180^0-40^0=140^0\)
Góc xOy' là góc đối đỉnh với góc xOy' nên \(\widehat{xOy}=\widehat{x'Oy}=140^0\)
b, Om,On theo thứ tự là các tia phân giác của hai góc xOy và x'Oy' nên \(\widehat{xOm}=\widehat{mOy}=\frac{1}{2}\widehat{xOy}\)và \(\widehat{nOx'}=\widehat{mOy'}=\frac{1}{2}\widehat{x'Oy'}\)mà \(\widehat{xOy}=\widehat{x'Oy'}\), do đó \(\widehat{xOm}=\widehat{mOy}=\widehat{nOx'}=\widehat{nOy'}=\frac{1}{2}\widehat{xOy}\).
Ta có : \(\widehat{xOm}=\widehat{nOy'}=\widehat{y'Ox}=\widehat{xOm}=\widehat{y'Ox}+\widehat{xOm}+\widehat{mOy}\)
\(=\widehat{y'Ox}+\widehat{xOy}=180^0\)
Góc mOn là góc bẹt,vì thế hai tia Om,On là hai tia đối nhau
Đúng 0
Bình luận (0)
Biết \widehat{xOy}=44^oxOy=44o có tia phân giác là tia OtOt.
Tính số đo góc xOtxOt.
ghi lại đề : \(\widehat{xOy}=44^o\)OT-pg \(\widehat{xOy}\)
tính \(\widehat{xOt}\)
ta có : OT-pg \(\widehat{xOy}\)
=>\(\widehat{xOt}=\widehat{yOt}=\frac{\widehat{xOy}}{2}=\frac{40^o}{2}=20^o\)
Vậy \(\widehat{xOt}=20^o\)
chết rồi mình làm giữa chừng lại sai rồi ; bạn thay 40o thành 44o và đáp số là 22o nhé!
Cho 2 góc kề nhau \(\widehat{xOy}\)và \(\widehat{yOz}\). Gọi OA là tia phân giác của góc \(\widehat{xOy}\), OB là tia phân giác của \(\widehat{zOy}\). Tính số đo góc \(\widehat{AOB}\)biết góc \(\widehat{xOy}+\widehat{yOz}=150^o\)
P/S : Đề không sai nha các bạn
AOB=AOy+BOy
=yOz/2+xOy/2
=yOz+xOy/2=150/2=75
Đúng 0
Bình luận (0)
Ta có: \(\widehat{xOy}+\widehat{yOz}=150^o\)
Vì OA là phân giác \(\widehat{xOy}\)nên suy ra \(\widehat{xOA}=\widehat{AOy}=\frac{1}{2}\widehat{xOy}\)
Vì OB là tia phân giác \(\widehat{zOy}\)nên suy ra \(\widehat{yOB}=\widehat{BOy}=\frac{1}{2}\widehat{yOz}\)
Vậy suy ra: \(\widehat{AOB}=\widehat{AOy}+\widehat{yOB}=\frac{1}{2}\widehat{xOy}+\frac{1}{2}\widehat{yOz}=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\frac{1}{2}.150^o=75^o\)
Đúng 0
Bình luận (0)
Cho 2 đường thẳng x'x và y'y cắt nhau tại O.
1. Cho biết \(\widehat{xOy}\) = 42o . Tính các góc còn lại
2. Cho biết \(\widehat{xOy}\) = 90o . Tính các góc còn lại
Nêu một nhận xét trong trường hợp này
CÓ GÓC XOY VÀ GÓC X'OY LÀ 2 GÓC KỀ BÙ
SUY RA GÓC XOY+ GÓC X'OY= 180 ĐỘ
THAY SỐ XOY = 42 ĐO ĐƯỢC
42 ĐỘ + X'OY= 180 ĐỘ
X'OY = 180 ĐỘ -42 ĐỘ
X'OY = 138 ĐỘ
CÁC CẦU KHÁC TÍNH NHƯ THẾ NHA
K CHO MINH NHE
Đúng 0
Bình luận (0)