Vẽ đồ thị hàm số \(y = \cos x\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) rồi xác định số nghiệm của phương trình 3cosx + 2 = 0 trên đoạn đó.
QL
Những câu hỏi liên quan
Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:
a) \(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\)
b) \(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\)
a) Vẽ đồ thị:
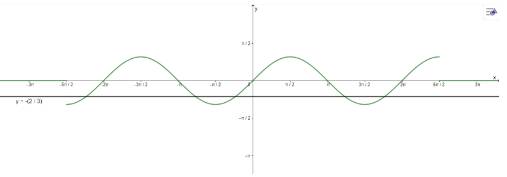
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:
\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm
Đúng 0
Bình luận (0)
Đồ thị của các hàm số \(y = \sin x\) và \(y = \cos x\) cắt nhau tại bao nhiêu điểm có hoành độ thuộc đoạn \(\left[ { - 2\pi ;\frac{{5\pi }}{2}} \right]\)?
A. 5 B. 6 C. 4 D. 7
Phương trình hoàn độ giao điểm của hai đồ thì hàm số là \(\sin x = \cos x\)
\( \Leftrightarrow \tan x = 1 \Leftrightarrow x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
Do \(x \in \left[ { - 2\pi ;\frac{{5\pi }}{2}} \right]\; \Leftrightarrow - 2\pi \le \frac{\pi }{4} + k\pi \le \frac{{5\pi }}{2}\;\; \Leftrightarrow \; - \frac{9}{4} \le k \le \frac{9}{4}\;\;\;\)
Mà \(k\; \in \mathbb{Z}\;\; \Leftrightarrow k\; \in \left\{ { - 2;\; - 1;0;1;2} \right\}\)
Vậy ta chọn đáp án A
Đúng 0
Bình luận (0)
BT
2 tháng 9 2016 lúc 21:26
xét hàm số y f(x) cosfrac{x}{2}.a) chứng minh rằng với mỗi số nguyên k , fleft(x+k4piright)f(x) với mọi x .b) lập bảng biến thiên của hàm số y cosfrac{x}{2} trên đoạn left[-2pi;2piright].c) vẽ đồ thị các hàm số y cos x và y cosfrac{x}{2} trong cùng một hệ tọa độ vuông góc Oxy .d) trong mặt phẳng tọa độ Oxy , xét phép biến hình F biến mỗi điểm (x ; y) thành (x ; y) sao cho x2x và yy . chứng minh rằng F biến đồ thị hàm số y cos x thành đồ thị hàm số y cosfrac{x}{2} .
Đọc tiếp
xét hàm số y = f(x) = \(\cos\frac{x}{2}\).
a) chứng minh rằng với mỗi số nguyên k , f\(\left(x+k4\pi\right)\)=f(x) với mọi x .
b) lập bảng biến thiên của hàm số y = \(\cos\frac{x}{2}\) trên đoạn \(\left[-2\pi;2\pi\right]\).
c) vẽ đồ thị các hàm số y = \(\cos x\) và y = \(\cos\frac{x}{2}\) trong cùng một hệ tọa độ vuông góc Oxy .
d) trong mặt phẳng tọa độ Oxy , xét phép biến hình F biến mỗi điểm (x ; y) thành (x' ; y') sao cho x'=2x và y'=y . chứng minh rằng F biến đồ thị hàm số y = \(\cos x\) thành đồ thị hàm số y = \(\cos\frac{x}{2}\) .
Tịnh tiến đồ thị hàm số y= cos x sang phải \(\dfrac{\pi}{2}\) ta được đồ thị hàm số nào
A. \(y=sinx\)
B.\(y=-cosx\)
C.\(y=\)\(cos\left(x+\dfrac{\pi}{2}\right)\)
D.\(y=sin\left(x-\dfrac{\pi}{2}\right)\)
BT
31 tháng 8 2016 lúc 19:35
xét hàm số y f(x) cosfrac{x}{2}.a) chứng minh rằng với mỗi số nguyên k , fleft(x+k4piright)f(x) với mọi x .b) lập bảng biến thiên của hàm số y cosfrac{x}{2} trên đoạn left[-2pi;2piright].c) vẽ đồ thị các hàm số y cos x và y cosfrac{x}{2} trong cùng một hệ tọa độ vuông góc Oxy .d) trong mặt phẳng tọa độ Oxy , xét phép biến hình F biến mỗi điểm (x ; y) thành (x ; y) sao cho x2x và yy . chứng minh ằng F biến đồ thị hàm số y cos x thành đồ thị hàm số y cosfrac{x}{2}.
Đọc tiếp
xét hàm số y = f(x) = \(\cos\frac{x}{2}\).
a) chứng minh rằng với mỗi số nguyên k , f\(\left(x+k4\pi\right)\)=f(x) với mọi x .
b) lập bảng biến thiên của hàm số y = \(\cos\frac{x}{2}\) trên đoạn \(\left[-2\pi;2\pi\right]\).
c) vẽ đồ thị các hàm số y = \(\cos x\) và y = \(\cos\frac{x}{2}\) trong cùng một hệ tọa độ vuông góc Oxy .
d) trong mặt phẳng tọa độ Oxy , xét phép biến hình F biến mỗi điểm (x ; y) thành (x' ; y') sao cho x'=2x và y'=y . chứng minh ằng F biến đồ thị hàm số y = \(\cos x\) thành đồ thị hàm số y = \(\cos\frac{x}{2}\).
BT
4 tháng 9 2016 lúc 15:46
xét hàm số y f(x) cosfrac{x}{2}.a) chứng minh rằng với mỗi số nguyên k , fleft(x+k4piright)f(x) với mọi x .b) lập bảng biến thiên của hàm số y cosfrac{x}{2} trên đoạn left[-2pi;2piright].c) vẽ đồ thị các hàm số y cos x và y cosfrac{x}{2} trong cùng một hệ tọa độ vuông góc Oxy .d) trong mặt phẳng tọa độ Oxy , xét phép biến hình F biến mỗi điểm (x ; y) thành (x ; y) sao cho x2x và yy . chứng minh rằng F biến đồ thị hàm số y cos x thành đồ thị hàm số y cosfrac{x}{2} .
Đọc tiếp
xét hàm số y = f(x) = \(\cos\frac{x}{2}\).
a) chứng minh rằng với mỗi số nguyên \(k\) , f\(\left(x+k4\pi\right)\)=f(x) với mọi x .
b) lập bảng biến thiên của hàm số y =\(\cos\frac{x}{2}\) trên đoạn \(\left[-2\pi;2\pi\right]\).
c) vẽ đồ thị các hàm số y = \(\cos x\) và y = \(\cos\frac{x}{2}\) trong cùng một hệ tọa độ vuông góc Oxy .
d) trong mặt phẳng tọa độ Oxy , xét phép biến hình F biến mỗi điểm (x ; y) thành (x' ; y') sao cho x'=2x và y'=y . chứng minh rằng F biến đồ thị hàm số y = \(\cos x\) thành đồ thị hàm số y =\(\cos\frac{x}{2}\) .
BT
5 tháng 9 2016 lúc 19:36
xét hàm số y f(x) cosfrac{x}{2}.a) chứng minh rằng với mỗi số nguyên kk , fleft(x+k4piright)f(x) với mọi x .b) lập bảng biến thiên của hàm số y cosfrac{x}{2} trên đoạn left[-2pi;2piright].c) vẽ đồ thị các hàm số y cos x và y cosfrac{x}{2} trong cùng một hệ tọa độ vuông góc Oxy .d) trong mặt phẳng tọa độ Oxy , xét phép biến hình F biến mỗi điểm (x ; y) thành (x ; y) sao cho x2x và yy . chứng minh rằng F biến đồ thị hàm số y cos x thành đồ thị hàm số y cosfrac{x}{2} .
Đọc tiếp
xét hàm số y = f(x) = \(\cos\frac{x}{2}\).
a) chứng minh rằng với mỗi số nguyên kk , f\(\left(x+k4\pi\right)\)=f(x) với mọi x .
b) lập bảng biến thiên của hàm số y =\(\cos\frac{x}{2}\) trên đoạn \(\left[-2\pi;2\pi\right]\).
c) vẽ đồ thị các hàm số y = \(\cos x\) và y = \(\cos\frac{x}{2}\) trong cùng một hệ tọa độ vuông góc Oxy .
d) trong mặt phẳng tọa độ Oxy , xét phép biến hình F biến mỗi điểm (x ; y) thành (x' ; y') sao cho x'=2x và y'=y . chứng minh rằng F biến đồ thị hàm số y =\(\cos x\) thành đồ thị hàm số y =\(\cos\frac{x}{2}\) .
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\) để hàm số \(y = \cot x\) nhận giá trị dương.
Hàm số nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\), thì \(y > 0\) khi \(x\; \in \left( {0;\frac{\pi }{2}} \right) \cup \left( {\;\pi ;\frac{{3\pi }}{2}} \right)\)
Đúng 0
Bình luận (0)
BT
4 tháng 9 2016 lúc 15:37
a) từ đồ thị hàm số y = \(\cos x\) , hãy suy ra đồ thị các hàm số sau và vẽ đô thị các hàm số đó : y = \(\cos x+2\) ; y = \(\cos\left(x-\frac{\pi}{4}\right)\).
b) hỏi mỗi hàm số đó có phải là hàm số tuần hoàn không ?