a) Ta có:

\(\frac{4}{15}+\frac{1}{6}-\frac{4}{9}>\frac{2}{3}-x-\frac{1}{4}\\ \Rightarrow x+\frac{4}{15}+\frac{1}{6}-\frac{4}{9}>\frac{2}{3}-\frac{1}{4}\\ \Rightarrow x>\frac{2}{3}+\frac{4}{9}-\frac{1}{4}-\frac{1}{6}-\frac{4}{15}\\ \Rightarrow x>\left(\frac{6}{9}+\frac{4}{9}\right)-\left(\frac{15}{60}+\frac{10}{60}+\frac{16}{60}\right)\)

\(x>\frac{10}{9}-\frac{41}{60}\\ x>\frac{200-123}{180}\Rightarrow x>\frac{77}{180}\)

b) Bất đẳng thức kép

\(4-1\frac{1}{3}< x+\frac{1}{5}< 12\frac{2}{7}-3\frac{3}{8}\)

có nghĩa là ta phải có hai bất đẳng thức đồng thời:

\(x+\frac{1}{5}>4-1\frac{1}{3}\) và \(x+\frac{1}{5}< 12\frac{2}{7}-3\frac{3}{8}\)

Ta tìm các giá trị của x cần thỏa mãn bất đẳng thức thứ nhất:

\(x+\frac{1}{5}>4-1\frac{1}{3}\Rightarrow x>4-1\frac{1}{3}-\frac{1}{5}\\ \Rightarrow x>\frac{37}{15}\)

Từ bất đẳng thức thứ hai

\(x+\frac{1}{5}< 12\frac{2}{7}-3\frac{3}{8}\Rightarrow x< \frac{86}{7}-\frac{27}{8}-\frac{1}{5}\\ \Rightarrow x< \frac{2439}{280}.\)

Như vậy các số hữu tỉ x cần thỏa mãn:

\(\frac{37}{15}< x< \frac{2439}{280}\)

b) 4 chứ không phải b.4 nhé

Lát đăng tiếp, giờ mắc học pài với ăn cơm, ngày mai kiểm tar sử nữa

 Với y = 0

 \(\Rightarrow3^x-4^y=242\)    \(\Rightarrow3^x-4^0=242\)        \(\Rightarrow3^x=243\)

\(\Rightarrow3^x=3^5\)  \(\Rightarrow x=5\)

\(\Rightarrow3^x=242+4^y\)

Với y > 0

\(\Rightarrow242+4^y\) là số chẵn mà \(3^y\) là số lẻ

\(\Rightarrow3^x-4^y=242\) không có giá trị x,y thỏa mãn

Vậy y = 0 ; x = 5 là giá trị cần tìm

\(x=5;y=0\)

Tham khảo nha !!! 

Trình bày đầy đủ hộ mình với >_<

Trả lời:

Vì A = 16 x 2 – 24 + 9 = ( 4 x   –   3 ) 2  nên:

a) x= 0 thì A = 9;                        b) x = 1 4  thì A = 4;

c) x = 12 thì A = 2025;               d) x = 3 4 thì A = 0.

1a) \(0,31:0,91=x:\frac{49}{3}\)

=> \(\frac{0,31}{0,91}=\frac{3x}{49}\)

=> \(3x=\frac{3}{7}.49\)

=> \(3x=21\)

=> \(x=21:3=7\)

b) \(6,88:x=12:27\)

=> \(\frac{6,88}{x}=\frac{12}{27}\)

=> \(x=6,88:\frac{4}{9}\)

=> \(x=15,48\)

c) \(\frac{25}{3}:\frac{35}{3}=13:2x\)

=> \(\frac{13}{2x}=\frac{5}{7}\)

=> \(2x=13:\frac{5}{7}\)

=> \(2x=\frac{91}{5}\)

=> \(x=\frac{91}{5}:2=\frac{91}{10}\)

d) \(\left(x-1\right):24,5=5:8,75\)

=> \(\frac{x-1}{24,5}=\frac{5}{8,75}\)

=> \(x-1=\frac{4}{7}.24,5\)

=> \(x-1=14\)

=> \(x=14+1=15\)

2a) Ta có: \(\frac{x}{y}=\frac{5}{7}\) => \(\frac{x}{5}=\frac{y}{7}\)

Áp dụng t/c của dãy tỉ số bằng nhau, ta có:

   \(\frac{x}{5}=\frac{y}{7}=\frac{x+y}{5+7}=\frac{4,08}{12}=0,34\)

=> \(\hept{\begin{cases}\frac{x}{5}=0,34\\\frac{y}{7}=0,34\end{cases}}\) => \(\hept{\begin{cases}x=0,34.5=1,7\\y=0,34.7=2,38\end{cases}}\)

Vậy x = 1,7; y = 2,38

b) Ta có: \(\frac{x}{y}=-\frac{3}{7}\) => \(\frac{x}{-3}=\frac{y}{7}\)

Áp dụng t/c của dãy tỉ số bằng nhau, ta có:

  \(\frac{x}{-3}=\frac{y}{7}=\frac{x-y}{-3-7}=\frac{-40}{-10}=4\)

=> \(\hept{\begin{cases}\frac{x}{-3}=4\\\frac{y}{7}=4\end{cases}}\) => \(\hept{\begin{cases}x=4.\left(-3\right)=-12\\y=4.7=28\end{cases}}\)

vậy x = -12; y = 28

c) Ta có: \(\frac{x}{y}=\frac{3}{5}\) => \(\frac{x}{3}=\frac{y}{5}\)

Đặt : \(\frac{x}{3}=\frac{y}{5}=k\) => \(\hept{\begin{cases}x=3k\\y=5k\end{cases}}\) (*)

Khi đó, ta có: xy = 1215

hay 3k. 5k = 1215

=> 15k² = 1215

=> k² = 1215 : 15 = 81

=> k = \(\pm\)9 

Thay k = \(\pm\)9 vào (*), ta được:

+) x = 3. (\(\pm\)9) = \(\pm\)27

+) y = 5. (\(\pm\)9) = \(\pm\)45

Vậy ...

Mơn bn nhiều <3

Điều hòa tim mạch bằng phản xạ sinh dưỡng trong các trường hợp :

    - Lúc huyết áp tăng cao

    Thụ quan áp lực bị kích thích , xuất hiện xung thần kinh dẫn truyền về trung ương phụ trách tim mạch nằm trong các nhân xám thuộc bộ phận đối giao cảm, theo dây li tâm (dây X hay mê tẩu) tới tim làm giảm nhịp tim và lực co đồng thời làm dãn các mạch da và mạch ruột gây hạ huyết áp (có thể tham khảo hình 48 – 2 trong bài).

    - Hoạt động lao động

    Khi lao động xảy ra sự ôxi hóa glucôzơ để tạo năng lượng cần cho sự co cơ, đồng thời sản phẩm phân hủy của quá trình này là CO2 tích lũy dần trong máu. (Đúng ra là H+ được hình thành do :

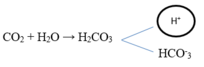
    H+ sẽ kích thích thụ quan gây ra xung thần kinh hướng tâm truyền về trung khu hô hấp và tuần hoàn nằm trong hành tủy, truyền tới trung khu giao cảm, theo dây giao cảm đến tim, mạch máu đến cơ làm tăng nhịp tim, lực co tim và mạch máu co giãn để cung cấp O2 cần cho nhu cầu năng lượng co cơ, đồng thời chuyển nhanh sản phẩm phân hủy đến các cơ quan bài tiết).