Cho tứ giác ABCD thay đổi, luôn nội tiếp đường tròn (O;\(\sqrt{5}\)cm) và có hai đường chéo vuông góc với nhau tại I sao cho IO=1cm. Diện tích tam giác ICD đạt GTLN là ... \(cm^2\) .
TT
Những câu hỏi liên quan
1.cho tứ giác abcd thay đổi luôn nội tiếp đường tròn (O; căn 5) có hai đường chéo vuông góc với nhau tại I sao cho IO=1cm.Diện tích tam giac ICD dat GTLN.............(cm2)
Nhận xét : A, B, C, D có vai trò bình đẳng nhau nên nếu O không thuộc miền trong ∆ICD, chẳng hạn O thuộc miền trong ∆IAD, khi đó dễ dàng thấy S(ICD) < S(IAD). Vậy chỉ xét trường hợp O thuộc miền trong ∆ICD.
Vẽ OH _|_ AC tại H; Vẽ OK _|_ BK tại K => IK = OH; IH = OK. Đặt IC = a > 0; ID = b > 0;
Ta có: CH = IC - IH <=> CH² = IC² + IH² - 2IC.IH <=> OC² - OH² = IC² + OK² - 2IC.OK <=> 2IC.OK = IC² - OC² + (OH² + OK²) = IC² - OC² + OI² <=> 2a.OK = a² - 5 + 1 = a² - 4 <=> 2OK = a - 4/a <=> 4OK² = a² + 16/a² - 8 (1)
Tương tự : 4OH² = b² + 16/b² - 8 (2)
(1) + (2) : a² + b² + 16(1/a² + 1/b²) - 16 = 4(OH² + OK²) = 4OI² = 4
<=> a² + b² + 16(1/a² + 1/b²) = 20
<=> ab + 16/ab ≤ 10 (vì 2ab ≤ a² + b² ; 2/ab ≤ 1/a² + 1/b²)
<=> S² - 5S + 4 ≤ 0 ( với S = ab/2 = S(ICD))
<=> (S - 5/2)² ≤ 9/4
<=> - 3/2 ≤ S - 5/2 ≤ 3/2
<=> 1 ≤ S ≤ 4
Vậy Max S = 4 khi a = b = 2√2; Min S = 1 khi a = b = √2
Đúng 0
Bình luận (0)
Nhận xét : A, B, C, D có vai trò bình đẳng nhau nên nếu O không thuộc miền trong ∆ICD, chẳng hạn O thuộc miền trong ∆IAD, khi đó dễ dàng thấy S(ICD) < S(IAD). Vậy chỉ xét trường hợp O thuộc miền trong ∆ICD. <br>Vẽ OH _|_ AC tại H; Vẽ OK _|_ BK tại K => IK = OH; IH = OK. Đặt IC = a > 0; ID = b > 0; <br>Ta có: CH = IC - IH <=> CH² = IC² + IH² - 2IC.IH <=> OC² - OH² = IC² + OK² - 2IC.OK <=> 2IC.OK = IC² - OC² + (OH² + OK²) = IC² - OC² + OI² <=> 2a.OK = a² - 5 + 1 = a² - 4 <=> 2OK = a - 4/a <=> 4OK² = a² + 16/a² - 8 (1) <br>Tương tự : 4OH² = b² + 16/b² - 8 (2) <br>(1) + (2) : a² + b² + 16(1/a² + 1/b²) - 16 = 4(OH² + OK²) = 4OI² = 4 <br><=> a² + b² + 16(1/a² + 1/b²) = 20 <br><=> ab + 16/ab ≤ 10 (vì 2ab ≤ a² + b² ; 2/ab ≤ 1/a² + 1/b²) <br><=> S² - 5S + 4 ≤ 0 ( với S = ab/2 = S(ICD)) <br><=> (S - 5/2)² ≤ 9/4 <br><=> - 3/2 ≤ S - 5/2 ≤ 3/2 <br><=> 1 ≤ S ≤ 4 <br>Vậy Max S = 4 khi a = b = 2√2; Min S = 1 khi a = b = √2
Đúng 0
Bình luận (0)
Cho tứ giác ABCD thay đổi, luôn nội tiếp đường tròn tâm O bán kính căn 5 cm và có 2 đường chéo vuông góc với nhau tại I sao cho OI=1cm . Diện tích tam giác IDC lớn nhất là .. cm^2
Cho tứ giác ABCD thay đổi, luôn nội tiếp đường tròn (O;\(\sqrt{5} \)) và có 2 đường chéo vuông góc với nhau tại I sao cho IO=1.
Diện tích lớn nhất của tam giác ICD là
Đáp án là 4 bạn ak
còn về cách giải thì khá là phức tạp
Đúng 0
Bình luận (0)
trên mạng có bài giống thế này đấy
MaxS=4; Mín=1
Đúng 0
Bình luận (0)
Cho tứ giác ABCD thay đổi , luôn nội tiếp đường tròn \(\left(O;\sqrt{5}\right)\) và có hai đường chép vuông góc với nhau tại I sao cho OI=1 cm.Tìm GTLN của tam giác ICD.
ID=IC=\(\sqrt{3}+2\sqrt{2}\)
S max = \(\frac{11+4\sqrt{6}}{2}\)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD thay đổi, luôn nội tiếp đường tròn \(\left(O;\sqrt{5}cm\right)\) và có hai đường chéo vuông góc với nhau tại I sao cho IO = 1cm.
Diện tích tam giác ICD đạt giá trị lớn nhất là bn?
Cho tam giác đều ABC nội tiếp đường tròn tâm O. 1 đường thẳng d thay đổi nhưng luôn đi qua A cắt 2 tiếp tuyến tại B và C của đường tròn tương ứng tại M và N. Giả sử đường thẳng d cắt lại đường tròn tâm O tai E (E khác A). MC cắt BN tại F Chứng minh a) tam giác ACN đồng dạng tam giác MBA tam giác MBC đồng dạng tam giác BCN b) Tứ giác BMEF nội tiếp c) Đường thẳng EF luôn luôn đi qua 1 điểm cố định khi d thay đổi nhưng đi qua A
Đọc tiếp
Cho tam giác đều ABC nội tiếp đường tròn tâm O. 1 đường thẳng d thay đổi nhưng luôn đi qua A cắt 2 tiếp tuyến tại B và C của đường tròn tương ứng tại M và N. Giả sử đường thẳng d cắt lại đường tròn tâm O tai E (E khác A). MC cắt BN tại F
Chứng minh
a) tam giác ACN đồng dạng tam giác MBA
tam giác MBC đồng dạng tam giác BCN
b) Tứ giác BMEF nội tiếp
c) Đường thẳng EF luôn luôn đi qua 1 điểm cố định khi d thay đổi nhưng đi qua A
Cho hình thang ABCD có AB // CD và AB 2a, BC CD DA a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.b) Gọi O là trung điểm của AB, O là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO ⊥ (SBC).c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.d) Tìm một điểm cách đ...
Đọc tiếp
Cho hình thang ABCD có AB // CD và AB = 2a, BC = CD = DA = a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.
a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.
b) Gọi O là trung điểm của AB, O' là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO' ⊥ (SBC).
c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.
d) Tìm một điểm cách đều các điểm A, B, C, D, I, J, K và tìm khoảng cách đó.
e) Gọi M là giao điểm của JK và (ABCD). Chứng minh rằng AM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
f) Khi S thay đổi trên d, các điểm I, J, K lần lượt chạy trên đường nào.
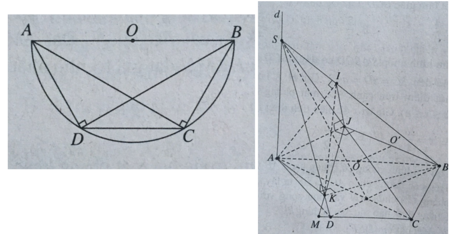
Nhận xét
Hình thang ABCD có hai cạnh bên và đáy nhỏ bằng nhau và bằng nửa đáy lớn, nên nó là nửa lục giác đều nội tiếp trong đường tròn đường kính AB, tâm O là trung điểm của AB.
Như vậy: ∠(ACB) = ∠(ADB) = 1v.
a) Theo giả thiết, ta có: SA ⊥ (ABCD) ⇒ SA ⊥ BC
BC ⊥ SA & BC ⊥ AC ⇒ BC ⊥ (SAC) ⇒ BC ⊥ SC. (1)
Mặt khác SB ⊥ (P) nên SB ⊥ IJ (⊂ (P)) (2)
Từ (1) và (2) suy ra BCJI là tứ giác nội tiếp trong đường tròn đường kính BJ.
Ta có BC ⊥ (SAC) ⇒ BC ⊥ AJ (⊂ (SAC))
AJ ⊥ BC & AJ ⊥ SB (do SB ⊥ (P)) ⇒ AJ ⊥ (SBC) ⇒ AJ ⊥ JI (⊂ (SBC)) (3)
Lý luận tương tự, ta có:
BD ⊥ AD & BD ⊥ SA ⇒ BD ⊥ (SAD) ⇒ BD ⊥ AK (⊂ (SAD))
AK ⊥ BD & AK ⊥ SB(⊂ (P)) ⇒ AK ⊥ (SBD) ⇒ AK ⊥ KI. (4)
Từ (3) và (4) suy ra AKJI nội tiếp trong đường tròn đường kính AI nằm trong mặt phẳng (P).
b) Ta có ngay O’ là trung điểm BJ
Vì OO’ là đường trung bình của ΔABJ nên OO’ // AJ
Mà AJ ⊥ (SBC) nên OO’ ⊥ (SBC)
c) Ta có (SCD) ∩ (ABCD) = CD.
Gọi M = JK ∩ CD
SA ⊥ (ABCD) ⇒ SA ⊥ AM(⊂ (ABCD)) (5)
SB ⊥ (P) ⇒ SB ⊥ AM (⊂ (P)) (6)
Từ (5) và (6), ta có: AM ⊥ (SAB) ⇒ AM ⊥ AB.
Suy ra AM là tiếp tuyến của đường tròn ngoại tiếp ΔABC tại A. Như vậy AM cố định. Vì M = AM ∩ CD nên M cố định.
d) ΔAIB vuông tại I nên OA = OB = OI
ΔAJB vuông tại J (do AJ ⊥ (SBC)) nên OA = OB = OJ).
ΔAKB vuông tại K (do AK ⊥ (SBD)) nên OA = OB = OK).
Ta có OA = OB = OC = OD = OI = OJ = OK nên O là điểm cách đều các điểm đã cho và OA = AB/2 = a.
e) Theo chứng minh câu c.
f) Khi S thay đổi trên d, ta có I luôn nằm trong mặt phẳng (B, d).
Trong mặt phẳng này I luôn nhìn đoạn AB cố định dưới góc vuông nên tập hợp I là đường tròn ( C 1 ) đường kính AB nằm trong mặt phẳng (B, d).
Tương tự, tập hợp J là đường tròn ( C 2 ) đường kính AC nằm trong mặt phẳng (C, d) và tập hợp K là đường tròn đường kính AD nằm trong mặt phẳng (D, d).
Đúng 0
Bình luận (0)
Cho tứ giác ABCD thay đổi, luôn nội tiếp đường tròn bán kinh là căn bậc hai của 5 và có hai đường chéo vuông góc với nhau tại I sao cho IO = 1cm.Diện tích tam giác ICD đạt giá trị lớn nhất là ?
LÀM GIÚP CÂU D VỚI!Trên đường thẳng d cho các điểm A;B;C cố định.Đường tròn (O) thay đổi luôn qua B;C. Kẻ tiếp tuyến AE;AF. Gọi I là trung điểm của BC,N là trung điểm của EF. a) Chứng minh tứ giác AEOF nội tiếp đường tròn. b) Chứng minh E;F nằm trên 1 đường tròn cố định khi đường tròn (O) thay đổi. c) đường thẳng FI cắt đường tròn (O) tại M. Chứng minh EF // d . d) Chứng minh tâm đường tròn ngoại tiếp tam giác ONI luôn luôn thuộc đường thẳng cố định.
Đọc tiếp
LÀM GIÚP CÂU D VỚI!
Trên đường thẳng d cho các điểm A;B;C cố định.Đường tròn (O) thay đổi luôn qua B;C. Kẻ tiếp tuyến AE;AF. Gọi I là trung điểm của BC,N là trung điểm của EF.
a) Chứng minh tứ giác AEOF nội tiếp đường tròn.
b) Chứng minh E;F nằm trên 1 đường tròn cố định khi đường tròn (O) thay đổi.
c) đường thẳng FI cắt đường tròn (O) tại M. Chứng minh EF // d .
d) Chứng minh tâm đường tròn ngoại tiếp tam giác ONI luôn luôn thuộc đường thẳng cố định.
nó thuộc trung trực của một đường thẳng không đổi
Đúng 0
Bình luận (0)

