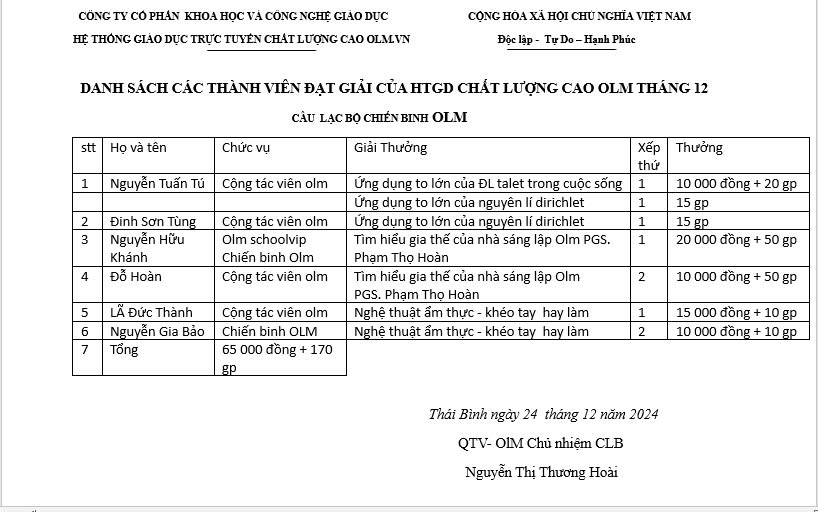
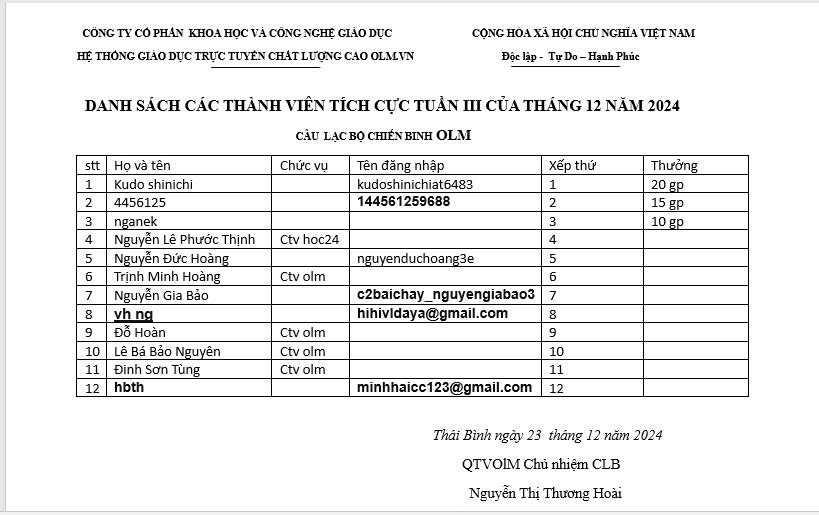
Danh sách thành viên đạt giải thưởng tuần III tháng 12 năm 2024
Cô Thương Hoài thân ái chào toàn thể các thành viên của Olm. Mừng ngày chúa giáng sinh, Hãy mở lòng và đón nhận những điều tốt đẹp nhất vì cô chắc rằng nó sẽ tới với các bạn. Nhất là những bạn có tên trong danh sách dưới đây. Hãy cùng nhau đua top bằng cách trả lời câu hỏi, giúp đỡ các bạn khác trên diễn đàn, tham gia các sự kiện của Olm. Để nhận thưởng, các em làm các yêu cầu sau:
Bình luận thứ nhất: Em đăng kí nhận giải thưởng:.......(tên giải thưởng)
Bình luận thứ hai: Em đăng kí nhận thưởng bằng:..... (xem danh sách )
(hai bình luận/ 1 giải thưởng)
Sau đó chat với cô qua Olm cung cấp số tài khoản ngân hàng, tên ngân hàng, chủ tài khoản để nhận thưởng.
Hạn nhận thưởng đến 24 giờ ngày 26 tháng 12 năm 2024. Sau thời gian này giải thưởng sẽ không còn hiệu lực.