Giúp mik bài này vs ạ

Giúp mik bài này vs ạ

\(a,\dfrac{x^2-1}{x^2+2x+1}=\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x+1\right)^2}\) (ĐK: \(x\ne-1\))
\(=\dfrac{x-1}{x+1}\)
Giá trị phân thức bằng 0 \(\Leftrightarrow x-1=0\Leftrightarrow x=1\)
\(b,\dfrac{x^2-5x+6}{x^2-4}=\dfrac{x^2-2x-3x+6}{\left(x-2\right)\left(x+2\right)}\) (ĐK: \(x\ne\pm2\))
\(=\dfrac{x\left(x-2\right)-3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x-2\right)\left(x-3\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x-3}{x+2}\)
Giá trị phân thức bằng 0 \(\Leftrightarrow x-3=0\Leftrightarrow x=3\)
Rút gọn rồi tính giá trị của biểu thức:
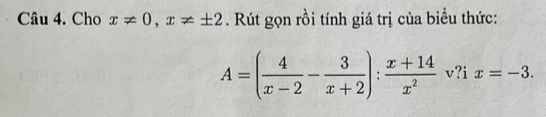
\(A=\dfrac{4x+8-3x+6}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x^2}{x+14}\)
\(=\dfrac{x+14}{x+14}\cdot\dfrac{x^2}{x^2-4}=\dfrac{x^2}{x^2-4}\)
Khi x=-3 thì \(A=\dfrac{\left(-3\right)^2}{\left(-3\right)^2-4}=\dfrac{9}{5}\)
Rút gọn biểu thức sau:
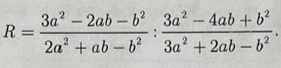
\(=\dfrac{3a^2-3ab+ab-b^2}{2a^2+2ab-ab-b^2}:\dfrac{3a^2-3ab-ab+b^2}{3a^2+3ab-ab-b^2}\)
\(=\dfrac{\left(a-b\right)\left(3a+b\right)}{\left(a+b\right)\left(2a-b\right)}\cdot\dfrac{\left(a+b\right)\left(3a-b\right)}{\left(a-b\right)\left(3a-b\right)}\)
\(=\dfrac{\left(3a+b\right)}{2a-b}\)
\(R=\dfrac{3a^2-2ab-b^2}{2a^2+ab-b^2}:\dfrac{3a^2-4ab+b^2}{3a^2+2ab-b^2}\)
\(R=\dfrac{3a^2-3ab+ab-b^2}{2a^2+2ab-ab-b^2}:\dfrac{3a^2-3ab-ab+b^2}{3a^2+3ab-ab-b^2}\)
\(R=\dfrac{\left(3a^2-3ab\right)+\left(ab-b^2\right)}{\left(2a^2+2ab\right)-\left(ab+b^2\right)}:\dfrac{\left(3a^2-3ab\right)-\left(ab-b^2\right)}{\left(3a^2+3ab\right)-\left(ab+b^2\right)}\)
\(R=\dfrac{3a\left(a-b\right)+b\left(a-b\right)}{2a\left(a+b\right)-b\left(a+b\right)}\cdot\dfrac{3a\left(a+b\right)-b\left(a+b\right)}{3a\left(a-b\right)-b\left(a-b\right)}\)
\(R=\dfrac{\left(a-b\right)\left(3a+b\right)}{\left(a+b\right)\left(2a-b\right)}\cdot\dfrac{\left(a+b\right)\left(3a-b\right)}{\left(a-b\right)\left(3a-b\right)}\)
\(R=\dfrac{\left(a-b\right)\left(3a+b\right)}{\left(a+b\right)\left(2a-b\right)}\cdot\dfrac{a+b}{a-b}\)
\(R=\dfrac{3a+b}{2a-b}\)
\(\dfrac{x}{x+2}+\dfrac{2}{x-2}=\dfrac{4x}{4-x^2}\)
ĐKXĐ: \(\dfrac{x}{x+2}+\dfrac{2}{x-2}=\dfrac{4x}{4-x^2}\) (ĐK: \(x\ne2,x\ne-2\))
\(\Leftrightarrow\dfrac{x}{x+2}+\dfrac{2}{x-2}=-\dfrac{4x}{x^2-4}\)
\(\Leftrightarrow\dfrac{x}{x+2}+\dfrac{2}{x-2}=-\dfrac{4x}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{x\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}+\dfrac{2\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=-\dfrac{4x}{\left(x+2\right)\left(x-2\right)}\)
\(\Leftrightarrow x\left(x-2\right)+2\left(x+2\right)=-4x\)
\(\Leftrightarrow x^2-2x+2x+4=-4x\)
\(\Leftrightarrow x^2+4=-4x\)
\(\Leftrightarrow x^2+4+4x=0\)
\(\Leftrightarrow x^2+2\cdot2\cdot x+2^2=0\)
\(\Leftrightarrow\left(x+2\right)^2=0\)
\(\Leftrightarrow x+2=0\)
\(\Leftrightarrow x=-2\left(ktmdk\right)\)
Vậy: \(x\in\varnothing\)
ĐKXĐ: x<>-2; x<>2
PT=>\(\dfrac{x^2-2x+2x+4}{\left(x+2\right)\left(x-2\right)}=\dfrac{-4x}{x^2-4}\)
=>x^2+4=-4x
=>x^2+4x+4=0
=>(x+2)^2=0
=>x+2=0
=>x=-2(loại)
a:
=> \(\dfrac{x-3}{5}=\dfrac{18-1+2x}{3}=\dfrac{2x+17}{3}\)
=>5(2x+17)=3(x-3)
=>10x+85=3x-9
=>7x=-94
=>x=-94/7
b: \(\Leftrightarrow\dfrac{15\cdot\left(x-3\right)}{20}+\dfrac{2\left(4x-10.5\right)}{20}=\dfrac{12\left(x+1\right)}{20}+\dfrac{120}{20}\)
=>15(x-3)+2(4x-10,5)=12(x+1)+20
=>15x-45+8x-21=12x+32
=>23x-66=12x+32
=>11x=98
=>x=98/11
c:
ĐKXĐ: x<>1; x<>-1
\(\dfrac{3}{1+x}+\dfrac{2}{x-1}=\dfrac{5x}{1-x^2}\)
=>\(\dfrac{3\left(x-1\right)+2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5x}{x^2-1}\)
=>3x-3+2x+2=-5x
=>5x-1=-5x
=>10x=1
=>x=1/10(nhận)
Rút gọn rồi tính giá trị của biểu thức sau:
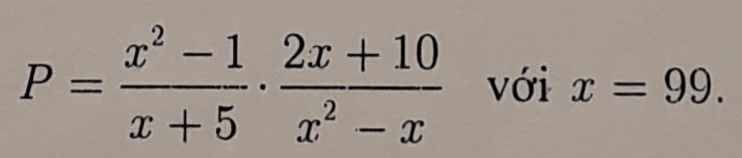
\(P=\dfrac{x^2-1}{x+5}\cdot\dfrac{2x+10}{x^2-x}\) (ĐK: \(x\ne-1,x\ne0,x\ne1\))
\(P=\dfrac{\left(x-1\right)\left(x+1\right)}{x+5}\cdot\dfrac{2\left(x+5\right)}{x\left(x-1\right)}\)
\(P=\dfrac{2\left(x-1\right)\left(x+1\right)\left(x+5\right)}{x\left(x+5\right)\left(x-1\right)}\)
\(P=\dfrac{2\left(x+1\right)}{x}\)
Thay \(x=99\left(tm\right)\) vào P ta có:
\(P=\dfrac{2\left(99+1\right)}{99}=\dfrac{2\cdot100}{99}=\dfrac{200}{99}\)
\(P=\dfrac{x^2-1}{x+5}\cdot\dfrac{2x+10}{x^2-x}\\ =\dfrac{\left(x^2-1\right)\left(2x+10\right)}{\left(x+5\right)\left(x^2-x\right)}\\ =\dfrac{\left(x+1\right)\left(x-1\right)\left(x+5\right)2}{\left(x+5\right)\left(x-1\right)x}\\ =\dfrac{2x+2}{x}\)
Thay \(x=99\) vào P ta có
\(P=\dfrac{2.99+2}{99}\\ =\dfrac{200}{99}\)
Vậy \(x=99\) thì \(P=\)\(\dfrac{200}{99}\)
6:
a: a+b+c=0
=>a=-b-c; b=-a-c; c=-a-b
=>a^2=(b+c)^2; b^2=(a+c)^2; c^2=(a+b)^2
=>4bc-a^2=4bc-(b+c)^2=-(b-c)^2; 4ac-b^2=-(a-c)^2; 4ab-c^2=-(a-b)^2
\(M=\dfrac{-\left(b-c\right)^2}{bc+2a^2}\cdot\dfrac{-\left(a-c\right)^2}{ca+2b^2}\cdot\dfrac{-\left(a-b\right)^2}{ab+2c^2}\)
\(=-\dfrac{\left(b-c\right)^2}{2b^2+4bc+2c^2+bc}\cdot\dfrac{\left(a-c\right)^2}{2a^2+4ac+2c^2+ac}\cdot\dfrac{\left(a-b\right)^2}{2a^2+4ab+2b^2+ab}\)
\(=\dfrac{-\left(b-c\right)^2}{2b\left(b+2c\right)+c\left(b+2c\right)}\cdot\dfrac{\left(a-c\right)^2}{2a\left(2c+a\right)+c\left(2c+a\right)}\cdot\dfrac{\left(a-b\right)^2}{2a\left(2b+a\right)+b\left(2a+b\right)}\)
\(=\dfrac{-\left(b-c\right)^2}{\left(b+2c\right)\left(2b+c\right)}\cdot\dfrac{\left(a-c\right)^2}{\left(2a+c\right)\left(2c+a\right)}\cdot\dfrac{\left(a-b\right)^2}{\left(2b+a\right)\left(2a+b\right)}\)
\(=\dfrac{-\left(b-c\right)^2}{\left(-a-c+2c\right)\left(2b-a-b\right)}\cdot\dfrac{\left(a-c\right)^2}{\left(2a-a-b\right)\left(2c-b-c\right)}\cdot\dfrac{\left(a-b\right)^2}{\left(2b-b-c\right)\left(2a-a-c\right)}\)
\(=\dfrac{-\left(b-c\right)^2}{\left(c-a\right)\left(b-a\right)}\cdot\dfrac{\left(a-c\right)^2}{\left(a-b\right)\left(c-b\right)}\cdot\dfrac{\left(a-b\right)^2}{\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{-\left(b-c\right)^2\left(a-c\right)^2\left(a-b\right)^2}{-\left(a-b\right)^2\cdot\left[-\left(a-c\right)^2\right]\cdot\left[-\left(b-c\right)^2\right]}\)
=1
b: \(N=\dfrac{a+b}{b}\cdot\dfrac{b+c}{c}\cdot\dfrac{a+c}{a}=\dfrac{\left(-c\right)\cdot\left(-a\right)\cdot\left(-b\right)}{abc}=-1\)
a) \(=\dfrac{\left(12x+5\right)\left(4x+3\right)}{30\left(x+9\right)\left(12x+5\right)}+\dfrac{\left(12x+5\right)\left(6-3x\right)}{30\left(x+9\right)\left(12x+5\right)}\)
\(=\dfrac{4x+3-3x+6}{30\left(x+9\right)}\)
\(=\dfrac{1}{30}\)
Thu gọn biểu thức sau:
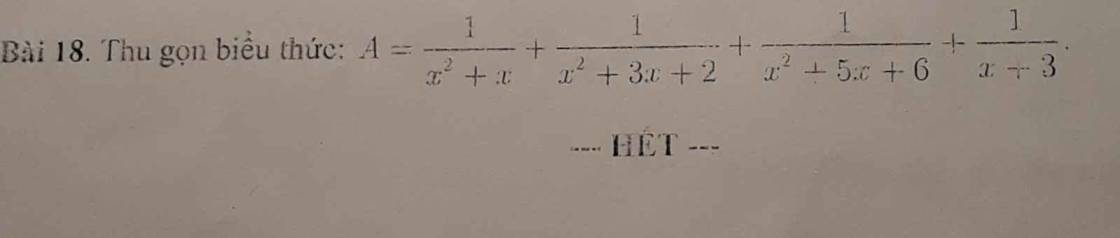
\(A=\dfrac{1}{x^2+x}+\dfrac{1}{x^2+3x+2}+\dfrac{1}{x^2+5x+6}+\dfrac{1}{x+3}\) (ĐK: \(x\ne-1;x\ne0;x\ne-2;x\ne-3\))
\(A=\dfrac{1}{x\left(x+1\right)}+\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{x+3}\)
\(A=\dfrac{\left(x+2\right)\left(x+3\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}+\dfrac{x\left(x+3\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}+\dfrac{x\left(x+1\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}+\dfrac{x\left(x+1\right)\left(x+2\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)\(A=\dfrac{x^2+5x+6+x^2+3x+x^2+x+x^3+2x^2+x^2+2x}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{x^3+6x^2+11x+6}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{x^3+5x^2+6x+x^2+5x+6}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{x\left(x+5x+6\right)+\left(x^2+5x+6\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{\left(x^2+5x+6\right)\left(x+1\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{\left(x+1\right)\left(x+2\right)\left(x+3\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{1}{x}\)