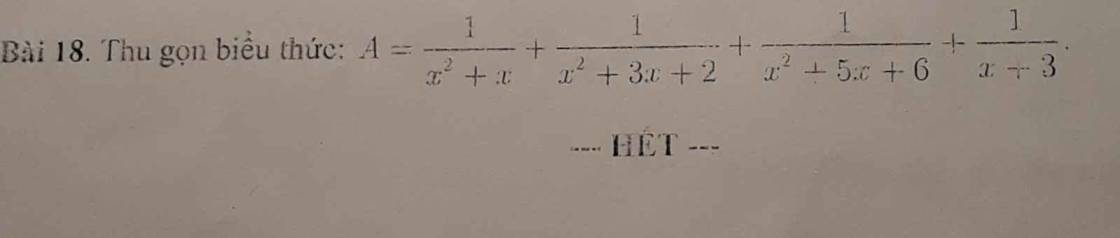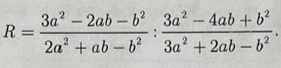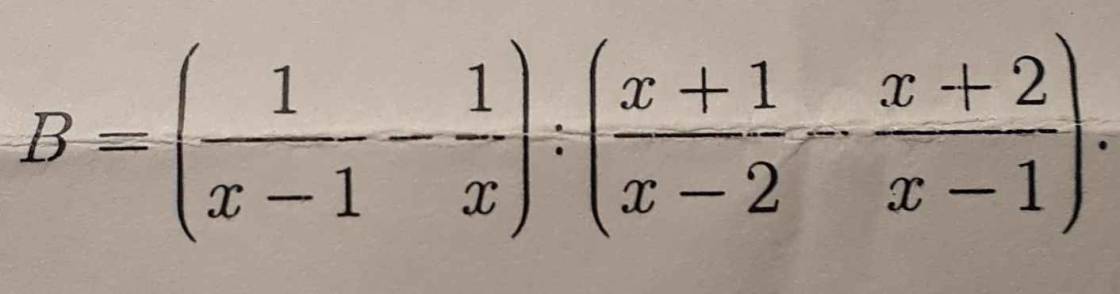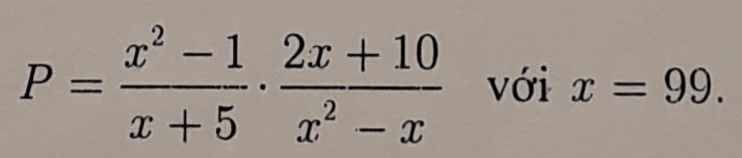\(A=\dfrac{1}{x^2+x}+\dfrac{1}{x^2+3x+2}+\dfrac{1}{x^2+5x+6}+\dfrac{1}{x+3}\) (ĐK: \(x\ne-1;x\ne0;x\ne-2;x\ne-3\))
\(A=\dfrac{1}{x\left(x+1\right)}+\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{x+3}\)
\(A=\dfrac{\left(x+2\right)\left(x+3\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}+\dfrac{x\left(x+3\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}+\dfrac{x\left(x+1\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}+\dfrac{x\left(x+1\right)\left(x+2\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)\(A=\dfrac{x^2+5x+6+x^2+3x+x^2+x+x^3+2x^2+x^2+2x}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{x^3+6x^2+11x+6}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{x^3+5x^2+6x+x^2+5x+6}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{x\left(x+5x+6\right)+\left(x^2+5x+6\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{\left(x^2+5x+6\right)\left(x+1\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{\left(x+1\right)\left(x+2\right)\left(x+3\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{1}{x}\)