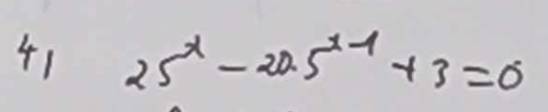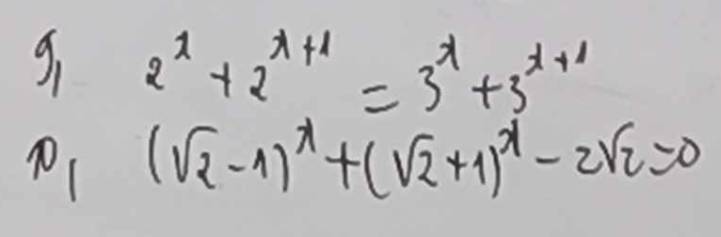\((\log_{2} (4x))^2-\log_{\sqrt{}2} (2x)=5\)
Ôn tập cuối năm môn Đại số 11
\(\left[log_24x\right]^2-log_{\sqrt{2}}2x=5\)
=>\(\left[log_2\left(2\cdot2x\right)\right]^2-log_{2^{\dfrac{1}{2}}}2x=5\)
=>\(\left[1+log_22x\right]^2-1:\dfrac{1}{2}\cdot log_22x=5\)
=>\(\left(log_22x\right)^2+2\cdot log_22x+1-2\cdot log_22x=5\)
=>\(\left(log_22x\right)^2=4\)
=>\(\left[{}\begin{matrix}log_22x=2\\log_22x=-2\left(loại\right)\end{matrix}\right.\Leftrightarrow log_22x=2\)
=>\(2x=2^2=4\)
=>x=2
Đúng 1
Bình luận (0)
logx2 + log2x ≥ \(5/2\)
ĐKXĐ: x>0
Đặt \(a=log_x2\left(a>=0\right)\)
BPT sẽ trở thành \(a+\dfrac{1}{a}>=\dfrac{5}{2}\)
=>\(\dfrac{a^2+1}{a}>=\dfrac{5}{2}\)
=>\(2\left(a^2+1\right)>=5a\)
=>\(2a^2-5a+2>=0\)
=>\(\left(2a-1\right)\left(a-2\right)>=0\)
=>\(\left[{}\begin{matrix}a>=2\\a< =\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}a>=2\\0< a< =\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}log_x2>=2\\0< log_x2< =\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x>=\sqrt{2}\\0< x< =4\end{matrix}\right.\)
Đúng 1
Bình luận (0)
\(25^x-20\cdot5^{x-1}+3=0\)
=>\(\left(5^x\right)^2-20\cdot\dfrac{5^x}{5}+3=0\)
=>\(\left(5^x\right)^2-4\cdot5^x+3=0\)
=>\(\left(5^x-3\right)\left(5^x-1\right)=0\)
=>\(\left[{}\begin{matrix}5^x-3=0\\5^x-1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}5^x=3\\5^x=1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=log_53\\x=0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
10: \(\left(\sqrt{2}-1\right)^x+\left(\sqrt{2}+1\right)^x-2\sqrt{2}=0\)
=>\(\dfrac{1}{\left(\sqrt{2}+1\right)^x}+\left(\sqrt{2}+1\right)^x-2\sqrt{2}=0\)(1)
Đặt \(a=\left(\sqrt{2}+1\right)^x\)(a>0)
Phương trình (1) sẽ trở thành \(\dfrac{1}{a}+a-2\sqrt{2}=0\)
=>\(\dfrac{a^2+1-2\sqrt{2}\cdot a}{a}=0\)
=>\(a^2-2\sqrt{2}\cdot a+1=0\)
=>\(a^2-2\sqrt{2}a+2-1=0\)
=>\(\left(a-\sqrt{2}\right)^2=1\)
=>\(\left[{}\begin{matrix}a=\sqrt{2}+1\left(nhận\right)\\a=\sqrt{2}-1\left(nhận\right)\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left(\sqrt{2}+1\right)^x=\sqrt{2}+1\\\left(\sqrt{2}+1\right)^x=\sqrt{2}-1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
1) log3(2x-1)=4
\(log_3\left(2^x-1\right)=4\)
=>\(2^x-1=3^4=81\)
=>\(2^x=82\)
=>\(x=log_282\)
Đúng 0
Bình luận (0)
1) 4x+2x+1-3=0
\(4^x+2^{x+1}-3=0\)
=>\(\left(2^x\right)^2+2\cdot2^x-3=0\)
=>\(\left(2^x+3\right)\left(2^x-1\right)=0\)
mà \(2^x+3>0\forall x\)
nên \(2^x-1=0\)
=>\(2^x=1\)
=>x=0
Đúng 1
Bình luận (0)
1. 3x+9.3-x=10
\(3^x+9\cdot3^{-x}=10\)
=>\(3^x+\dfrac{9}{3^x}=10\)
=>\(\dfrac{\left(3^x\right)^2+9}{3^x}=10\)
=>\(\left(3^x\right)^2+9=10\cdot3^x\)
=>\(\left(3^x\right)^2-10\cdot3^x+9=0\)
=>\(\left(3^x-1\right)\left(3^x-9\right)=0\)
=>\(\left[{}\begin{matrix}3^x-1=0\\3^x-9=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}3^x=1\\3^x=9\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm \(x\) biết:
\(\left(\sqrt{3}\right)^x=243\)
\(0,1^x=1000\)
\(\left(\dfrac{1}{2}\right)^x=1024\)
\(\left(0,2\right)^{x+3}< \dfrac{1}{5}\)
\(\left(\dfrac{3}{5}\right)^{2x+1}>\left(\dfrac{5}{3}\right)^2\)
\(5^{x-1}+5^{x+2}=3\)
a: \(\left(\sqrt{3}\right)^x=243\)
=>\(3^{\dfrac{1}{2}\cdot x}=3^5\)
=>\(\dfrac{1}{2}\cdot x=5\)
=>x=10
b: \(0,1^x=1000\)
=>\(\left(\dfrac{1}{10}\right)^x=1000\)
=>\(10^{-x}=10^3\)
=>-x=3
=>x=-3
c: \(\left(0,2\right)^{x+3}< \dfrac{1}{5}\)
=>\(\left(0,2\right)^{x+3}< 0,2\)
=>x+3>1
=>x>-2
d: \(\left(\dfrac{3}{5}\right)^{2x+1}>\left(\dfrac{5}{3}\right)^2\)
=>\(\left(\dfrac{3}{5}\right)^{2x+1}>\left(\dfrac{3}{5}\right)^{-2}\)
=>2x+1<-2
=>2x<-3
=>\(x< -\dfrac{3}{2}\)
e: \(5^{x-1}+5^{x+2}=3\)
=>\(5^x\cdot\dfrac{1}{5}+5^x\cdot25=3\)
=>\(5^x=\dfrac{3}{25,2}=\dfrac{1}{8,4}=\dfrac{10}{84}=\dfrac{5}{42}\)
=>\(x=log_5\left(\dfrac{5}{42}\right)=1-log_542\)
Đúng 1
Bình luận (0)
Cho \(a>0\), \(a\ne1\). Rút gọn biểu thức \(A=\left(\ln a+\log_ae\right)^2+\ln^2a-\log^2_ae\) bằng.
Em không thấy chủ đề của Logarit ạ :<
\(A=\left(lna+log_{\alpha}e\right)^2+ln^2a-\log_a^2e\)
\(=ln^2a+\log_{\alpha}^2e+2\cdot lna\cdot\log_{\alpha}e+ln^2a-\log_{\alpha}^2e\)
\(=2\cdot\log_e^2\alpha+2\cdot\log_e\alpha\cdot\log_{\alpha}e\)
\(=2\cdot ln^2\alpha+2\)
Đúng 1
Bình luận (0)
2. Cho h/c đều SABC có AB=2a.
a) Góc giữa cạnh bên và đáy = 60o. Tính VSABC
b) Góc giữa mặt bên và đáy = 30o .Tính VSABC