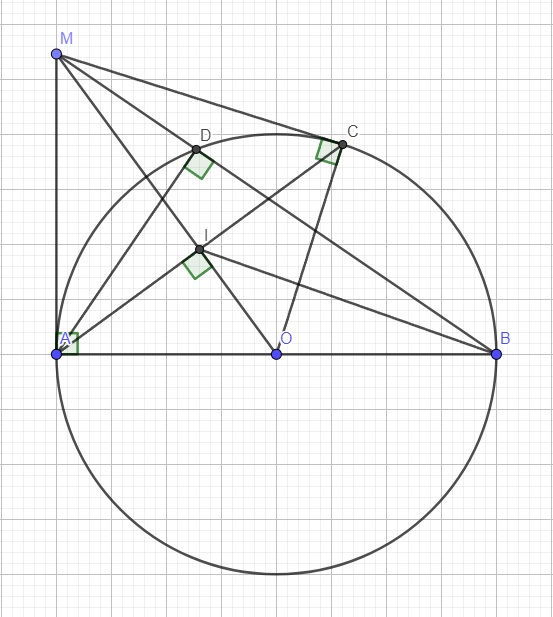
cho đường tròn tâm O ,đường kính AB .Trên tia tiếp tuyến Ax của đường trong (O) lấy điểm M(M khác A), kể tiếp tuyến MC với đường tròn (O)(C là tiếp điểm).(yêu cầu vẽ hình)
a)Chứng minh bốn điểm O,A,M,C cùng thuộc 1 đường tròn
b)chứng minh OM\(\perp\)AC tại I
c)Tia BM cắt đường tròn (O) tại D (D ≠ B).chứng minh :MA2 =MI.MO=MD.MB
d)chứng minh:góc OIB = góc OBM\(\)