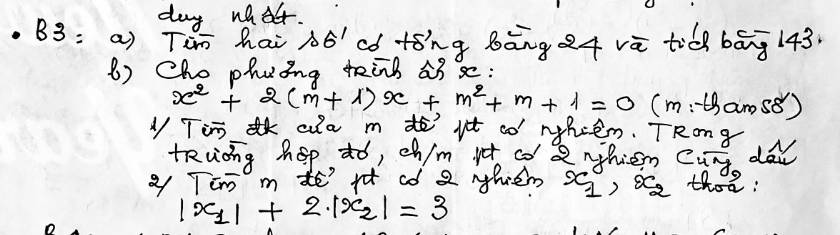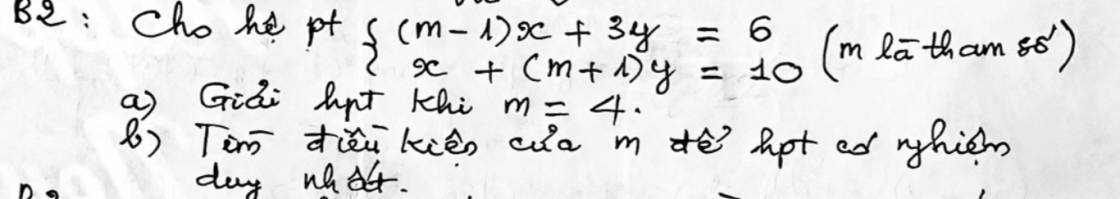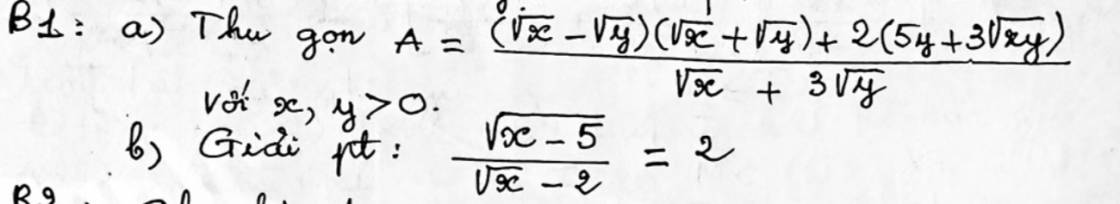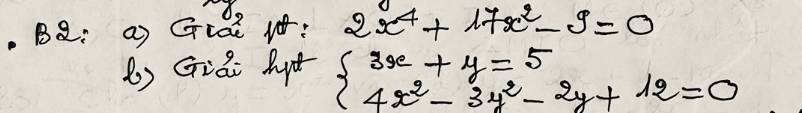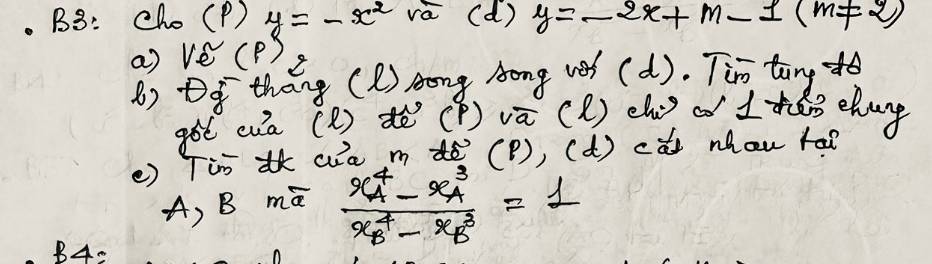Chương IV - Hàm số y = ax^2 (a khác 0). Phương trình bậc hai một ẩn

- Gọi giá niếm yết của mặt hàng A là x (đồng) (x∈N*)

- Giá bán của mặt hàng A sau khi khuyến mãi đợt 1: \(\left(100\%-30\%\right)x=70\%x\) (đồng)

- Giá bán của mặt hàng A sau khi khuyến mãi đợt 2:

\(70\%x.\left(100\%+25\%\right)=0,875x\) (đồng)

Vì giá bán của mặt hàng A ở đợt 2 là 280 000 đồng nên ta có phương trình:

\(0,875x=280000\Leftrightarrow x=320000\) (nhận)

Vậy giá niêm yết của mặt hàng A là 320 000 đồng.

Phương trình hoành độ giao điểm (P) và ( d) có : 

\(x^2=2mx-2m+2\)

\(x^2-2mx+2m-2=0\left(1\right)\)

\(\Delta'=m^2-2m+2=\left(m-1\right)^2+1>0\forall m.\)

⇒ ( P) cắt ( d) tại hai điểm phân biệt 

Theo viét : \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=2m-2\end{matrix}\right.\)

Ta có : \(x_1^2-21=6x_1x_2-x^2_2\Leftrightarrow\left(x_1+x_2\right)^2-8x_1x_2-21=0\)\(\Leftrightarrow4m^2-16m+16-21=0\Leftrightarrow4m^2-16m-5=0\)

\(\Delta'=8^2+4.5=84>0\Rightarrow\sqrt{\Delta'}=2\sqrt{21}\)

⇒ Phương trình hai nghiệm phân biệt 

\(m_1=\dfrac{4+\sqrt{21}}{2};m_2=\dfrac{4-\sqrt{21}}{2}\)

 Vậy....

a.

Theo hệ quả của định lý Viet, 2 số đã cho là nghiệm của pt:

\(x^2-24x+143=0\)

\(\Rightarrow\left[{}\begin{matrix}x=13\\x=11\end{matrix}\right.\)

Vậy 2 số đó là 11 và 13

b.

1.

\(\Delta'=\left(m+1\right)^2-\left(m^2+m+1\right)=m\)

Phương trình có nghiệm khi \(\Delta\ge0\Rightarrow m\ge0\)

Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2\left(m+1\right)\\x_1x_2=m^2+m+1\end{matrix}\right.\)

Do \(x_1x_2=m^2+m+1=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0;\forall m\) nên pt đã cho có 2 nghiệm cùng dấu

2. Do pt có 2 nghiệm cùng dấu, mà \(m\ge0\Rightarrow x_1+x_2=-2\left(m+1\right)< 0\)

\(\Rightarrow\left\{{}\begin{matrix}x_1< 0\\x_2< 0\end{matrix}\right.\)

\(\Rightarrow\left|x_1\right|+2\left|x_2\right|=3\Rightarrow-x_1-2x_2=3\)

\(\Rightarrow x_1+2x_2=-3\)

Kết hợp \(x_1+x_2=-2\left(m+1\right)\Rightarrow\left\{{}\begin{matrix}x_1+x_2=-2\left(m+1\right)\\x_1+2x_2=-3\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x_2=2m-1\\x_1=-4m-1\end{matrix}\right.\)

Thế vào \(x_1x_2=m^2+m+1\)

\(\Rightarrow\left(2m-1\right)\left(-4m-1\right)=m^2+m+1\)

\(\Leftrightarrow9m^2-m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{1}{9}\end{matrix}\right.\) (thỏa mãn)

a. Em tự giải

b. Hệ có nghiệm duy nhất khi:

\(\dfrac{m-1}{1}\ne\dfrac{3}{m+1}\)

\(\Rightarrow\left(m-1\right)\left(m+1\right)\ne3\)

\(\Rightarrow m^2\ne4\)

\(\Rightarrow m\ne\pm2\)

a.

\(A=\dfrac{x-y+10y+6\sqrt{xy}}{\sqrt{x}+3\sqrt{y}}=\dfrac{x+6\sqrt{xy}+9y}{\sqrt{x}+3\sqrt{y}}\)

\(=\dfrac{\left(\sqrt{x}+3\sqrt{y}\right)^2}{\sqrt{x}+3\sqrt{y}}=\sqrt{x}+3\sqrt{y}\)

b.

ĐKXĐ: \(x\ge5\)

\(\dfrac{\sqrt{x-5}}{\sqrt{x}-2}=2\Rightarrow\sqrt{x-5}=2\sqrt{x}-4\)

\(\Leftrightarrow\sqrt{x-5}+4=2\sqrt{x}\)

\(\Leftrightarrow x-5+16+8\sqrt{x-5}=4x\)

\(\Leftrightarrow8\sqrt{x-5}=3x-11\)

\(\Rightarrow64\left(x-5\right)=\left(3x-11\right)^2\)

\(\Leftrightarrow9x^2-130x+441=0\Rightarrow\left[{}\begin{matrix}x=9\\x=\dfrac{49}{9}\end{matrix}\right.\) (thỏa mãn)

a: =>2x^4+18x^2-x^2-9=0

=>(x^2+9)(2x^2-1)=0

=>2x^2=1

=>x^2=1/2

=>\(x=\pm\dfrac{\sqrt{2}}{2}\)

b: =>y=5-3x và 4x^2-3(5-3x)^2-2(5-3x)+12=0(1)

(1) suy ra 4x^2-3(9x^2-30x+25)-10+6x+12=0

=>4x^2-27x^2+90x-75+6x+2=0

=>-23x^2+96x-73=0

=>x=1 hoặc x=73/23

=>y=2 hoặc y=-104/23

a: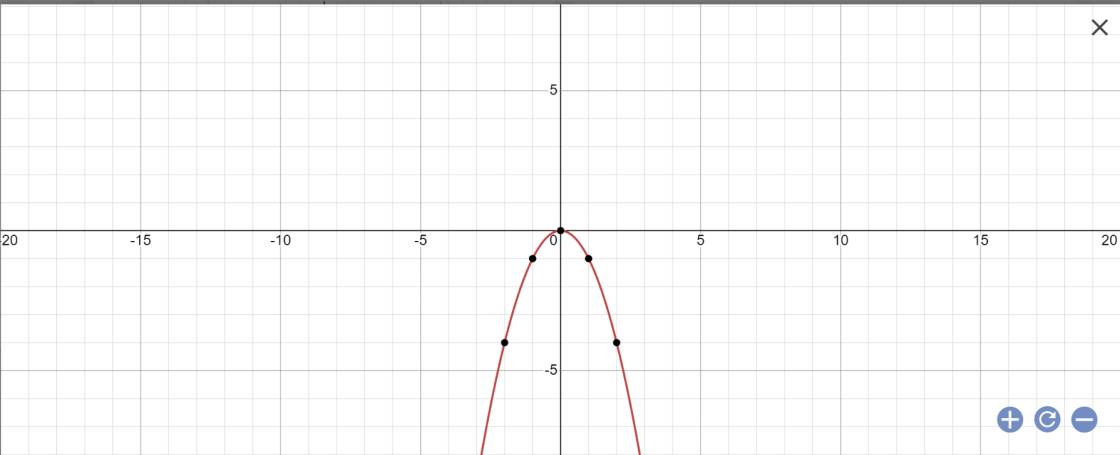 

b: (l)//(d) nên l: y=-2x+a

PTHĐGĐ là:

-x^2+2x-a=0

=>x^2-2x+a=0

Để (L) tiếp xúc (P) thì (-2)^2-4*1*a=0

=>a=1

\(a,\) Tự vẽ nha

\(b,\) Gọi \(A\left(x_A;y_A\right)\) ; \(B\left(x_B;y_B\right)\) là tọa độ giao điểm của (P) và (D)

Ta có : 

\(-x^2=x-2\)

\(\Leftrightarrow-x^2-x+2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_1=1\\x_2=-2\end{matrix}\right.\)

Thay \(x_1=1\) vào (p) : \(y=-x^2\Rightarrow y=-1^2=-1\)

Thay \(x_2=-2\) vào (d) : \(y=x-2\Rightarrow y=-2-2=-4\)

Vậy tọa độ của 2 đồ thị hs là : \(A\left(1;-1\right);B\left(-2;-4\right)\)

a: Hàm số đồng biến khi x>0 và nghịch biến khi x<0

b: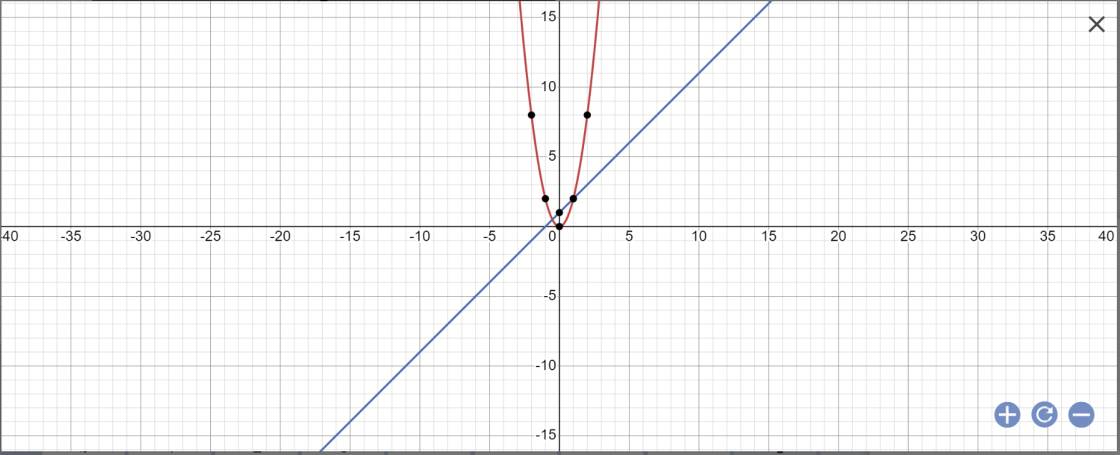 

c: PTHĐGĐ là:

2x^2=x+1

=>2x^2-x-1=0

=>2x^2-2x+x-1=0

=>(x-1)(2x+1)=0

=>x=1 hoặc x=-1/2

=>y=2 hoặc y=1/2