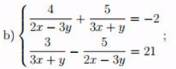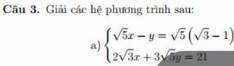Chương III - Hệ hai phương trình bậc nhất hai ẩn

Bài 5:

a: Xét (O) có

ΔADB nội tiếp

AB là đường kính

Do đó: ΔADB vuông tại D

=>AD\(\perp\)DB tại D

=>AD\(\perp\)BC tại D

Xét ΔABC vuông tại A có AD là đường cao

nên \(AC^2=CD\cdot CB\)

b: Ta có: ΔOAE cân tại O

mà OC là đường cao

nên OC là phân giác của góc AOE

Xét ΔOAC và ΔOEC có

OA=OE

\(\widehat{AOC}=\widehat{EOC}\)

OC chung

Do đó: ΔOAC=ΔOEC

=>\(\widehat{OAC}=\widehat{OEC}\)

mà \(\widehat{OAC}=90^0\)

nên \(\widehat{OEC}=90^0\)

=>CE là tiếp tuyến của (O)

Bài 3:

a: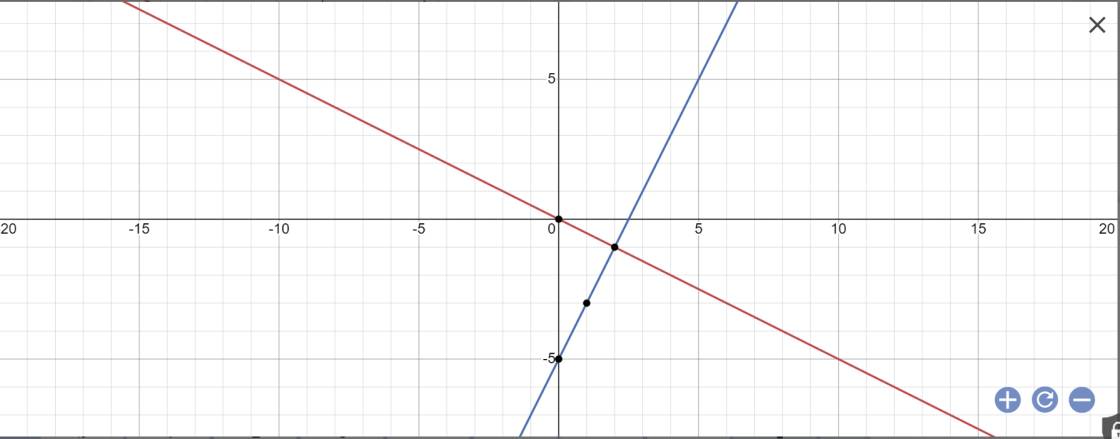 

b: Phương trình hoành độ giao điểm là:

\(-\dfrac{1}{2}x=2x-5\)

=>\(-\dfrac{1}{2}x-2x=-5\)

=>\(-\dfrac{5}{2}x=-5\)

=>x=2

Thay x=2 vào y=-1/2x, ta được:

\(y=-\dfrac{1}{2}\cdot2=-1\)

Vậy: (d) cắt (d') tại điểm A(2;-1)

Để (d1) cắt (d2) tại một điểm nằm trên trục tung thì

\(\left\{{}\begin{matrix}m-2\ne-1\\m^2+2=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m\ne1\\m^2=1\end{matrix}\right.\Leftrightarrow m=-1\)

Lời giải:

ĐKXĐ: $x\geq 3$
PT $\Leftrightarrow \sqrt{9(x-3)}+\sqrt{x-3}=6+\frac{1}{2}\sqrt{4(x-3)}$

$\Leftrightarrow 3\sqrt{x-3}+\sqrt{x-3}=6+\sqrt{x-3}$

$\Leftrightarrow 3\sqrt{x-3}=6$

$\Leftrightarrow \sqrt{x-3}=2$
$\Leftrightarrow x-3=4$

$\Leftrightarrow x=7$ (tm)

Lần sau bạn lưu ý gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.

\(\lim\limits\dfrac{2n^2+1}{n^2+1}=\lim\limits\dfrac{2+\dfrac{1}{n^2}}{1+\dfrac{1}{n^2}}=\dfrac{2+0}{1+0}=\dfrac{2}{1}=2\)

b: \(\left\{{}\begin{matrix}\dfrac{4}{2x-3y}+\dfrac{5}{3x+y}=-2\\\dfrac{3}{3x+y}-\dfrac{5}{2x-3y}=21\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{4}{2x-3y}+\dfrac{5}{3x+y}=-2\\\dfrac{5}{2x-3y}-\dfrac{3}{3x+y}=-21\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{12}{2x-3y}+\dfrac{15}{3x+y}=-6\\\dfrac{25}{2x-3y}-\dfrac{15}{3x+y}=-105\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{37}{2x-3y}=-111\\\dfrac{12}{2x-3y}+\dfrac{15}{3x+y}=-6\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\\dfrac{15}{3x+y}=-6-\dfrac{12}{2x-3y}=-6-12:\dfrac{-1}{3}=-6+36=30\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\3x+y=\dfrac{1}{2}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\9x+3y=\dfrac{3}{2}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}11x=-\dfrac{1}{3}+\dfrac{3}{2}=\dfrac{-2+9}{6}=\dfrac{7}{6}\\2x-3y=-\dfrac{1}{3}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{7}{66}\\3y=2x+\dfrac{1}{3}=\dfrac{7}{33}+\dfrac{1}{3}=\dfrac{7+11}{33}=\dfrac{18}{33}=\dfrac{6}{11}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{7}{66}\\y=\dfrac{2}{11}\end{matrix}\right.\)

giúp mik với

Gọi \(\left\{{}\begin{matrix}\dfrac{1}{2x-3y}=A\\\dfrac{1}{3x+y}=B\end{matrix}\right.\)

Hệ đây nha

\(\left\{{}\begin{matrix}4A+5B=2\\3B-5A=21\end{matrix}\right.\)

xong giải hệ như bình thường

giải A,B xong r thay kết quả 

\(\left\{{}\begin{matrix}\dfrac{1}{x}=KếtquảcủaA\\\dfrac{1}{y}=kếtquảcủaB\end{matrix}\right.\)

Nếu tử =1 thì bằng luôn kết quả

Nếu tử \(\ne1\) thì nhân chéo

Sau đó lại giải hệ lần 2 và kế luật

\(\left\{{}\begin{matrix}\sqrt{5}x-y=\sqrt{5}\left(\sqrt{3}-1\right)\\2\sqrt{3}\cdot x+3\sqrt{5}y=21\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3\sqrt{5}\cdot x\sqrt{5}-3\sqrt{5}\cdot y=3\sqrt{5}\cdot\sqrt{5}\left(\sqrt{3}-1\right)\\2\sqrt{3}\cdot x+3\sqrt{5}y=21\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}15x-3\sqrt{5}\cdot y=15\left(\sqrt{3}-1\right)\\2\sqrt{3}\cdot x+3\sqrt{5}y=21\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x\left(15+2\sqrt{3}\right)=15\sqrt{3}-15+21\\2\sqrt{3}\cdot x+3\sqrt{5}\cdot y=21\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{15\sqrt{3}+6}{15+2\sqrt{3}}=\sqrt{3}\\2\sqrt{3}\cdot x+3\sqrt{5}\cdot y=21\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\sqrt{3}\\y\cdot3\sqrt{5}+12=21\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\sqrt{3}\\y\cdot3\sqrt{5}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{3}\\y=\dfrac{3}{\sqrt{5}}=\dfrac{3\sqrt{5}}{5}\end{matrix}\right.\)

a) \(\left\{{}\begin{matrix}\sqrt{5}x-y=\sqrt{5}\left(\sqrt{3}-1\right)\\2\sqrt{3}x+3\sqrt{5}y=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{5}x-y=\sqrt{15}-\sqrt{5}\\2\sqrt{3}x+3\sqrt{5}y=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=\sqrt{3}-1\\2\sqrt{3}x+3\sqrt{5}y=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{3}x-2\sqrt{3}y=\sqrt{3}-1\\2\sqrt{3}x-3\sqrt{5}y=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2\sqrt{3}y=\sqrt{3}-22\\x-y=\sqrt{3}-1\end{matrix}\right.\left\{{}\begin{matrix}y=-24\\x-y=\sqrt{3}-1\end{matrix}\right.\left\{{}\begin{matrix}y=-24\\x+24=\sqrt{3}-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-24\\x=\sqrt{3}-25\end{matrix}\right.\left\{{}\begin{matrix}y=-24\\x=\sqrt{3}-\sqrt{\text{6}25}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-24\\x=-\sqrt{\text{6}22}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-24\\x\approx-25\end{matrix}\right.\left\{{}\begin{matrix}x\approx-25\\y=-24\end{matrix}\right.\)

a: \(\left\{{}\begin{matrix}x+2y=3\\4x+5y=6\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4x+8y=12\\4x+5y=6\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3y=6\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=3-2y=3-2\cdot2=-1\end{matrix}\right.\)

b: \(\left\{{}\begin{matrix}x+y=5\\2x-y=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x+y+2x-y=5+4\\x+y=5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x=9\\x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=5-3=2\end{matrix}\right.\)

c: \(\left\{{}\begin{matrix}x+2y=5\\x-5y=-9\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x+2y-x+5y=5+9=14\\x+2y=5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}7y=14\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=5-2y=1\end{matrix}\right.\)

a: AC=AD+DC

=3+5

=8(cm)

Xét ΔBAC có BD là phân giác

nên \(\dfrac{AB}{AD}=\dfrac{CB}{CD}\)

=>\(\dfrac{AB}{3}=\dfrac{CB}{5}=k\)

=>AB=3k; CB=5k

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(\left(5k\right)^2=\left(3k\right)^2+8^2\)

=>\(16k^2=64\)

=>\(k^2=4\)

=>k=2

=>AB=3*2=6cm; BC=2*5=10(cm)

b: Xét ΔBAC có BE là phân giác góc ngoài tại B

nên \(\dfrac{EA}{EC}=\dfrac{BA}{BC}\)

=>\(\dfrac{EA}{EC}=\dfrac{3}{5}\)

=>\(\dfrac{EA}{3}=\dfrac{EC}{5}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{EC}{5}=\dfrac{EA}{3}=\dfrac{EC-EA}{5-3}=\dfrac{AC}{2}=\dfrac{8}{2}=4\)

=>EA=12(cm)

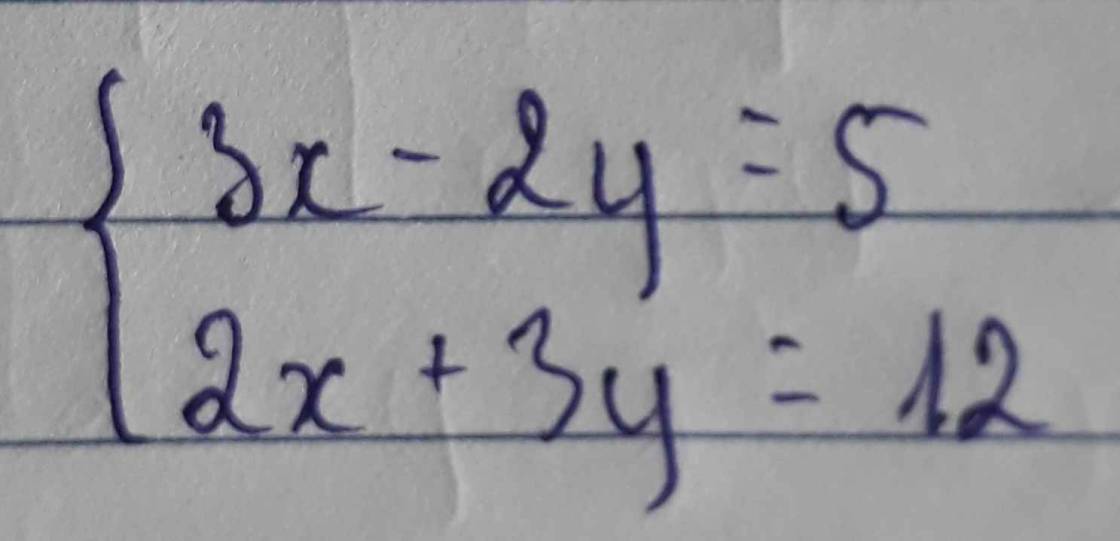
3x - 2y = 5 ⇔ 6x - 4y = 10

và 2x + 3y = 12 ⇔ 6x + 9y = 36

⇔ 13y = 26

và 2x + 3y = 12

⇔ y = 2

và 2x + 3.2 = 12

⇔ y = 2

và 2x = 6

⇔ y = 2

và x = 3

Vậy S = {(3; 2)}

\(\left\{{}\begin{matrix}2x+y=3\\3x+2y=2\end{matrix}\right.\)

Từ `(1)` : `2x+y=3=> y=3-2x` thế vào `(2)`

Ta được :

`3x+2(3-2x)=2`

`<=> 3x+6-4x=2`

`<=> -x =-4`

`<=>x=4`

`=> y= 3-2.4`

`<=> y= 3-6`

`<=>y=-3`

Vậy nghiệm của hệ `(x,y)` là `(4;-3)`