Chương III - Hệ hai phương trình bậc nhất hai ẩn

\(\left\{{}\begin{matrix}\dfrac{2x}{x+1}+\dfrac{y}{y+1}=3\\\dfrac{x}{x+1}+\dfrac{3y}{y+1}=-1\end{matrix}\right.\)\(\left(Đk:x,y\ne-1\right)\)

\(\left\{{}\begin{matrix}\dfrac{2x}{x+1}+\dfrac{y}{y+1}=3\\\dfrac{2x}{x+1}+\dfrac{6y}{y+1}=-2\end{matrix}\right.\)

\(\Rightarrow\dfrac{5y}{y+1}=-5\)

\(\Leftrightarrow5y=-5y-5\)

\(\Leftrightarrow10y=-5\)

\(\Leftrightarrow y=-\dfrac{1}{2}\Rightarrow x=-2\)

<=>\(\dfrac{2x}{x+1}-\dfrac{x}{x+1}=4< =>x-4x=4< =>x=-\dfrac{4}{3}\Rightarrow y=-\dfrac{1}{4}\)

Đặt \(\sqrt{x+3}=a\); \(\sqrt{y+1}=b\) (a,b \(\ge0\))

\(\Rightarrow\left\{{}\begin{matrix}a-2b=2\\2a+b=4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2a-4b=4\\2a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5b=0\\2a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=2\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\sqrt{x+3}=2\\\sqrt{y+1}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)(tmđk)

Vậy hệ pt có nghiệm suy nhất (x;y) = (1;-1)

a: Khi m=2 thì hệ phương trình sẽ trở thành:

\(\left\{{}\begin{matrix}2x+3y=-4\\x-2y=5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x+3y=-4\\2x-4y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7y=-14\\x-2y=5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=-2\\x=2y+5=-4+5=1\end{matrix}\right.\)

b: Để hệ phương trình không có nghiệm thì \(\dfrac{m}{1}=\dfrac{3}{-2}< >-\dfrac{4}{5}\)

=>\(\dfrac{m}{1}=\dfrac{3}{-2}\)

=>\(m=\dfrac{3}{-2}=-\dfrac{3}{2}\)

cậu bổ sung đề vào nha

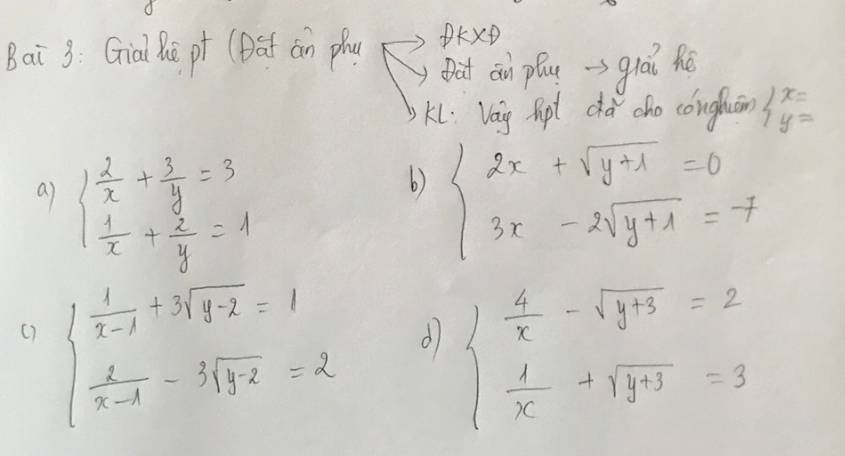
b: ĐKXĐ: y>=-1

Đặt \(\left\{{}\begin{matrix}x=a\\\sqrt{y+1}=b\left(b>=0\right)\end{matrix}\right.\)

Hệ phương trình sẽ trở thành:

2a+b=0 và 3a-2b=-7

=>4a+2b=0 và 3a-2b=-7

=>a=-1 và b=2

=>x=-1 và y+1=4

=>x=-1 và y=3

c: ĐKXĐ: x<>1 và y>=2

\(\left\{{}\begin{matrix}\dfrac{1}{x-1}=a\\\sqrt{y-2}=b\left(b>=0\right)\end{matrix}\right.\)

Hệ phương trình sẽ trở thành:

a+3b=1 và 2a-3b=2

=>3a=3 và a+3b=1

=>a=1 và b=0

=>x-1=1 và y-2=0

=>x=2 và y=2

d: ĐKXĐ: x<>0 và y>=-3

Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=a\\\sqrt{y+3}=b\left(b>=0\right)\end{matrix}\right.\)

Hệ phương trình sẽ trở thành:

4a-b=2 và a+b=3

=>5a=5 và a+b=3

=>a=1 và b=2

=>x=1 và y+3=4

=>x=1 và y=1

Ta bắt đầu bằng việc giả sử một giá trị ban đầu cho x, y và z, sau đó lặp lại quá trình tính toán cho đến khi đạt được độ chính xác mong muốn.

Ví dụ, giả sử ta chọn x = 1, y = 1 và z = 1 làm giá trị ban đầu. Sau đó, ta thực hiện các bước sau:

Bước 1: Tính toán giá trị mới cho x, y và z bằng cách sử dụng các phương trình đã cho: x_new = (2y - 1) / sqrt(y) y_new = (2z - 1) / sqrt(z) z_new = (2*x - 1) / sqrt(x)

Bước 2: Kiểm tra độ chính xác của giá trị mới so với giá trị cũ. Nếu đạt được độ chính xác mong muốn, ta dừng lại. Nếu không, ta lặp lại bước 1 với giá trị mới của x, y và z.

Tiếp tục lặp lại quá trình trên cho đến khi đạt được độ chính xác mong muốn. Khi đó, ta sẽ có giá trị x, y và z tương ứng là nghiệm của hệ phương trình đã cho.

Ta có: a+b+c=0\(\Leftrightarrow\)b+c=-a

Bình phương hai vế có: (b+c)²=a²

⇔ b²+2bc+c²=a²\(\Leftrightarrow\) b²+c²-a²=-2bc

Tương tự, ta có: c²+a²-b²=-2ca

                           a²+b²-c²=-2ab

→ A=\(-\dfrac{1}{2bc}-\dfrac{1}{2ca}-\dfrac{1}{2ab}=\dfrac{-\left(a+b+c\right)}{2abc}=0\)(vì a+b+c=0)

Vậy A=0

Δ=(-2)^2-4m=4-4m

Để phương trình có 2 nghiệm thì 4-4m>=0

=>4m<=4

=>m<=1

x1-x2=3

=>(x1-x2)^2=9

=>(x1+x2)^2-4x1x2=9

=>2^2-4m=9

=>4m=-5

=>m=-5/4(nhận)

k. ĐKXĐ: $x\geq \frac{2}{3}$

PT $\Leftrightarrow 4x^2-21x+22+\sqrt{3x-2}=0$

$\Leftrightarrow (4x^2-19x+18)-[(2x-4)-\sqrt{3x-2}]=0$

$\Leftrightarrow 4x^2-19x+18-\frac{(2x-4)^2-(3x-2)}{2x-4+\sqrt{3x-2}}=0$
$\Leftrightarrow (4x^2-19x+18)-\frac{4x^2-19x+18}{2x-4+\sqrt{3x-2}}=0$
$\Leftrightarrow (4x^2-19x+18)\left[1-\frac{1}{2x-4+\sqrt{3x-2}}\right]=0$
$\Rightarrow 4x^2-19x+18=0(1)$ hoặc $2x-4+\sqrt{3x-2}=0$

Với $(1)$ thì giải đơn giản rồi. 

Với $(2)$: 

$\Leftrightarrow \sqrt{3x-2}=4-2x$. Đến đây bình phương trình lên và giải như bình thường nhé.  

l.ĐKXĐ: ............

$(9x^2-32)+8(x-2\sqrt{8-2x^2})=0$

$\Leftrightarrow (9x^2-32)+8.\frac{x^2-4(8-2x^2)}{x+2\sqrt{8-2x^2}}=0$

$\Leftrightarrow (9x^2-32)+8.\frac{9x^2-32}{x+2\sqrt{8-2x^2}}=0$

$\Leftrightarrow (9x^2-32).\left[1+\frac{8}{x+2\sqrt{8-2x^2}}\right]=0$

TH1: $9x^2-32=0$

$\Leftrightarrow x=\frac{4\sqrt{2}}{3}$ (loại TH âm vì không thỏa mãn)

TH2: $1+\frac{8}{x+2\sqrt{8-2x^2}}=0$

$\Leftrightarrow x+2\sqrt{8-2x^2}=-8$

$\Leftrightarrow 2\sqrt{8-2x^2}=-8-x$

Với $8-2x^2\geq 0$ thì $-8-x<0$ nên pt này vô nghiệm 

Vậy $x=\frac{4\sqrt{2}}{3}$