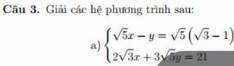\(\left\{{}\begin{matrix}\sqrt{5}x-y=\sqrt{5}\left(\sqrt{3}-1\right)\\2\sqrt{3}\cdot x+3\sqrt{5}y=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3\sqrt{5}\cdot x\sqrt{5}-3\sqrt{5}\cdot y=3\sqrt{5}\cdot\sqrt{5}\left(\sqrt{3}-1\right)\\2\sqrt{3}\cdot x+3\sqrt{5}y=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}15x-3\sqrt{5}\cdot y=15\left(\sqrt{3}-1\right)\\2\sqrt{3}\cdot x+3\sqrt{5}y=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(15+2\sqrt{3}\right)=15\sqrt{3}-15+21\\2\sqrt{3}\cdot x+3\sqrt{5}\cdot y=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{15\sqrt{3}+6}{15+2\sqrt{3}}=\sqrt{3}\\2\sqrt{3}\cdot x+3\sqrt{5}\cdot y=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\sqrt{3}\\y\cdot3\sqrt{5}+12=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\sqrt{3}\\y\cdot3\sqrt{5}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{3}\\y=\dfrac{3}{\sqrt{5}}=\dfrac{3\sqrt{5}}{5}\end{matrix}\right.\)
a) \(\left\{{}\begin{matrix}\sqrt{5}x-y=\sqrt{5}\left(\sqrt{3}-1\right)\\2\sqrt{3}x+3\sqrt{5}y=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{5}x-y=\sqrt{15}-\sqrt{5}\\2\sqrt{3}x+3\sqrt{5}y=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=\sqrt{3}-1\\2\sqrt{3}x+3\sqrt{5}y=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{3}x-2\sqrt{3}y=\sqrt{3}-1\\2\sqrt{3}x-3\sqrt{5}y=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2\sqrt{3}y=\sqrt{3}-22\\x-y=\sqrt{3}-1\end{matrix}\right.\left\{{}\begin{matrix}y=-24\\x-y=\sqrt{3}-1\end{matrix}\right.\left\{{}\begin{matrix}y=-24\\x+24=\sqrt{3}-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-24\\x=\sqrt{3}-25\end{matrix}\right.\left\{{}\begin{matrix}y=-24\\x=\sqrt{3}-\sqrt{\text{6}25}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-24\\x=-\sqrt{\text{6}22}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-24\\x\approx-25\end{matrix}\right.\left\{{}\begin{matrix}x\approx-25\\y=-24\end{matrix}\right.\)