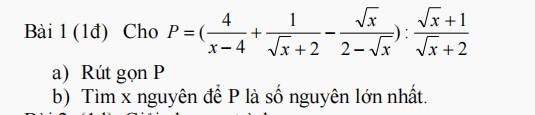Chương II - Hàm số bậc nhất

Hệ số góc của y=mx+2024 là m

Hệ số góc của y=(m+1)x+2025 là m+1

Theo đề, ta có: \(m^2+\left(m+1\right)^2=5\)

=>\(2m^2+2m+1-5=0\)

=>\(2m^2+2m-4=0\)

=>\(m^2+m-2=0\)

=>(m+2)(m-1)=0

=>\(\left[{}\begin{matrix}m=-2\\m=1\end{matrix}\right.\)

=>S có 2 phần tử

\(\left(d_1\right)y=mx+2m+1;\left(d_2\right)y=\left(2m-3\right)x-5\)

Để (d1) và (d2) cắt nhau thì:

\(m\ne2m-3\)

\(\Leftrightarrow2m-m\ne3\)

\(\Leftrightarrow m\ne3\) 

Để (d1) cắt (d2) thì \(2m-3\ne m\)

=>\(m\ne3\)

a) Đường thẳng `y=ax+2` song song với `y=-3x+1` nên ta có:

`=>a=-3` 

b) Đường thẳng `y=ax+2` cắt `y=2x+1` tại điểm có hoành độ bằng 2 

Ta có phương trình hoành độ giao điểm 

`ax+2=2x+1`

`<=>ax-2x=1-2`

`<=>x(a-2)=-1`

Thay `x=2` vào ta có:  

`2(a-2)=-1<=>a-2=-1/2<=>a=3/2` 

a: (d)//y=-3x+1

=>\(\left\{{}\begin{matrix}a=-3\\2\ne1\left(đúng\right)\end{matrix}\right.\)

=>a=-3

b:

Để hai đường thẳng y=ax+2 và y=2x-1 cắt nhau thì \(a\ne2\)

Thay x=2 vào y=2x+1, ta được:

\(y=2\cdot2+1=5\)

Thay x=2 và y=5 vào y=ax+2, ta được:

\(a\cdot2+2=5\)

=>2a=3

=>\(a=\dfrac{3}{2}\left(nhận\right)\)

Đề hiển thị lỗi rồi. Bạn xem lại.

ĐKXĐ: \(x\ge0;x\ne4\)

\(P=\left(\dfrac{4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right).\left(\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\right)\)

\(=\left(\dfrac{4+\sqrt{x}-2+x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right).\left(\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\right)\)

\(=\dfrac{\left(x+3\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)

\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\dfrac{\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+1\right)}\)

\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)

b.

\(P=\dfrac{\sqrt{x}-2+4}{\sqrt{x}-2}=1+\dfrac{4}{\sqrt{x}-2}\)

P nguyên lớn nhất khi \(\sqrt{x}-2\) là số nguyên dương nhỏ nhất

\(\Leftrightarrow\sqrt{x}-2=1\Rightarrow\sqrt{x}=3\)

\(\Rightarrow x=9\)

a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{4\right\}\end{matrix}\right.\)

\(P=\left(\dfrac{4}{x-4}+\dfrac{1}{\sqrt{x}+2}-\dfrac{\sqrt{x}}{2-\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)

\(=\left(\dfrac{4}{\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}+2\right)}+\dfrac{1}{\sqrt{x}+2}+\dfrac{\sqrt{x}}{\sqrt{x}-2}\right)\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)

\(=\dfrac{4+\sqrt{x}-2+\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)

\(=\dfrac{\sqrt{x}+2+\left(\sqrt{x}+2\right)\cdot\sqrt{x}}{\sqrt{x}+2}\cdot\dfrac{1}{\sqrt{x}+1}\)

\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}=1\)

b: Với mọi x nguyên thỏa mãn \(\left\{{}\begin{matrix}x>=0\\x\ne4\end{matrix}\right.\) thì P luôn bằng 1

Với \(m=2\Rightarrow y=3x+3\)

a. 

Để A thuộc ĐTHS

\(\Rightarrow2k+1=3k+3\)

\(\Rightarrow k=-2\)

b.

Gọi A là giao điểm của ĐTHS với Ox \(\Rightarrow y_A=0\)

\(\Rightarrow3x_A+3=0\Rightarrow x_A=-1\)

\(\RightarrowĐTHS\) cắt Ox tại điểm có tọa độ \(\left(-1;0\right)\)

GỌi B là giao điểm của ĐTHS với Oy \(\Rightarrow x_B=0\)

\(\Rightarrow y_B=3.0+3\Rightarrow y_B=3\)

\(\Rightarrow\) ĐTHS cắt Oy tại điểm có tọa độ \(\left(0;3\right)\)

c.

Để ĐTHS song song với \(y=\left(2k-1\right)x+1\)

\(\Rightarrow\left\{{}\begin{matrix}2k-1=3\\1\ne3\end{matrix}\right.\) \(\Rightarrow k=2\)

d.

Để ĐTHS cắt \(y=\left(k-2\right)x-10\)

\(\Rightarrow k-2\ne3\)

\(\Rightarrow k\ne5\)

a: Thay x=2 và y=0 vào (d), ta được:

\(2\left(a-1\right)+2\cdot0=a\)

=>2a-2=a

=>a=2

b: Để (d)//2x-3y=1 thì \(\dfrac{a-1}{2}=\dfrac{2}{-3}\ne\dfrac{a}{1}\)

=>\(\left\{{}\begin{matrix}-3\left(a-1\right)=4\\1\left(a-1\right)\ne2a\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a-1=-\dfrac{4}{3}\\a-1-2a\ne0\end{matrix}\right.\)

=>\(a=-\dfrac{1}{3}\)

c: (d): (a-1)x+2y=a

=>x(a-1)=a-2y

=>\(x=\dfrac{a-2y}{a-1}\)

NGhiệm tổng quát là \(x=\dfrac{a-2y}{a-1}\)

Đề đâu bạn nhỉ?

Câu 1: 

Ta có: \(y=2x+4\) có \(b=4\ne0\Rightarrow\) giao điểm của \(y=2x+4\) và \(y=x+m-4\) nên\(A\left(x;y\right)\ne O\left(0;0\right)\) 

Phương trình hoành độ giao điểm:

\(2x+4=x+m-7\)

\(\Leftrightarrow2x-x=m-7-4\)

\(\Leftrightarrow x=m-11\)

Thay vào \(y=2x+4\) \(\Rightarrow y=2\left(m-11\right)+4=2m-22+4=2m-17\)

Mà tọa độ giao điểm của hai điểm này thuộc góc phần tư thứ II nên có: 

Tung độ: \(y>0\)

Hoành độ: \(x< 0\) 

\(\Leftrightarrow\left\{{}\begin{matrix}2m-17>0\\m-11< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2m>17\\m< 11\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{17}{2}\\m< 11\end{matrix}\right.\)

\(\Leftrightarrow\dfrac{17}{2}< m< 11\)

Vậy: ... 

Câu 2:

Nếu \(y=-4x-1\) đi qua điểm I vậy 3 đường thẳng (d1), (d2), (d3) sẽ đồng quy tại I 

Phương trình hoành độ giao điểm của (d1) và (d3) là: 

\(2x+5=\left(m+1\right)x+2m-1\)

\(\Leftrightarrow2x-\left(m+1\right)x=2m-1-5\)

\(\Leftrightarrow x\left(2-m-1\right)=2m-6\)

\(\Leftrightarrow x\left(1-m\right)=2m-6\)

\(\Leftrightarrow x=\dfrac{2m-6}{1-m}\left(m\ne1\right)\) 

Ta thay vào (d1) ta có: \(y=2\cdot\dfrac{2m-6}{1-m}+5=\dfrac{4m-12+5-5m}{1-m}=\dfrac{m+7}{m-1}\) 

Lấy giá trị của x và y thay vào (d2) ta có:

\(\dfrac{m+7}{m-1}=-4\cdot\dfrac{2m-6}{1-m}-1\)

\(\Leftrightarrow\dfrac{m+7}{m-1}=\dfrac{8m-24}{m-1}-1\)

\(\Leftrightarrow\dfrac{8m-24-m-7}{m-1}-1=0\)

\(\Leftrightarrow\dfrac{7m-31}{m-1}=1\) 

\(\Leftrightarrow7m-31=m-1\)

\(\Leftrightarrow6m=30\)

\(\Leftrightarrow m=5\left(tm\right)\)

a: Gọi chiều dài mảnh vườn là x(m)

(Điều kiện: x>0; x<34/2=17)

Nửa chu vi mảnh vườn là 34:2=17(m)

Chiều rộng mảnh vườn là 17-x(m)

Chiều dài mảnh vườn sau khi tăng thêm 3m là x+3(m)

Chiều rộng mảnh vườn sau khi tăng thêm 2m là 17-x+2=19-x(m)

Diện tích mảnh vườn tăng thêm 45m² nên ta có phương trình:

\(\left(x+3\right)\left(19-x\right)-x\left(17-x\right)=45\)

=>\(19x-x^2+57-3x-17x+x^2=45\)

=>-x+57=45

=>x=12(nhận)

vậy: Chiều dài mảnh vườn là 12m

Chiều rộng mảnh vườn là 17-12=5(m)

b: Gọi thời gian hoàn thành công việc khi làm một mình của người thứ nhất và người thứ hai lần lượt là x(ngày) và y(ngày)

(Điều kiện: x>0; y>0)

Trong 1 ngày, người thứ nhất làm được: \(\dfrac{1}{x}\)(công việc)

Trong 1 ngày, người thứ hai làm được \(\dfrac{1}{y}\left(côngviệc\right)\)

Trong 1 ngày, hai người làm được \(\dfrac{1}{12}\)(công việc)

Do đó, ta có hệ phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\left(1\right)\)

Trong 4 ngày, người thứ nhất làm được: \(4\cdot\dfrac{1}{x}=\dfrac{4}{x}\left(côngviệc\right)\)

Trong 4+10=14 ngày, người thứ hai làm được \(\dfrac{14}{y}\left(côngviệc\right)\)

Vì sau khi làm chung 4 ngày, người thứ nhất được điều đi làm việc khác, người thứ hai hoàn thành phần còn lại sau 10 ngày nên ta có: \(\dfrac{4}{x}+\dfrac{14}{y}=1\left(2\right)\)

Từ (1),(2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{4}{x}+\dfrac{14}{y}=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{4}{y}=\dfrac{1}{3}\\\dfrac{4}{x}+\dfrac{14}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{10}{y}=-\dfrac{2}{3}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=15\\\dfrac{1}{x}=\dfrac{1}{12}-\dfrac{1}{15}=\dfrac{1}{60}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=60\\y=15\end{matrix}\right.\left(nhận\right)\)

Vậy: Thời gian người thứ nhất hoàn thành công việc khi làm một mình là 60 ngày

Thời gian người thứ hai hoàn thành công việc khi làm một mình là 15 ngày