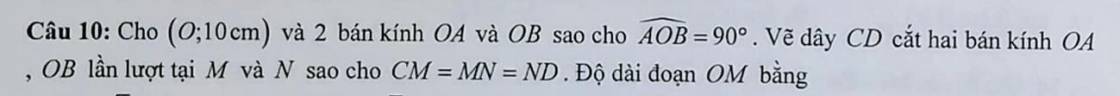và góc BOD = góc EIK . OKE
Chương II - Đường tròn
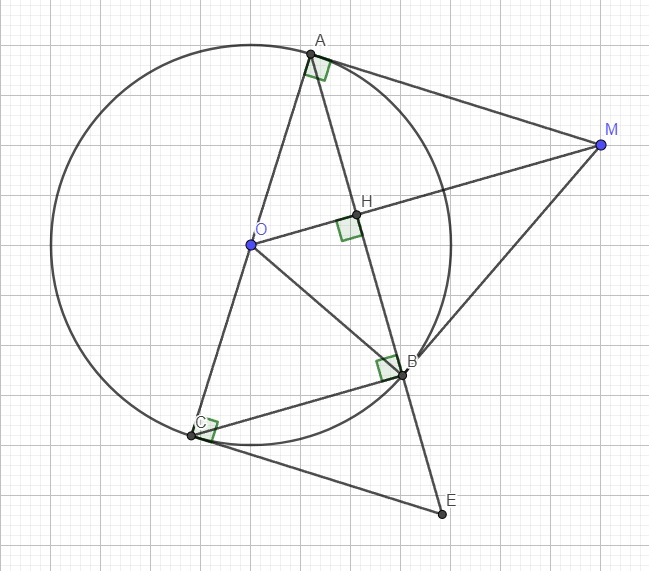
Từ điểm M bên ngoài đường tròn (O;R) vẽ hai tiếp tuyến MA,MB (A,B là các tiếp điểm). H là giao điểm của MO và AB. Kẻ đường kính BC của đường tròn (O;R). MC cắt đường tròn (O;R) tại điểm thứ hai là N (N khác C). Q là trung điểm của đoạn NC. 1) Cm: 4 điểm M,A,Q,O cùng nằm trên 1 đường tròn (CM theo 2 tam giác nội tiếp). ...
Đọc tiếp
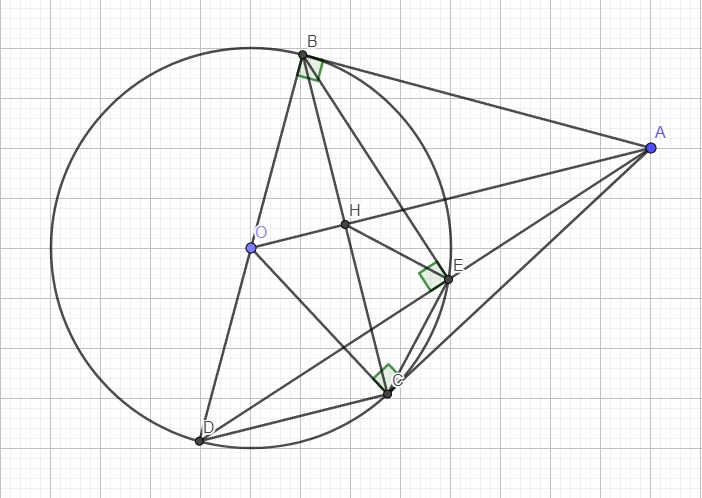
Từ điểm M bên ngoài đường tròn (O;R) vẽ hai tiếp tuyến MA,MB (A,B là các tiếp điểm). H là giao điểm của MO và AB. Kẻ đường kính BC của đường tròn (O;R). MC cắt đường tròn (O;R) tại điểm thứ hai là N (N khác C). Q là trung điểm của đoạn NC. 1) Cm: 4 điểm M,A,Q,O cùng nằm trên 1 đường tròn (CM theo 2 tam giác nội tiếp). 2) Cm: MA^2=MN.MC và góc MHN = góc MCO. 3) Gọi I là trung điểm của đoạn thẳng AC. Tiếp tuyến tại C của đường tròn (O;R) cắt tia BA tại D; tia DI cắt đoạn OC tại K; tia DO cắt đoạn AC ở E. Cm: \(\dfrac{AN}{AC}\)=\(\sqrt{\dfrac{MN}{MC}}\) và góc BOD = góc EIK
1: Ta có: ΔOCN cân tại O
mà OQ là đường trung tuyến
nên OQ\(\perp\)CN
Ta có: ΔOQM vuông tại Q
=>O,Q,M cùng thuộc đường tròn đường kính OM(1)
Ta có: ΔOAM vuông tại A
=>O,A,M cùng thuộc đường tròn đường kính OM(2)
Từ (1),(2) suy ra O,Q,M,A cùng thuộc một đường tròn
2: Xét (O) có
\(\widehat{MAN}\) là góc tạo bởi tiếp tuyến AM và dây cung AN
\(\widehat{NCA}\) là góc nội tiếp chắn cung NA
Do đó: \(\widehat{MAN}=\widehat{NCA}\)
Xét ΔMAN và ΔMCA có
\(\widehat{MAN}=\widehat{MCA}\)
\(\widehat{AMN}\) chung
Do đó: ΔMAN~ΔMCA
=>\(\dfrac{MA}{MC}=\dfrac{MN}{MA}\)
=>\(MA^2=MN\cdot MC\left(3\right)\)
Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(4)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(5)
Từ (4) và (5) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(6\right)\)
Từ (3),(6) suy ra \(MN\cdot MC=MH\cdot MO\)
=>\(\dfrac{MN}{MO}=\dfrac{MH}{MC}\)
Xét ΔMNH và ΔMOC có
\(\dfrac{MN}{MO}=\dfrac{MH}{MC}\)
\(\widehat{NMH}\) chung
Do đó: ΔMNH~ΔMOC
=>\(\widehat{MHN}=\widehat{MCO}\)
Đúng 2
Bình luận (1)
a: Ta có: \(\widehat{MHO}=90^0\)
=>H nằm trên đường tròn đường kính MO(1)
Ta có: \(\widehat{MAO}=\widehat{MBO}=90^0\)
=>M,A,B,O cùng thuộc đường tròn đường kính MO(2)
Từ (1) và (2) suy ra M,A,B,O,H cùng thuộc đường tròn đường kính MO
b: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(3)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(4)
Từ (3) và (4) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại I và I là trung điểm của AB
Xét ΔOIK vuông tại I và ΔOHM vuông tại H có
\(\widehat{IOK}\) chung
Do đó: ΔOIK~ΔOHM
=>\(\dfrac{OI}{OH}=\dfrac{OK}{OM}\)
=>\(OH\cdot OK=OI\cdot OM\)
Đúng 1
Bình luận (0)
Từ điểm M nằm ngoài (O), kẻ tiếp tuyến MA với (O), (A là tiếp điểm). Từ A kẻ đường thẳng vuông góc với OM tại H và cắt (O) tại B ( B khác A). Kẻ đường kính AC của (O). Tiếp tuyến tại C của (O) cắt đường thẳng AB tại E. a) CM: 4 điểm E,H,O,C cùng thuộc 1 đường tròn b) CM: Tam giác AMB cân c) CM: BE.BMBC.BO
Đọc tiếp
Từ điểm M nằm ngoài (O), kẻ tiếp tuyến MA với (O), (A là tiếp điểm). Từ A kẻ đường thẳng vuông góc với OM tại H và cắt (O) tại B ( B khác A). Kẻ đường kính AC của (O). Tiếp tuyến tại C của (O) cắt đường thẳng AB tại E. a) CM: 4 điểm E,H,O,C cùng thuộc 1 đường tròn b) CM: Tam giác AMB cân c) CM: BE.BM=BC.BO
a. Em tự giải
b.
\(\Delta OAB\) cân tại O (do \(OA=OB=R\), mà \(OH\) là đường vuông góc (do OH vuông góc AB)
\(\Rightarrow OH\) đồng thời là trung tuyến và trung trực của AB
Hay OM là trung trực của AB
\(\Rightarrow MA=MB\Rightarrow\Delta MAB\) cân tại M
c.
Do EC là tiếp tuyến tại C \(\Rightarrow EC\perp AC\)
MA là tiếp tuyến tại A \(\Rightarrow MA\perp AC\)
\(\Rightarrow EC||MA\Rightarrow\widehat{MAH}=\widehat{CEB}\) (so le trong)
Mà \(\widehat{MAH}=\widehat{MOA}\) (cùng phụ \(\widehat{AMH}\))
\(\Rightarrow\widehat{CEB}=\widehat{MOA}\)
Xét hai tam giác CEB và MOA có:
\(\left\{{}\begin{matrix}\widehat{CEB}=\widehat{MOA}\left(cmt\right)\\\widehat{CBE}=\widehat{MAO}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta CEB\sim\Delta MOA\left(g.g\right)\)
\(\Rightarrow\dfrac{BE}{OA}=\dfrac{BC}{AM}\Rightarrow BE.AM=BC.OA\)
Mà \(MA=MB\) (theo cm câu b) và \(OA=BO=R\)
\(\Rightarrow BE.BM=BC.BO\)
Đúng 2
Bình luận (1)
a: Xét tứ giác EHOC có \(\widehat{EHO}+\widehat{ECO}=90^0+90^0=180^0\)
nên EHOC là tứ giác nội tiếp
=>E,H,O,C cùng thuộc một đường tròn
b: Ta có: ΔOAB cân tại O
mà OH là đường cao
nên OH là phân giác của góc AOB
Xét ΔAOM và ΔBOM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔAOM=ΔBOM
=>MA=MB
=>ΔMAB cân tại M
c: Ta có: ΔAOM=ΔBOM
=>\(\widehat{OAM}=\widehat{OBM}=90^0\)
Xét tứ giác OAMB có \(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)
nên OAMB là tứ giác nội tiếp
=>\(\widehat{OMB}=\widehat{OAB}=\widehat{CAB}\left(1\right)\)
Xét (O) có
\(\widehat{CAB}\) là góc nội tiếp chắn cung CB
\(\widehat{ECB}\) là góc tạo bởi tiếp tuyến CE và dây cung CB
Do đó: \(\widehat{CAB}=\widehat{ECB}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{OMB}=\widehat{ECB}\)
Xét ΔOMB và ΔECB có
\(\widehat{OMB}=\widehat{ECB}\)
\(\widehat{OBM}=\widehat{EBC}=90^0\)
Do đó: ΔOMB~ΔECB
=>\(\dfrac{BO}{BE}=\dfrac{BM}{BC}\)
=>\(BO\cdot BC=BM\cdot BE\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
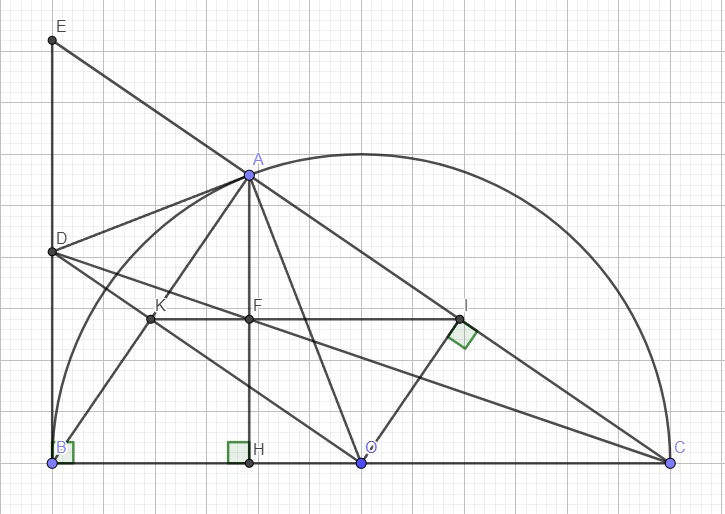
a.
BD là tiếp tuyến của (O) tại B \(\Rightarrow\widehat{OBD}=90^0\)
\(\Rightarrow\) 3 điểm O, B, D thuộc đường tròn đường kính OD (1)
AD là tiếp tuyến của (O) tại A \(\Rightarrow\widehat{OAD}=90^0\)
\(\Rightarrow\) 3 điểm O, A, D cùng thuộc đường tròn đường kính OD (2)
(1);(2)\(\Rightarrow\) 4 điểm A, D, B, O cùng thuộc 1 đường tròn
b.
Theo cmt ta có tam giác CBE vuông tại B và BA là đường cao ứng với cạnh huyền
Áp dụng hệ thức lượng:
\(CA.CE=CB^2\Rightarrow CA.CE=\left(2R\right)^2=4R^2\)
c.
D là giao điểm 2 tiếp tuyến tại A và B \(\Rightarrow AD=BD\)
Đồng thời \(OA=OB=R\)
\(\Rightarrow OD\) là trung trực của AB
\(\Rightarrow OD\perp AB\) tại K đồng thời K là trung điểm AB
Mà \(AB\perp AC\) (\(\widehat{BAC}\) là góc nt chắn nửa đường tròn)
\(\Rightarrow OK||AC\) hay \(OD||CE\)
Lại có O là trung điểm BC
\(\Rightarrow OD\) là đường trung bình tam giác BCE (đường thẳng đi qua 1 trung điểm và song song cạnh đáy)
\(\Rightarrow D\) là trung điểm BE \(\Rightarrow BD=DE\)
Trong tam giác ABH vuông tại H có KH là trung tuyến ứng với cạnh huyền \(\Rightarrow KH=\dfrac{1}{2}AB=AK\)
Trong tam giác ACH vuông tại H có IH là trung tuyến ứng với cạnh huyền \(\Rightarrow IH=\dfrac{1}{2}AC=AI\)
Xét 2 tam giác KAI và KHI có: \(\left\{{}\begin{matrix}AK=KH\\AI=IH\\IK\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta KAI=\Delta KHI\left(c.c.c\right)\)
\(\Rightarrow\widehat{KHI}=\widehat{KAC}=90^0\Rightarrow IH\perp KH\)
Mà tam giác ABH vuông tại H có K là trung điểm cạnh huyền \(\Rightarrow K\) là tâm đường tròn ngoại tiếp ABH hay KH là 1 bán kính
\(\Rightarrow IH\) là tiếp tuyến của đường tròn ngoại tiếp ABH
Do AH và BE cùng vuông góc AB \(\Rightarrow AH||BE\)
Gọi F là giao điểm của CD và AH
Áp đụng định lý Thales trong tam giác BCD: \(\dfrac{CF}{CD}=\dfrac{HF}{BD}\)
Áp dụng định lý Thales trong tam giác CDE: \(\dfrac{CF}{CD}=\dfrac{AF}{DE}\)
\(\Rightarrow\dfrac{HF}{BD}=\dfrac{AF}{DE}\Rightarrow HF=AF\) (do \(BD=DE\) theo cmt)
\(\Rightarrow F\) là trung điểm AH
OI vuông góc AC tại I \(\Rightarrow I\) là trung điểm AC
Trong tam giác ABC: K là trung điểm AB, I là trung điểm AC \(\Rightarrow KI\) là đường trung bình \(\Delta ABC\Rightarrow KI||BC\)
Trong tam giác ABH: K là trung điểm AB, F là trung điểm AH \(\Rightarrow KF\) là đường trung bình \(\Delta ABH\Rightarrow KF||BH\Rightarrow KF||BC\)
\(\Rightarrow I,K,F\) thẳng hàng hay KI đi qua F
\(\Rightarrow AH,KI,CD\) đồng quy tại F
Đúng 2
Bình luận (0)
Cho đường tròn (O;R) và một điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MB,MC tới (O) (B,C là tiếp điểm). Gọi H là giao điểm của MO với BC. Vẽ đường kính BA. a) Cm các điểm M,B,O,C cùng nằm trên 1 đg tròn b) Cm: CH^2OH.HM c) Gọi F là trung điểm của MH,AH cắt (O) tại giao điểm...
Đọc tiếp
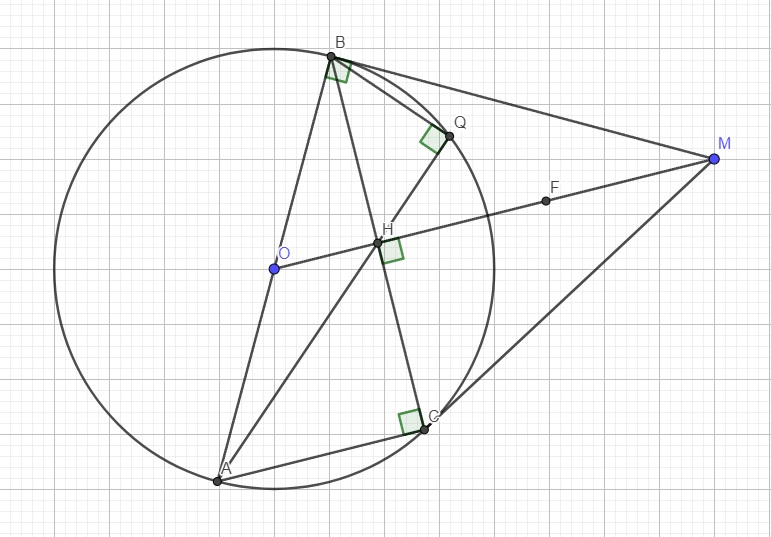
Cho đường tròn (O;R) và một điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MB,MC tới (O) (B,C là tiếp điểm). Gọi H là giao điểm của MO với BC. Vẽ đường kính BA. a) Cm các điểm M,B,O,C cùng nằm trên 1 đg tròn b) Cm: CH^2=OH.HM c) Gọi F là trung điểm của MH,AH cắt (O) tại giao điểm thứ hai là Q.Cm tam giác MBH đồng dạng tam giác BAC và B,Q,F thẳng hàng
a. Câu này đơn giản em tự giải.
b.
Ta có: \(\left\{{}\begin{matrix}OB=OC=R\\MB=MC\left(\text{t/c hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OM\) là trung trực của BC
\(\Rightarrow OM\perp BC\) tại H đồng thời H là trung điểm BC hay \(HB=HC\)
\(OC\perp MC\) (MC là tiếp tuyến tại C) \(\Rightarrow\Delta OMC\) vuông tại C
Áp dụng hệ thức lượng trong tam giác vuông OMC với đường cao CH:
\(CH^2=OH.MH\)
c.
C nằm trên đường tròn và AB là đường kính \(\Rightarrow\widehat{ACB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACB}=90^0\)
Xét hai tam giác MBH và BAC có:
\(\left\{{}\begin{matrix}\widehat{MHB}=\widehat{ACB}=90^0\\\widehat{MBH}=\widehat{BAC}\left(\text{cùng chắn BC}\right)\end{matrix}\right.\) \(\Rightarrow\Delta MBH\sim\Delta BAC\left(g.g\right)\)
\(\Rightarrow\dfrac{BH}{AC}=\dfrac{MH}{BC}\Rightarrow\dfrac{BH}{AC}=\dfrac{2HF}{2CH}\) (do F là trung điểm MH và H là trung điểm BC)
\(\Rightarrow\dfrac{BH}{AC}=\dfrac{HF}{CH}\)
Xét hai tam giác BHF và ACH có:
\(\left\{{}\begin{matrix}\dfrac{BH}{AC}=\dfrac{HF}{CH}\left(cmt\right)\\\widehat{BHF}=\widehat{ACH}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta BHF\sim\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{HBF}=\widehat{CAH}\)
Mà \(\widehat{CAH}=\widehat{CBQ}\) (cùng chắn CQ)
\(\Rightarrow\widehat{HBF}=\widehat{CBQ}\) hay \(\widehat{HBF}=\widehat{HBQ}\)
\(\Rightarrow B,Q,F\) thẳng hàng
Đúng 2
Bình luận (0)
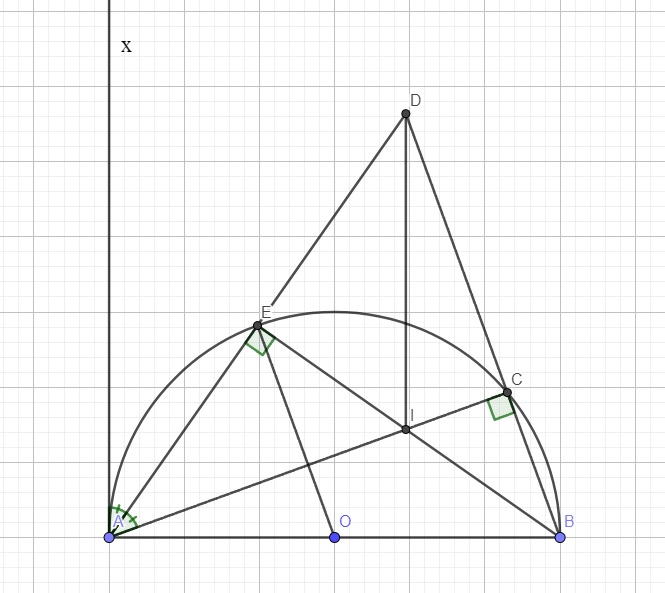
Bài 3: Cho nửa đường tròn (O) đường kính AB và AC là một dây của nó. Kẻ tiếp tuyến Ax và kẻ đường phân giác của góc CAx cắt nửa đường tròn tại E và cắt BC kéo dài tại D. a/C/m: AABD cân. b/ C/m: OE // BD. c/Gọi I là giao điểm của AC và BE. C/m: DI ⊥ AB. d/Tính độ dài AE, biết AB = 2cm và BAC = 20°,
a.
Do \(\widehat{ACB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ACB}=90^0\)
\(\Rightarrow\widehat{ACD}=90^0\Rightarrow\Delta ACD\) vuông tại C
\(\Rightarrow\widehat{ADC}+\widehat{DAC}=90^0\) (1)
Lại có \(\widehat{DAC}=\widehat{DAx}\) (do AD là phân giác)
\(\widehat{BAE}+\widehat{DAx}=90^0\) (Ax là tiếp tuyến tại A)
\(\Rightarrow\widehat{BAE}+\widehat{DAC}=90^0\) (2)
(1);(2) \(\Rightarrow\widehat{ADC}=\widehat{BAE}\)
\(\Rightarrow\Delta ABD\) cân tại B
b.
\(\widehat{AEB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{AEB}=90^0\Rightarrow AE\perp BE\)
\(\Rightarrow BE\) là đường cao trong tam giác BAD
Mà tam giác BAD cân tại B \(\Rightarrow BE\) đồng thời là trung tuyến
\(\Rightarrow E\) là trung điểm AD
Lại có O là trung điểm AB
\(\Rightarrow OE\) là đường trung bình tam giác ABD
\(\Rightarrow OE||BD\)
Đúng 1
Bình luận (0)
c.
Xét tam giác ABD có: \(AC\perp BD;BE\perp AD\)
\(\Rightarrow I\) là trực tâm tam giác ABD
\(\Rightarrow DI\) là đường cao thứ 3
\(\Rightarrow DI\perp AB\)
d.
Ta có: \(\widehat{BAC}+\widehat{CAx}=90^0\)
\(\Rightarrow\widehat{BAC}+2.\widehat{CAE}=90^0\)
\(\Rightarrow\widehat{CAE}=\dfrac{90^0-20^0}{2}=35^0\)
\(\Rightarrow\widehat{BAE}=\widehat{BAC}+\widehat{CAE}=20^0+35^0=55^0\)
Xét tam giác vuông ABE có:
\(cos\widehat{BAE}=\dfrac{AE}{AB}\Rightarrow AE=AB.cos\widehat{BAE}=2.cos55^0\approx1,15\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm Ở ,đt AB nằm trên cùng nửa mặt phẳng b chứa AB, kể TT AX với nửa ĐT tâm Ở qua M bất kì trên nửa ĐT kể TT với ĐT cắt AX tại c :1 CM ∆ACM cân; 2 CM bM //OC
1: Xét (O) có
CA,CM là các tiếp tuyến
Do đó: CA=CM
=>ΔCAM cân tại C
2: Ta có: CA=CM
=>C nằm trên đường trung trực của AM(1)
Ta có: OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra OC là đường trung trực của AM
=>OC\(\perp\)AM
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>AM\(\perp\)MB
mà AM\(\perp\)OC
nên OC//MB
Đúng 0
Bình luận (0)
Từ điểm A nằm ngoài đường tròn (O;R), vẽ 2 tiếp tuyến AB,AC với đường tròn (B,C là tiếp điểm). Gọi H là giao điểm của OA và BC. ( VẼ HÌNH HỘ MÌNH NHÉ) a) Cm: 4 điểm A,B,O,C cùng thuộc 1 đg tròn (CM theo 2 tam giác nội tiếp) b) Kẻ đg kính BD. Gọi E là giao điểm của đoạn thẳng AD với (O), E ko trùng với D. Cm: DE/BEBD/BA và tính góc HEC
Đọc tiếp
Từ điểm A nằm ngoài đường tròn (O;R), vẽ 2 tiếp tuyến AB,AC với đường tròn (B,C là tiếp điểm). Gọi H là giao điểm của OA và BC. ( VẼ HÌNH HỘ MÌNH NHÉ) a) Cm: 4 điểm A,B,O,C cùng thuộc 1 đg tròn (CM theo 2 tam giác nội tiếp) b) Kẻ đg kính BD. Gọi E là giao điểm của đoạn thẳng AD với (O), E ko trùng với D. Cm: DE/BE=BD/BA và tính góc HEC
a.
Do AB là tiếp tuyến của (O) \(\Rightarrow AB\perp OB\Rightarrow\Delta ABO\) vuông tại B
\(\Rightarrow\Delta ABO\) nội tiếp đường tròn đường kính OA (1)
Tương tự, do AC là tiếp tuyến của (O) \(\Rightarrow\Delta ACO\) vuông tại C
\(\Rightarrow\Delta ACO\) nội tiếp đường tròn đường kính OA (2)
(1);(2) \(\Rightarrow\)4 điểm A,B,O,C cùng thuộc đường tròn đường kính OA
b.
Do BD là đường kính và E là điểm thuộc đường tròn nên \(\widehat{BED}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{BED}=90^0\)
Xét hai tam giác EAB và EBD có:
\(\left\{{}\begin{matrix}\widehat{AEB}=\widehat{BED}=90^0\\\widehat{EBA}=\widehat{EDB}\left(\text{cùng phụ }\widehat{EBD}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta EAB\sim\Delta EBD\left(g.g\right)\Rightarrow\dfrac{DE}{BE}=\dfrac{BD}{AB}\)
//\(\widehat{BCD}\) là góc nội tiếp chắn nửa đường tròn \(\Rightarrow\widehat{BCD}=90^0\)
Do \(AB=AC\) (t/c hai tiếp tuyến cắt nhau) và \(OB=OC=R\)
\(\Rightarrow OA\) là trung trực của BC \(\Rightarrow OA\perp BC\) tại H
Xét hai tam giác BCD và AHB có:
\(\left\{{}\begin{matrix}\widehat{BCD}=\widehat{AHB}=90^0\\\widehat{ABC}=\widehat{BDC}\left(\text{cùng chắn cung BC}\right)\end{matrix}\right.\) \(\Rightarrow\Delta BCD\sim\Delta AHB\left(g.g\right)\)
\(\Rightarrow\dfrac{BD}{AB}=\dfrac{CD}{BH}\Rightarrow\dfrac{CD}{BH}=\dfrac{DE}{BE}\)
Xét hai tam giác CDE và BHE có:
\(\left\{{}\begin{matrix}\dfrac{CD}{BH}=\dfrac{DE}{BE}\\\widehat{CDE}=\widehat{HBE}\left(\text{cùng chắn }CE\right)\end{matrix}\right.\) \(\Rightarrow\Delta CDE\sim\Delta BHE\left(g.g\right)\)
\(\Rightarrow\widehat{CED}=\widehat{BEH}\)
Mà \(\widehat{BEH}+\widehat{DEH}=\widehat{BED}=90^0\)
\(\Rightarrow\widehat{HEC}=\widehat{CED}+\widehat{DEH}=90^0\)
Đúng 3
Bình luận (0)
a: Ta có: ΔOBA vuông tại B
=>B,O,A cùng nằm trên đường tròn đường kính OA(1)
Ta có: ΔOCA vuông tại C
=>O,C,A cùng nằm trên đường tròn đường kính OA(2)
Từ (1) và (2) suy ra B,O,A,C cùng thuộc một đường tròn
b: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>BE\(\perp\)ED tại E
=>BE\(\perp\)AD tại E
Xét ΔEBD vuông tại E và ΔEAB vuông tại E có
\(\widehat{EBD}=\widehat{EAB}\left(=90^0-\widehat{BDA}\right)\)
Do đó: ΔEBD~ΔEAB
=>\(\dfrac{ED}{EB}=\dfrac{BD}{AB}\)
Đúng 1
Bình luận (0)
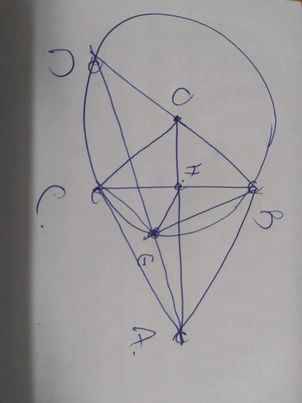
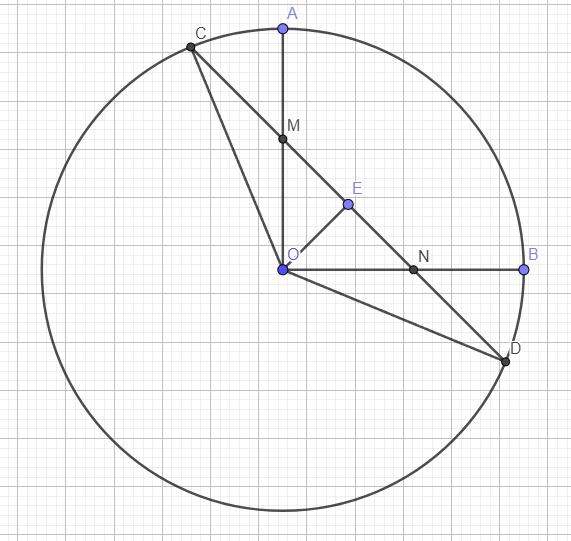
Gọi E là trung điểm MN \(\Rightarrow ME=NE\Rightarrow CE=DE\) (do \(CM=DN\))
\(\Rightarrow E\) là trung điểm CD \(\Rightarrow OE\perp CD\) tại E
\(\Rightarrow\Delta OMN\) cân tại O (do OE là trung tuyến đồng thời là đường cao)
Đặt \(EM=EN=a\Rightarrow CM=DN=2a\) đồng thời \(OE=\dfrac{1}{2}MN=ME=a\) (trung tuyến ứng với cạnh huyền)
Pitago tam giác OEC: \(OE^2+CE^2=OC^2\)
\(\Leftrightarrow a^2+\left(2a+a\right)^2=10^2\Rightarrow a=\sqrt{10}\)
Pitago tam giác OEM: \(a^2+a^2=OM^2\Rightarrow OM=a\sqrt{2}=\sqrt{20}=2\sqrt{5}\)
Đúng 2
Bình luận (0)