Chương 6: CUNG VÀ GÓC LƯỢNG GIÁC. CÔNG THỨC LƯỢNG GIÁC

Lời giải:

$A=2\cos ^3a+\cos ^2a-\sin ^2a+\sin a=2\cos ^3a+2\cos ^2a-1+\sin a$

$=2\cos ^2a(\cos a+1)-(1-\sin a)$

$=2(1-\sin ^2a)(\cos a+1)-(1-\sin a)$

$=2(1-\sin a)(1+\sin a)(\cos a+1)-(1-\sin a)$

$=(1-\sin a)[2(\sin a+1)(\cos a+1)-1]$

$=(1-\sin a)(2\sin a\cos a+2\sin a+2\cos a+1)$

$=(1-\sin a)(\sin 2a+2\sin a+2\cos a+1)$

\(A=sin^3x\cdot\left(1+\dfrac{cosx}{sinx}\right)+cos^3x\left(1+\dfrac{sinx}{cosx}\right)\)

\(=sin^2x\left(sinx+cosx\right)+cos^2x\left(cosx+sinx\right)\)
=cosx+sinx

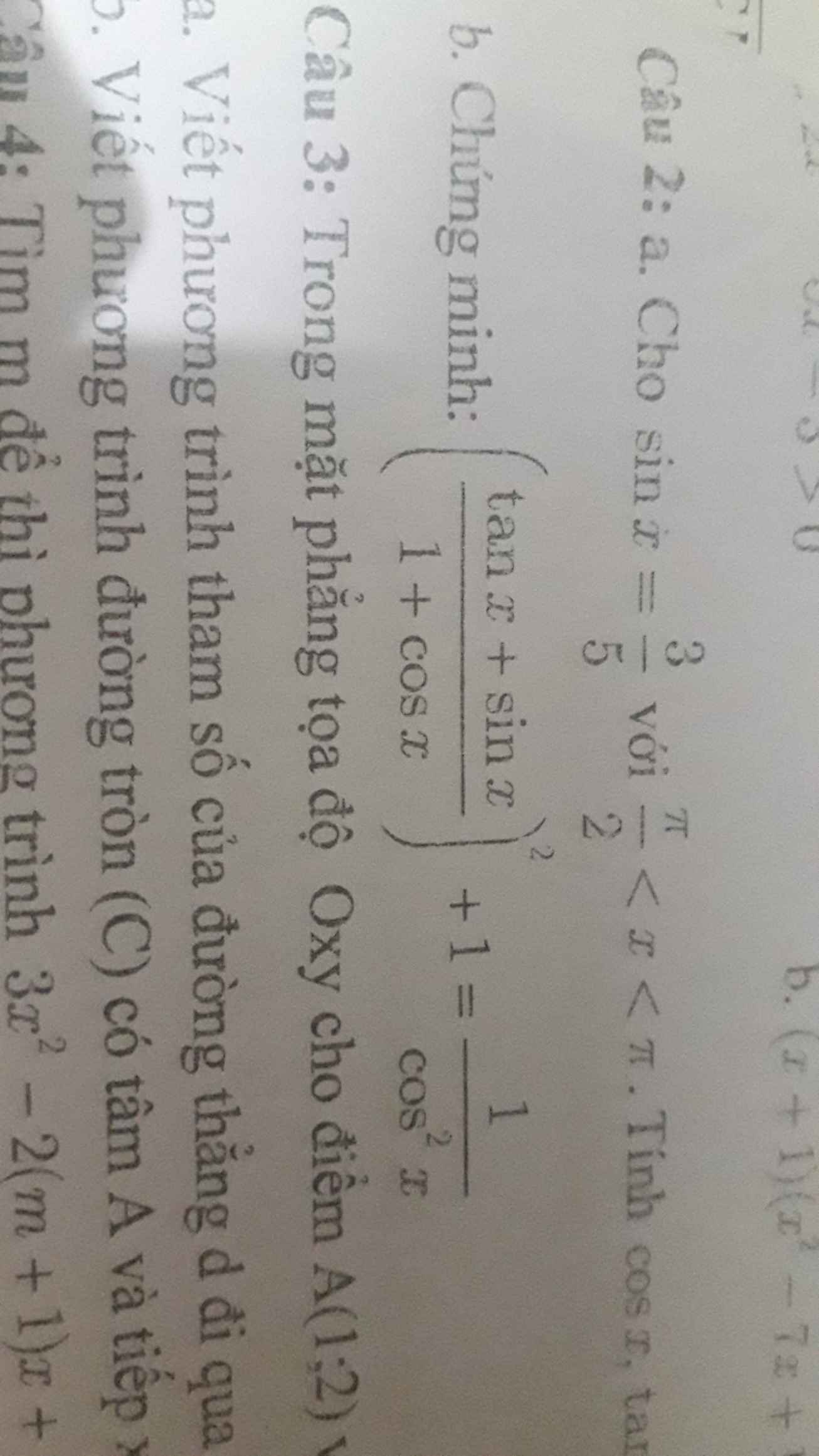
b: \(VT=\left[\dfrac{\dfrac{sinx}{cosx}+sinx}{1+cosx}\right]^2+1\)

\(=\left[\dfrac{sinx\left(\dfrac{1}{cosx}+1\right)}{cosx\left(1+\dfrac{1}{cosx}\right)}\right]^2+1\)

=1/cos^2x=VP

ai lm đc t gọi bằng cụ=))

tách ra ik:D
nhìn lóa mắt lun

`cot  x = -3 => cos x = -3 sin x`

`=> A = [ 2 sin^2 x + 3 sin x . (-3 sin x ) ] / [ sin^2 x - 7 ( sin^2 x + cos^2 x ) ]`

`<=>A = [ -7 sin^2 x ] / [ sin^2 x - 7 ( sin^2 x + 9 sin^2 x ) ]`

`<=>A = [ -7 sin^2 x ] / [ -69 sin^2 x ]`

`<=> A = 7 / 69`

pi/2<a,b<pi

=>cos a<0; cos b<0; sin a>0; sin b>0

\(cosa=-\sqrt{1-\left(\dfrac{3}{5}\right)^2}=-\dfrac{4}{5};sina=\sqrt{1-\left(-\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)

tan a=-3/5:4/5=-3/4; tan b=12/13:(-5/13)=-12/5

\(tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana\cdot tanb}\)

\(=\dfrac{-\dfrac{3}{4}+\dfrac{-12}{5}}{1-\dfrac{-3}{4}\cdot\dfrac{-12}{5}}=\dfrac{63}{16}\)

sin(a-b)=sina*cosb-sinb*cosa

\(=\dfrac{3}{5}\cdot\dfrac{-5}{13}-\dfrac{-4}{5}\cdot\dfrac{12}{13}=\dfrac{-15+48}{65}=\dfrac{33}{65}\)

\(E=\dfrac{\left(cosx-siny\right)\left(cosx+siny\right)}{sin^2x\cdot sin^2y}-\dfrac{cos^2x}{sin^2x}\cdot\dfrac{cos^2y}{sin^2y}\)

\(=\dfrac{cos^2x\left(1-cos^2y\right)-sin^2y}{sin^2x\cdot sin^2y}\)

\(=\dfrac{sin^2y\left(cos^2x-1\right)}{sin^2x\cdot sin^2y}=-1\)

b: tan^2a-sin^2a

\(=\dfrac{sin^2a}{cos^2a}-sin^2a\)

\(=sin^2a\left(\dfrac{1}{cos^2a}-1\right)\)

\(=sin^2a\cdot\dfrac{1-cos^2a}{cos^2a}=\dfrac{sin^2a}{cos^2a}\cdot sin^2a=sin^2a\cdot tan^2a\)

c: 1+sina+cosa+tan a

\(=1+cosa+sina\left(1+\dfrac{1}{cosa}\right)\)

\(=\left(1+cosa\right)\left(1+\dfrac{sina}{cosa}\right)\)

\(=\left(1+cosa\right)\left(1+tana\right)\)

\(d=\dfrac{\left(cos^4\left(x\right)-tanx\right)}{cos\left(2x\right)}:t=\dfrac{dcos\left(2x\right)-cos^4\left(x\right)}{anx};cos\left(2x\right)\ne0,n\ne0\)

\(\left\{{}\begin{matrix}d=\dfrac{\left(cos^4\left(x\right)-tanx\right)}{cos\left(2x\right)}\\\dfrac{cos^4\left(x\right)-tanx}{cos\left(2x\right)}=d\end{matrix}\right.\)  

\(\Leftrightarrow\) \(\dfrac{\left(cos^4\left(x\right)-tanx\right)cos\left(2x\right)}{cos\left(2x\right)}=dcos\left(2x\right);cos\left(2x\right)\ne0\)

\(\Leftrightarrow\) \(cos^4\left(x\right)-antx=dcos\left(2x\right);cos\left(2x\right)\ne0\)

\(\Leftrightarrow\) \(cos^4\left(x\right)-antx-cos^4\left(x\right)=dcos\left(2x\right)-cos^4\left(x\right);cos\left(2x\right)\ne0\)

\(\Leftrightarrow\) \(-antx=dcos\left(2x\right)-cos^4\left(x\right);cos\left(2x\right)\ne0\)

\(\Leftrightarrow\) \(\dfrac{-antx}{-anx}=\dfrac{dcos\left(2x\right)}{-anx}-\dfrac{cos^4\left(x\right)}{-anx};cos\left(2x\right)\ne0,n\ne0\)

\(\Rightarrow\) \(suy\) \(ra\) \(:\) \(d=-\dfrac{dcos\left(2x\right)-cos^4\left(x\right)}{-anx};cos\left(2x\right)\ne0,n\ne0\)