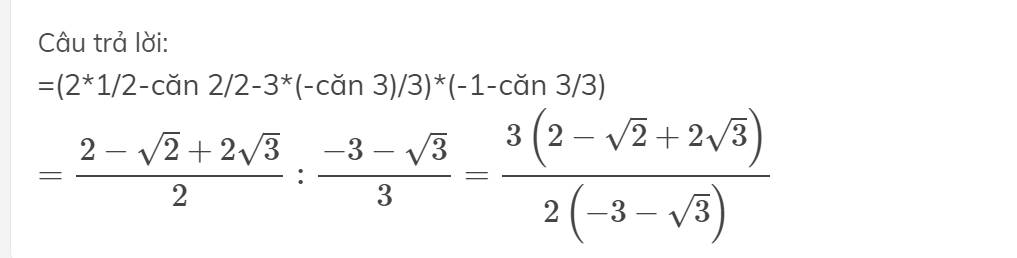Cho tam giác abc có bc=a ca=b ab=c (b khác c) diện tích s biết b^2+c^2>=2a^2 1) chứng minh 4S/(tanA)>=a^2 2) gọi o g lần lượt là tâm đg tròn ngoại tiếp và trọng tâm tam giác abc M là trung điểm bc chứng minh góc MGO không nhọn
Chương 6: CUNG VÀ GÓC LƯỢNG GIÁC. CÔNG THỨC LƯỢNG GIÁC
Trong mặt phẳng tọa độ Oxy, cho ba điểm A B 2; 4 , 1;0 và C2;2 . a) Tìm tọa độ điểm D sao cho ABCD là hình bình hành. b) Tìm tọa độ điểm M sao cho AM AB BC 2 . c) Tìm tọa độ điểm N đối xứng với điểm B qua điểm C. d) Tìm tọa độ điểm P nằm trên trục hoành sao cho A C P , , thẳng hàng.
a: A(2;4); B(1;0); C(2;2)
vecto AB=(-1;-4)
vecto DC=(2-x;2-y)
Vì ABCD là hình bình hành nên vecto AB=vecto DC
=>2-x=-1 và 2-y=-4
=>x=3 và y=6
c: N đối xứng B qua C
=>x+1=4 và y+0=4
=>x=3 và y=4
Đúng 0
Bình luận (0)
a: A(2;4); B(1;0); C(2;2)
vecto AB=(-1;-4)
vecto DC=(2-x;2-y)
Vì ABCD là hình bình hành nên vecto AB=vecto DC
đây nhé bạn
=>2-x=-1 và 2-y=-4
=>x=3 và y=6
c: N đối xứng B qua C
=>x+1=4 và y+0=4
=>x=3 và y=4
Đúng 0
Bình luận (0)
Cho tam giác ABC. Chứng minh cos(A + B)+ sin(A + B)= sinC - cosC
cos(A+B)+sin(A+B)
=cos(180-C)+sin(180-C)
=-cosC+sinC
Đúng 0
Bình luận (0)
H24
1 tháng 10 2022 lúc 20:25
Help mk đi mà...
Đọc tiếp
Help mk đi mà...
=(2*1/2-căn 2/2-3*(-căn 3)/3)*(-1-căn 3/3)
\(=\dfrac{2-\sqrt{2}+2\sqrt{3}}{2}:\dfrac{-3-\sqrt{3}}{3}=\dfrac{3\left(2-\sqrt{2}+2\sqrt{3}\right)}{2\left(-3-\sqrt{3}\right)}\)
Đúng 0
Bình luận (0)
H24
1 tháng 10 2022 lúc 20:22
Tính (ko dùng máy tính)
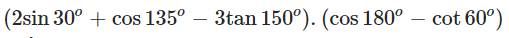
cho △ABC có AB=4, AC=8, BC=5. Tính S; R; r; cosC
\(p=\dfrac{a+b+c}{2}=\dfrac{17}{2}\)
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\dfrac{3\sqrt{119}}{4}\)
\(S=\dfrac{abc}{4R}\Rightarrow R=\dfrac{abc}{4S}=\dfrac{160}{3\sqrt{119}}\)
\(cosC=\dfrac{a^2+b^2-c^2}{2ab}=\dfrac{73}{80}\)
Đúng 0
Bình luận (0)
tìm a,b,c,góc A,góc B,góc C,r,R,S tam giác
tìm a,b,c,góc A,góc B,góc C,r,R,S tam giác
tìm a,b,c,góc A,góc B,góc C,r,R,S tam giác.giúp e vs ạ😭
tìm a,b,c,góc A,góc B,góc C,r,R,S tam giác
giúp e vs ạ🥹
giúp e với mng,e cần gấp🥹