Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức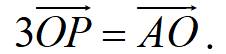
(1.0 điểm). Chứng minh đẳng thức .
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức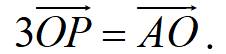
(1.0 điểm). Chứng minh đẳng thức .
\(3\overrightarrow{AP}-2\overrightarrow{AC}=\overrightarrow{0}\)
\(VT=3\left(\overrightarrow{AD}+\overrightarrow{DP}\right)-2\left(\overrightarrow{AD}+\overrightarrow{DC}\right)\)
\(=3\overrightarrow{AD}+3\overrightarrow{DP}-2\overrightarrow{AD}-2\overrightarrow{DC}\)
\(=\overrightarrow{AD}+3\overrightarrow{DP}-2\overrightarrow{DC}\)
\(=\overrightarrow{AD}+3\left(\overrightarrow{DC}+\overrightarrow{CP}\right)-2\overrightarrow{DC}\)
\(=\overrightarrow{AD}+3\overrightarrow{DC}+3\overrightarrow{CP}-2\overrightarrow{DC}\)
\(=\widehat{AD}+\overrightarrow{DC}+3.\dfrac{2}{3}\overrightarrow{CO}\)
\(=\overrightarrow{AD}+\overrightarrow{DC}+2.\dfrac{1}{2}\overrightarrow{CA}\)
\(=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CA}\)
\(=\overrightarrow{AC}+\overrightarrow{CA}\)
\(=\overrightarrow{AA}=\overrightarrow{0}=VP\) (điều phải chứng minh)
Cho hình vuông ABCD cạnh a.Tính các tích vô hướng sau: a)AB.AD;AB.BD b)(AB+AD).(BD+BC)
a: \(\overrightarrow{AB}\cdot\overrightarrow{AD}=0\)
\(\overrightarrow{AB}\cdot\overrightarrow{BD}=\overrightarrow{AB}\left(\overrightarrow{AD}-\overrightarrow{AB}\right)=-AB^2=-a^2\)
b: \(=\overrightarrow{AB}\cdot\overrightarrow{BD}+\overrightarrow{AB}\cdot\overrightarrow{BC}+\overrightarrow{AD}\cdot\overrightarrow{BD}+\overrightarrow{AD}\cdot\overrightarrow{BC}\)
\(=-a^2-\overrightarrow{BA}\cdot\overrightarrow{BC}+\overrightarrow{DA}\cdot\overrightarrow{DB}+AD^2\)
\(=-0+DA\cdot DB\cdot cos45=a\cdot a\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}=a^2\)
Cho tam giác ABC đều,cạnh bằng a,đường cao AH.Tính các tích vô hướng sau: a) BA.BC b)HB.BA
a: \(\overrightarrow{BA}\cdot\overrightarrow{BC}=BA\cdot BC\cdot cos60=\dfrac{1}{2}a^2\)
b: \(\overrightarrow{HB}\cdot\overrightarrow{BA}=\overrightarrow{HB}\left(\overrightarrow{HA}-\overrightarrow{HB}\right)=\overrightarrow{HB}\cdot\overrightarrow{HA}-HB^2=-HB^2=-\dfrac{1}{4}a^2\)
38.
Gọi I là trung điểm AB và G là trọng tâm tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\\\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\end{matrix}\right.\)
\(3\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=2\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(\Leftrightarrow3.\left|2\overrightarrow{MI}\right|=3\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=2.\left|3\overrightarrow{MG}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=6\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MI}\right|=\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow MI=MG\)
\(\Rightarrow\) Tập hợp M là đường trung trực của đoạn thẳng IG
\(\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}\left(\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AB}.\overrightarrow{CB}+\overrightarrow{AB}.\overrightarrow{BA}+\overrightarrow{AB}.\overrightarrow{AD}\)
\(=0-\overrightarrow{AB}^2+0=-4a^2\)
\(AH=\dfrac{1}{2}AC\Rightarrow AC=2AH=4a\)
\(\Rightarrow AB=AC=BC=4a\)
\(\overrightarrow{AB}.\overrightarrow{BC}=AB.BC.cos\left(\overrightarrow{AB};\overrightarrow{BC}\right)=4a.4a.cos120^0=-8a^2\)
\(\overrightarrow{AH}.\overrightarrow{CA}=-\overrightarrow{AH}.\overrightarrow{AC}=-AH.AC.cos\left(\overrightarrow{AH};\overrightarrow{AC}\right)=-2a.4a.cos0^0=-8a^2\)
Cần lắm người giải giúp
\(3\overrightarrow{MA}+2\overrightarrow{MB}=\overrightarrow{0}\) suy ra \(\dfrac{MB}{BA}=\dfrac{3}{5}\).
\(CPMQ\) là hình bình hành suy ra \(MP\) song song với \(CQ\), \(MQ\) song song với \(PC\).
Xét tam giác \(ABC\) có \(MP\) song song với \(BC\) suy ra \(\dfrac{AP}{AC}=\dfrac{AM}{AB}=\dfrac{2}{5}\).
Suy ra \(\overrightarrow{AP}=\dfrac{2}{5}\overrightarrow{AC}\).
Tương tự ta cũng suy ra được \(\overrightarrow{BQ}=\dfrac{3}{5}\overrightarrow{BC}\).
\(a\overrightarrow{NA}+b\overrightarrow{NQ}=\overrightarrow{0}\Leftrightarrow a\overrightarrow{AN}=b\overrightarrow{NQ}\) suy ra \(\overrightarrow{AQ}=\overrightarrow{AN}+\overrightarrow{NQ}=\overrightarrow{AN}+\dfrac{a}{b}\overrightarrow{AN}=\dfrac{a+b}{b}\overrightarrow{AN}\)
do đó \(\overrightarrow{AN}=\dfrac{b}{a+b}\overrightarrow{AQ}\).
Để \(B,N,P\) thẳng hàng thì \(\overrightarrow{BN}\) và \(\overrightarrow{BP}\) cùng phương. Ta sẽ phân tích \(\overrightarrow{BN},\overrightarrow{BP}\) theo hai vectơ \(\overrightarrow{BA}\) và \(\overrightarrow{BC}\).
\(\overrightarrow{BN}=\overrightarrow{BA}+\overrightarrow{AN}=\overrightarrow{BA}+\dfrac{b}{a+b}\overrightarrow{AQ}=\overrightarrow{BA}+\dfrac{b}{a+b}\left(\overrightarrow{AB}+\overrightarrow{BQ}\right)\)
\(=\overrightarrow{BA}-\dfrac{b}{a+b}\overrightarrow{BA}+\dfrac{3b}{5\left(a+b\right)}\overrightarrow{BC}=\dfrac{a}{a+b}\overrightarrow{BA}+\dfrac{3b}{5\left(a+b\right)}\overrightarrow{BC}\).
\(\overrightarrow{BP}=\overrightarrow{BA}+\overrightarrow{AP}=\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{AC}=\overrightarrow{BA}+\dfrac{2}{5}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)=\dfrac{3}{5}\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{BC}\).
\(\overrightarrow{BN},\overrightarrow{BP}\) cùng phương nên
\(\dfrac{\dfrac{a}{a+b}}{\dfrac{3}{5}}=\dfrac{\dfrac{3b}{5\left(a+b\right)}}{\dfrac{2}{5}}\Leftrightarrow\dfrac{2a}{5\left(a+b\right)}=\dfrac{9b}{25\left(a+b\right)}\Leftrightarrow10a=9b\).
Vì \(\left(a,b\right)=1\), \(a,b\) nguyên nên \(a=9,b=10\).
Vậy \(a+b=19\).
Cho tam giác \(ABC\) , \(M\) là điểm tùy ý trong mặt phẳng tam giác. Tìm giá trị nhỏ nhất biểu thức \(\left|2\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|+\left|\overrightarrow{MB}+\overrightarrow{MC}\right|\)?
Chỉ mik với ạ
Câu 2:
AB=BC=CD=DA=4a
\(AC=BD=\sqrt{2\cdot\left(4a\right)^2}=4a\sqrt{2}\)
\(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\widehat{BAC}\)
\(=4a\cdot4a\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}=16a^2\)
Vì AB vuông góc AD
nên vecto AB*vecto AD=0
vecto AB*vecto BC
=-vecto BC*vecto BA
=0
vecto AC*vecto CB
=-vecto CA*vecto CB
=-CA*CB*cos góc ACB
\(=-4a\sqrt{2}\cdot4a\cdot\dfrac{\sqrt{2}}{2}=-16a^2\)
vecto AD*vecto DC
=-vecto DA*vecto DC
=0