Chương 1: HÀM SỐ LƯỢNG GIÁC. PHƯƠNG TRÌNH LƯỢNG GIÁC

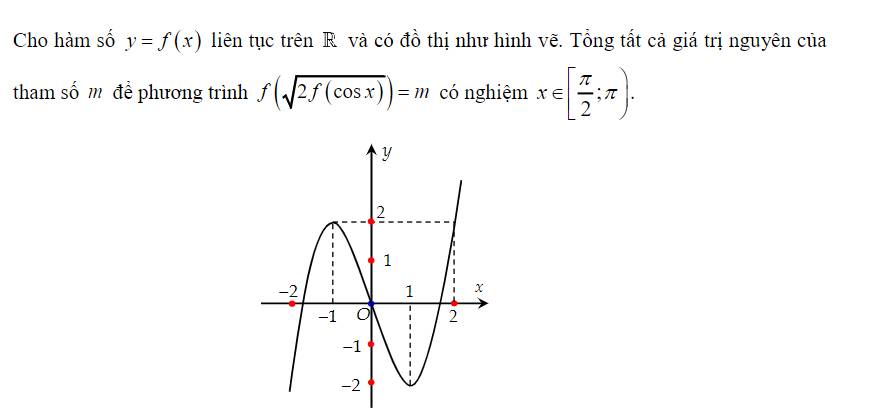
Khá đơn giản là làm dần từ trong ra ngoài:

\(x \in \left[\dfrac{\pi}{2};\pi \right) \Rightarrow cosx \in \left(-1;0\right]\Rightarrow \sqrt{2f(cosx)} \in (0;2]\)

Đặt \(\sqrt{2f\left(cosx\right)}=t\Rightarrow f\left(t\right)=m\) có nghiệm \(t\in(0;2]\)

\(\Rightarrow-2\le m\le2\)

Đề bài rất có vấn đề, chỉ có 3 giá trị nguyên dương của x thỏa mãn ĐKXĐ là 1;2;3. Như vậy chỉ cần thay lần lượt 3 giá trị này vào thử là xong, ko cần giải (ngay cả tự luận cũng được phép làm thế). Chắc ko ai cho đề kiểu vậy đâu.

Dạng này lâu quá quên cách làm rồi, thử vài cách xem cái nào tối ưu:

Sử dụng tam thức bậc 2:

Hàm xác định trên R khi:

\(2sin^2x-m.sinx+1>0;\forall x\in R\)

Đặt \(sinx=t\in\left[-1;1\right]\)

\(\Rightarrow f\left(t\right)=2t^2-m.t+1>0;\forall t\in\left[-1;1\right]\)

\(\Delta=m^2-8\)

TH1: \(\Delta< 0\Rightarrow-2\sqrt{2}< m< 2\sqrt{2}\)

Khi đó \(f\left(t\right)>0;\forall t\in R\)

TH2: \(\left\{{}\begin{matrix}\Delta=0\\-\dfrac{b}{2a}=\dfrac{m}{4}\notin\left[-1;1\right]\end{matrix}\right.\)  \(\Rightarrow\) ko có m thỏa mãn

TH3:  \(\left\{{}\begin{matrix}\Delta>0\\t_1< t_2< -1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m^2-8>0\\f\left(-1\right)=m+3>0\\\dfrac{t_1+t_2}{2}=\dfrac{m}{4}< -1\end{matrix}\right.\) \(\Rightarrow m\in\varnothing\)

TH4: \(\left\{{}\begin{matrix}\Delta>0\\1< t_1< t_2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m^2-8>0\\f\left(1\right)=3-m>0\\\dfrac{t_1+t_2}{2}=\dfrac{m}{4}>1\end{matrix}\right.\) \(\Rightarrow m\in\varnothing\)

Vậy \(-2\sqrt{2}< m< 2\sqrt{2}\)

- Sử dụng hẳng đẳng thức:

\(2sin^2x-m.sinx+1>0\)

\(\Leftrightarrow16sin^2x-8m.sinx+8>0\)

\(\Leftrightarrow\left(4sinx-m\right)^2-m^2+8>0\)

\(\Leftrightarrow\left(4sinx-m\right)^2>m^2-8\) (1)

TH1: \(m^2-8< 0\Rightarrow\) BPT luôn đúng

TH2: \(m^2-8\ge0\), khi đó (1) tương đương:

\(\left[{}\begin{matrix}4sinx-m>\sqrt{m^2-8}\\4sinx-m< -\sqrt{m^2-8}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}4sinx>m+\sqrt{m^2-8}\\4sinx< m-\sqrt{m^2-8}\end{matrix}\right.\)

Do \(sinx\in\left[-1;1\right]\) nên điều này đúng vói mọi x khi và chỉ khi:

\(\left[{}\begin{matrix}-4>m+\sqrt{m^2-8}\\4< m-\sqrt{m^2-8}\end{matrix}\right.\)  \(\Rightarrow\left[{}\begin{matrix}-1>\dfrac{m+\sqrt{m^2-8}}{4}\\1< \dfrac{m-\sqrt{m^2-8}}{4}\end{matrix}\right.\)(2)

Giải 2 cái này ra là được.

À, đến đây phát hiện ra 1 điều, thực chất \(\dfrac{m\pm\sqrt{m^2-8}}{4}\) chính là 2 nghiệm \(t_1;t_2\) của pt

\(2t^2-mt+1=0\), và 2 BPT (2) kia cũng chính là \(\left[{}\begin{matrix}t_1< t_2< -1\\1< t_1< t_2\end{matrix}\right.\) của cách 1

Vậy về cơ bản 2 cách này giống nhau về phần lõi, chỉ khác về cách trình bày

Sử dụng quy tắc cô lập m:

\(2sin^2x-m.sinx+1>0\Rightarrow2t^2-mt+1>0\) với \(t\in\left[-1;1\right]\)

- TH1: xét \(t\in\left(-1;0\right)\)

\(2t^2+1>mt\Rightarrow\dfrac{2t^2+1}{t}< m\) (do \(t< 0\) nên chia vế đảo dấu)

\(\Rightarrow m>\max\limits_{\left(-1;0\right)}\dfrac{2t^2+1}{t}\)

Có \(\dfrac{2t^2+1}{t}=2t+\dfrac{1}{t}=-\left(-2t+\left(-\dfrac{1}{t}\right)\right)\le-2\sqrt{\left(-2t\right).\left(-\dfrac{1}{t}\right)}=-2\sqrt{2}\)

\(\Rightarrow m>-2\sqrt{2}\)

TH2: xét \(t\in\left(0;1\right)\) (với t=0 hàm hiển nhiên xác định với mọi m)

\(2t^2+1>mt\Rightarrow\dfrac{2t^2+1}{t}>m\)

\(\Rightarrow m< \min\limits_{\left(0;1\right)}\dfrac{2t^2+1}{t}\)

Do \(\dfrac{2t^2+1}{t}=2t+\dfrac{1}{t}\ge2\sqrt{\dfrac{2t}{t}}=2\sqrt{2}\) (dấu = xảy ra với \(t\in\left(0;1\right)\) thỏa mãn)

\(\Rightarrow m< 2\sqrt{2}\)

Kết hợp: \(-2\sqrt{2}< m< 2\sqrt{2}\)

\(2sinx.sin3x+4m.sin2x-cos2x-m^2+1\ge0;\forall x\)

\(\Leftrightarrow-cos4x+4m.sin2x-m^2+1\ge0\)

\(\Leftrightarrow2sin^22x+4m.sin2x-m^2\ge0\)

\(\Leftrightarrow2t^2+4m.t-m^2\ge0\) ; \(\forall t\in\left[-1;1\right]\)

\(\Leftrightarrow\left(t+m\right)^2\ge\dfrac{3m^2}{2}\)

\(\Rightarrow\left[{}\begin{matrix}t+m\ge\sqrt{\dfrac{3m^2}{2}}\\t+m\le-\sqrt{\dfrac{3m^2}{2}}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}t\ge-m+\sqrt{\dfrac{3m^2}{2}}\\t\le-m-\sqrt{\dfrac{3m^2}{2}}\end{matrix}\right.\)

Điều này đúng với mọi \(t\in\left[-1;1\right]\) khi:

\(\left[{}\begin{matrix}-1\ge-m+\sqrt{\dfrac{3m^2}{2}}\left(1\right)\\1\le-m-\sqrt{\dfrac{3m^2}{2}}\left(2\right)\end{matrix}\right.\)

- Xét (1), nếu \(m\le0\Rightarrow-m\ge0\Rightarrow-m+\sqrt{\dfrac{3m^2}{2}}>0\) (ktm)

Với \(m>0\Rightarrow-1\ge-m+m\sqrt{\dfrac{3}{2}}\Rightarrow m\le-2-\sqrt{6}\)

- Xét (2), với \(m>0\Rightarrow-m-\sqrt{\dfrac{3m^2}{2}}< 0\) (ktm)

Với \(m< 0\Rightarrow1\le-m+m\sqrt{\dfrac{3}{2}}\Rightarrow m\ge2+\sqrt{6}\)

Vậy \(\left[{}\begin{matrix}m\le-2-\sqrt{6}\\m\ge2+\sqrt{6}\end{matrix}\right.\)

Cách tam thức có vẻ tốt hơn cách này

Cách tam thức:

\(f\left(t\right)=2t^2+4mt-m^2\ge0;\forall t\in\left[-1;1\right]\)

Với \(m=0\) luôn thỏa mãn

Với \(m\ne0:\)

\(\Delta'=4m^2+2m^2=6m^2>0\); \(\forall m\ne0\)

\(\Rightarrow\) Bài toán thỏa mãn khi: \(\left[{}\begin{matrix}1\le t_1< t_2\\t_1< t_2\le-1\end{matrix}\right.\)

TH1: \(1\le t_1< t_2\Rightarrow\left\{{}\begin{matrix}f\left(1\right)\ge0\\\dfrac{t_1+t_2}{2}=-m>1\\\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-m^2+4m+2\ge0\\m< -1\end{matrix}\right.\) \(\Rightarrow m\in\varnothing\)

A, đến đây mới thấy cách làm hồi nãy quên hợp lại, xét TH \(m>0\) ra nghiệm \(m\le-2-\sqrt{6}\) mà quên luôn điều kiện m>0

TH2: \(t_1< t_2\le-1\Rightarrow\left\{{}\begin{matrix}f\left(-1\right)\ge0\\\dfrac{t_1+t_2}{2}=-m< -1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-m^2-4m+2\ge0\\m>1\end{matrix}\right.\) \(\Rightarrow m\in\varnothing\)

Vậy \(m=0\) là giá trị duy nhất thỏa mãn

Phát hiện thêm 1 vấn đề nữa, \(A^2\ge B^2\Rightarrow\left[{}\begin{matrix}A\ge B\\A\le-B\end{matrix}\right.\) là sai, thực tế phức tạp và nhiều trường hợp hơn nhiều

Vậy thì chỉ có cách tam thức này là ổn thôi nếu ko cô lập được m. Kiểu bình phương kia sai mất căn bản.

Ủa sao xài hoành độ đỉnh ở đây được nhỉ, phải xài nghiệm (đúng hơn là lợi dụng quy tắc dấu tam thức bậc 2 "trong khác - ngoài cùng")

Đây, ví dụ 1 trường hợp cho em (bài này ở trên đã đưa dấu a>0 theo thói quen). 2 đường màu đỏ là khoảng \(\left(-1;\dfrac{1}{2}\right)\), rõ ràng đỉnh parabol nằm trong khoảng đó nhưng trên khoảng \(\left(-1;\dfrac{1}{2}\right)\) hàm vẫn có 1 đoạn nhận giá trị dương (tương ứng với đoạn BC)

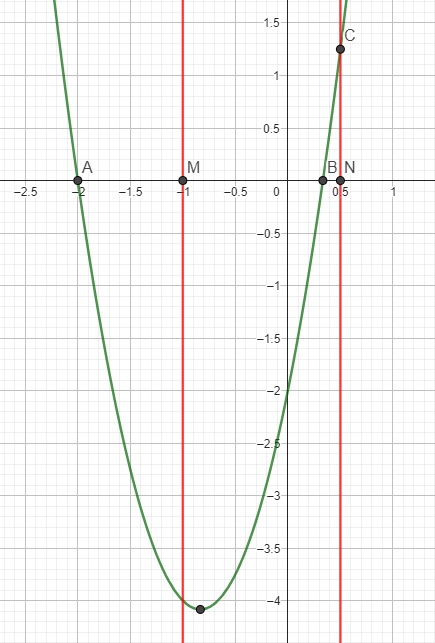
Cách làm đúng ở đây là cần sử dụng quy tắc tam thức bậc 2  (hoặc 1 số pp khác nhưng ko thể là hoành độ đỉnh). Lợi dụng quy tắc tam thức bậc 2: nếu pt bậc 2 có 2 nghiệm \(x_1;x_2\) thì \(a.f\left(x\right)< 0\) với \(x\in\left(x_1;x_2\right)\) và \(a.f\left(x\right)>0\) với \(x\notin\left(x_1;x_2\right)\).

Do đó để  \(f\left(x\right)< 0\) ; \(\forall x\in\left(p;q\right)\) nào đó (khi a dương), đồng nghĩa khi đó p và q phải nằm giữa 2 nghiệm, hay \(f\left(p\right)\) và \(f\left(q\right)\) đều âm.

Hàm xác định trên khoảng đã cho khi và chỉ khi:

\(4\left(sin^6x+cos^6x\right)-6m.sin2x+2-m^2\ge0;\forall x\in\left(...\right)\)

\(\Leftrightarrow4\left[\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\right]-6m.sin2x+2-m^2\ge0;\forall x\in...\)

\(\Leftrightarrow-3sin^22x-6m.sin2x-m^2+6\ge0\)

Đặt \(sin2x=t\Rightarrow t\in[-1;\dfrac{1}{2})\)

\(\Rightarrow f\left(t\right)=3t^2+6mt+m^2-6\le0\)

Theo định lý về dấu của tam thức bậc 2 thì điều này xảy ra khi và chỉ khi:

\(\left\{{}\begin{matrix}f\left(-1\right)\le0\\f\left(\dfrac{1}{2}\right)< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2-6m-3\le0\\m^2+3m-\dfrac{21}{4}< 0\end{matrix}\right.\)

Ủa biến đổi có sai ở đâu ko mà BPT cuối nhìn nghiệm xấu vậy

Hàm số xác định trên R khi và chỉ khi:

\(sin^2x+\left(2m-3\right)cosx+3m-2>0;\forall x\in R\)

\(\Leftrightarrow-cos^2x+\left(2m-3\right)cosx+3m-1>0\)

\(\Leftrightarrow t^2-\left(2m-3\right)t-3m+1< 0;\forall t\in\left[-1;1\right]\)

\(\Leftrightarrow t^2+3t+1< m\left(2t+3\right)\)

\(\Leftrightarrow\dfrac{t^2+3t+1}{2t+3}< m\) (do \(2t+3>0;\forall t\in\left[-1;1\right]\))

\(\Leftrightarrow m>\max\limits_{\left[-1;1\right]}\dfrac{t^2+3t+1}{2t+3}\)

Ta có: \(\dfrac{t^2+3t+1}{2t+3}=\dfrac{t^2+t-2+2t+3}{2t+3}=\dfrac{\left(t-1\right)\left(t+2\right)}{2t+3}+1\)

Do \(-1\le t\le1\Rightarrow\dfrac{\left(t-1\right)\left(t+2\right)}{2t+3}\le0\)

\(\Rightarrow\max\limits_{\left[-1;1\right]}\dfrac{t^2+3t+1}{2t+3}=1\)

\(\Rightarrow m>1\)

Hàm xác định trên R khi và chỉ khi:

\(sin^4x+cos^4x+4sinx.cosx+m-5\ge0;\forall m\)

\(\Leftrightarrow sin^4x+cos^4x+4sinx.cosx-5\ge-m;\forall m\)

\(\Leftrightarrow-m\le\min\limits_{x\in R}f\left(x\right)\)

Với \(f\left(x\right)=sin^4x+cos^4x+4sinx.cosx-5\)

Ta có:

\(f\left(x\right)=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x+4sinx.cosx-5\)

\(=-\dfrac{1}{2}\left(2sinx.cosx\right)^2+2sin2x-4\)

\(=-\dfrac{1}{2}sin^22x+2sin2x-4\)

\(=\dfrac{1}{2}\left(-sin^22x+4sin2x+5\right)-\dfrac{13}{2}\)

\(=\dfrac{1}{2}\left(5-sin2x\right)\left(sin2x+1\right)-\dfrac{13}{2}\ge-\dfrac{13}{2}\) do \(-1\le sin2x\le1\)

\(\Rightarrow\min\limits_{x\in R}f\left(x\right)=-\dfrac{13}{2}\Rightarrow m\ge\dfrac{13}{2}\)

Chắc là đề ko đúng đâu, vì cực trị (tức là điểm mà tại đó mà hàm đổi tính chất từ đồng biến sang nghịch biến) của bài này rất xấu, nó là giá trị x thỏa mãn \(sinx=\dfrac{3}{5}\). Với lượng giác thì đây là 1 giá trị cực xấu.

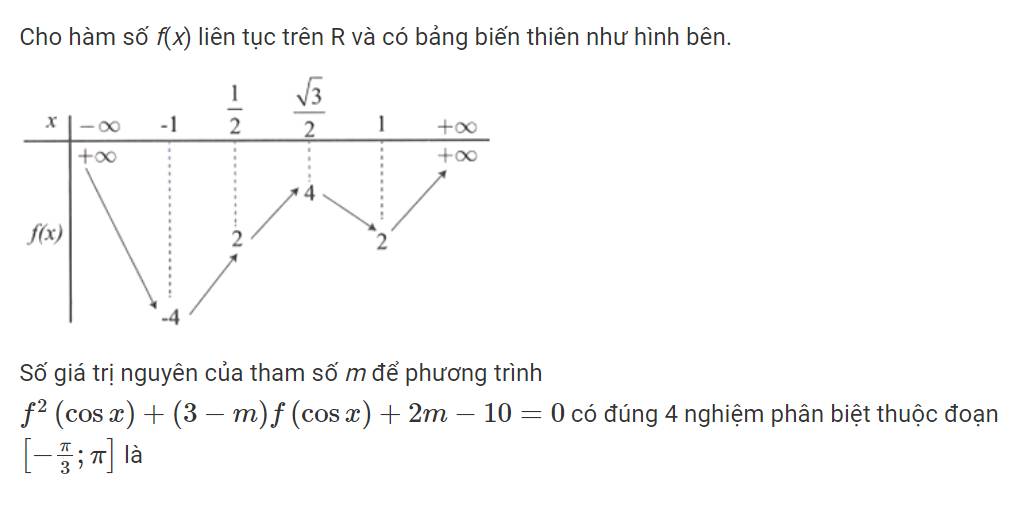
Đặt \(f\left(cosx\right)=t\)

\(\Rightarrow t^2+\left(3-m\right)t+2m-10=0\)

\(\Leftrightarrow t^2+3t-10-mt+2m=0\)

\(\Leftrightarrow\left(t-2\right)\left(t+5\right)-m\left(t-2\right)=0\)

\(\Leftrightarrow\left(t-2\right)\left(t-m+5\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}t=2\\t=m-5\end{matrix}\right.\)

Xét \(f\left(cosx\right)=2\) , từ đồ thị ta suy ra \(\left[{}\begin{matrix}cosx=1\\cosx=\dfrac{1}{2}\\cosx=k< -1\end{matrix}\right.\)

Pt có các nghiệm \(x=0;-\dfrac{\pi}{3};\dfrac{\pi}{3}\) (1) thuộc đoạn đã cho

\(\Rightarrow\) Bài toán thỏa mãn khi \(f\left(cosx\right)=m-5\) có 1 nghiệm thuộc đoạn đã cho

Từ đường tròn lượng giác \(\Rightarrow-1\le cosx< \dfrac{1}{2}\)

\(\Rightarrow\) Từ đồ thị \(\Rightarrow-4\le m-5< 2\Rightarrow1\le m< 7\)

Câu 1: D

Câu 3: A

Câu 4: C

Câu 5: D

Câu 6: C

Câu 7: A

Câu 8: A

Câu 9: C

Câu 10: A

Câu 11: B

Câu 12: C

Câu 13: A

Câu 2: A

Câu 14; C

Câu 15: A