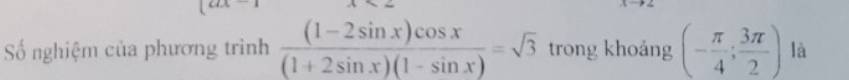
Chương 1: HÀM SỐ LƯỢNG GIÁC. PHƯƠNG TRÌNH LƯỢNG GIÁC
Cho tập hợp A = {0;1;2;3;4;5;6;7}. Từ tập A có thể lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau đôi một sao cho các số này lẻ
Gọi số cần lập có dạng \(\overline{abcde}\)
e có 4 cách chọn (từ 1;3;5;7)
a có 6 cách chọn (khác 0 và e)
b có 6 cách chọn (khác a và e)
c có 5 cách chọn (khác a,b,e)
d có 4 cách chọn (khác a,b,c,e)
Theo quy tắc nhân, có: \(4.6.6.5.4=...\) số
Đúng 3
Bình luận (0)
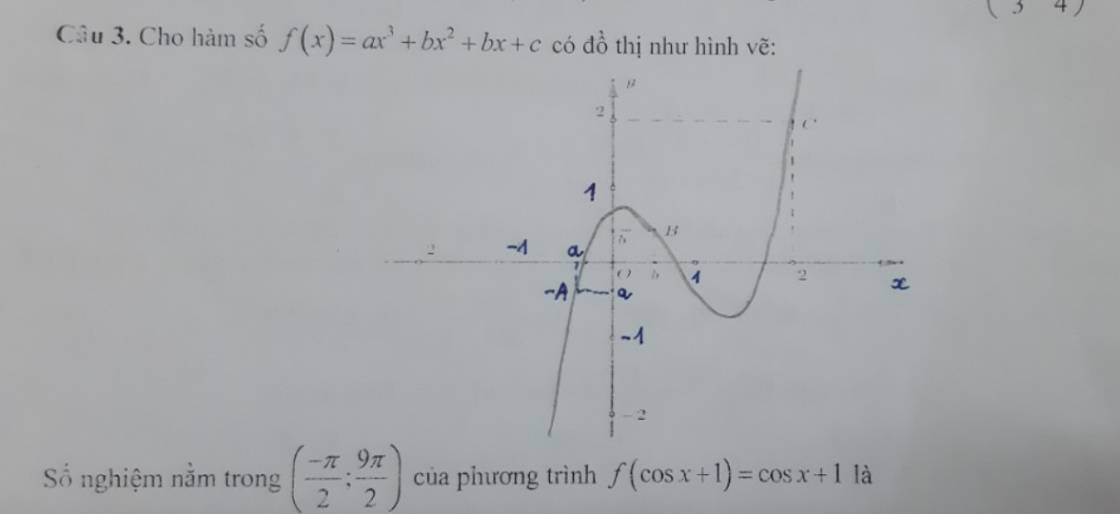
Vẽ đường thẳng \(y=x\) lên cùng hệ trục
\(\Rightarrow y=f\left(x\right)\) và \(y=x\) cắt nhau tại các điểm \(x=-1;x=1;x=2\)
Do đó \(f\left(cosx+1\right)=cosx+1\) có các nghiệm \(\left[{}\begin{matrix}cosx+1=-1\\cosx+1=1\\cosx+1=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}cosx=0\\cosx=1\end{matrix}\right.\) \(\Rightarrow...\)
Đúng 2
Bình luận (2)
Cho dãy số ($u_n$) biết \(u_{n+1}=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{\left(2n-1\right)\left(2n+1\right)}\) . Xác dịnh số hạng thứ 50 của dãy số
\(u_{n+1}=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{\left(2n-1\right)\cdot\left(2n+1\right)}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{\left(2n-1\right)\left(2n+1\right)}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2n-1}-\dfrac{1}{2n+1}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{2n+1}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2n+1-1}{2n+1}=\dfrac{n}{2n+1}\)
=>\(u_{50}=u_{49+1}=\dfrac{49}{2\cdot49+1}=\dfrac{49}{99}\)
Đúng 1
Bình luận (0)
\(y=\left|sin^4x-2sin^2x+1+m\right|=\left|\left(sin^2x-1\right)^2+m\right|\)
Do \(0\le\left(sin^2x-1\right)^2\le1\)
TH1: \(m\ge0\Rightarrow y=\left(sin^2x-1\right)^2+m\ge m\Rightarrow m=2\)
TH2: \(-1\le m\le0\Rightarrow\left(sin^2x-1\right)^2+m=0\) có nghiệm
\(\Rightarrow\left|\left(sin^2x-1\right)^2+m\right|\ge0\) (có xảy ra dấu =) nên \(y_{min}=0\) ko thỏa mãn
TH3: \(m< -1\Rightarrow\left(sin^2x-1\right)^2+m< 0;\forall x\)
\(\Rightarrow y=\left|\left(sin^2x-1\right)^2+m\right|=-\left(sin^2x-1\right)^2-m\ge-1-m\)
\(\Rightarrow-1-m=2\Rightarrow m=-3\)
B đúng
Đúng 2
Bình luận (2)
ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne-\dfrac{1}{2}\\sinx\ne1\end{matrix}\right.\)
\(\left(1-2sinx\right)cosx=\sqrt{3}\left(1+2sinx\right)\left(1-sinx\right)\)
\(\Leftrightarrow cosx-2sinx.cosx=\sqrt{3}+\sqrt{3}sinx-2\sqrt{3}sin^2x\)
\(\Leftrightarrow cosx-sin2x=\sqrt{3}+\sqrt{3}sinx-\sqrt{3}\left(1-cos2x\right)\)
\(\Leftrightarrow cosx-sin2x=\sqrt{3}sinx+\sqrt{3}cos2x\)
\(\Leftrightarrow cosx-\sqrt{3}sinx=sin2x+\sqrt{3}cos2x\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{1}{2}sin2x+\dfrac{\sqrt{3}}{2}cos2x\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=cos\left(2x-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow...\)
Đúng 2
Bình luận (0)
Tính tổng tất cả các nghiệm thuộc [0;2022\(\pi\)] của phương trình \(\dfrac{3-cos2x+sin2x-5sinx-cosx}{2cosx+\sqrt{3}}=0\)
ĐKXĐ: \(cosx\ne-\dfrac{\sqrt{3}}{2}\) \(\Rightarrow\left[{}\begin{matrix}x\ne\dfrac{5\pi}{6}+k2\pi\\x\ne\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(pt\Rightarrow3-\left(1-2sin^2x\right)+2sinx.cosx-5sinx-cosx=0\)
\(\Leftrightarrow2sin^2x-5sinx+2+cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx-2\right)+cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx+cosx-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx+cosx=2\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Loại nghiệm
\(\Rightarrow x=\dfrac{\pi}{6}+k2\pi\)
\(0\le\dfrac{\pi}{6}+k2\pi\le2022\pi\Rightarrow0\le k\le1010\)
\(\Rightarrow\sum x=1011.\dfrac{\pi}{6}+2\pi\left(0+1+2+...+1010\right)=\dfrac{1011\pi}{6}+2\pi.\dfrac{1010.1011}{2}=...\)
Đúng 2
Bình luận (0)
Tìm m để hàm số \(y=\sqrt{\dfrac{sin2x-cos2x+m-1}{6\left(cos^4x+sin^4x\right)+cos8x+7-5m}}\) xác định với mọi số thực x
\(y=\sqrt{\dfrac{\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)+m-1}{2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}-5m}}\)
Hàm xác định trên R khi:
TH1: \(\left\{{}\begin{matrix}\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)+m-1\ge0\\2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}-5m>0\end{matrix}\right.\) ;\(\forall x\)
\(\Rightarrow\left\{{}\begin{matrix}-m\le\min\limits_R\left(\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)-1\right)=-1-\sqrt{2}\\5m< \min\limits_R\left(2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}\right)=\dfrac{327}{32}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\ge1+\sqrt{2}\\m< \dfrac{327}{160}\end{matrix}\right.\) \(\Rightarrow m\in\varnothing\)
Th2: \(\left\{{}\begin{matrix}\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)+m-1\le0\\2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}-5m< 0\end{matrix}\right.\) ;\(\forall x\)
\(\Rightarrow\left\{{}\begin{matrix}m\le\min\limits_R\left(\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)-1\right)=-1-\sqrt{2}\\5m>\max\limits_R\left(2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}\right)=14\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\le-1-\sqrt{2}\\m>\dfrac{14}{5}\end{matrix}\right.\) \(\Rightarrow m\in\varnothing\)
Đúng 1
Bình luận (1)
Tìm m để GTNN của hàm số \(y=\dfrac{m.cosx+\left(2m-1\right).sinx+3-m}{cosx+sinx-2}\) không quá 3
\(\Leftrightarrow m.cosx+\left(2m-1\right)sinx+3-m=y\left(cosx+sinx-2\right)\)
\(\Leftrightarrow\left(m-y\right)cosx+\left(2m-y-1\right)sinx=m-2y-3\)
Pt có nghiệm khi:
\(\left(m-y\right)^2+\left(2m-y-1\right)^2\ge\left(m-2y-3\right)^2\)
\(\Leftrightarrow2y^2+\left(2m+10\right)y-4m^2-2m+8\le0\)
\(\Rightarrow\dfrac{-m-5-\sqrt{9m^2+14m+9}}{2}\le y\le\dfrac{-m-5+\sqrt{9m^2+14m+9}}{2}\)
\(\Rightarrow y_{min}=\dfrac{-m-5-\sqrt{9m^2+14m+9}}{2}\le3\)
\(\Rightarrow\sqrt{9m^2+14m+9}\ge-m-11\)
BPT này đúng với mọi m. Vậy bài toán thỏa mãn với mọi m
Đúng 2
Bình luận (3)
Tìm tất cả các tham số m để y = \(\sqrt{\dfrac{2sinx+5cosx-13}{2m.sinx+\left(m-1\right)cosx-m-2}}\) xác định với mọi R
\(2sinx+5cosx-13< 0;\forall x\)
\(\Rightarrow\) Hàm xác định trên R khi và chỉ khi:
\(2m.sinx+\left(2m-1\right)cosx-m< 0\) ;\(\forall x\)
\(\Leftrightarrow2m.sinx+\left(2m-1\right).cosx< m\); \(\forall x\)
\(\Rightarrow\dfrac{m}{\sqrt{\left(2m\right)^2+\left(2m-1\right)^2}}>1\)
\(\Rightarrow m\in\varnothing\)
Đúng 2
Bình luận (6)