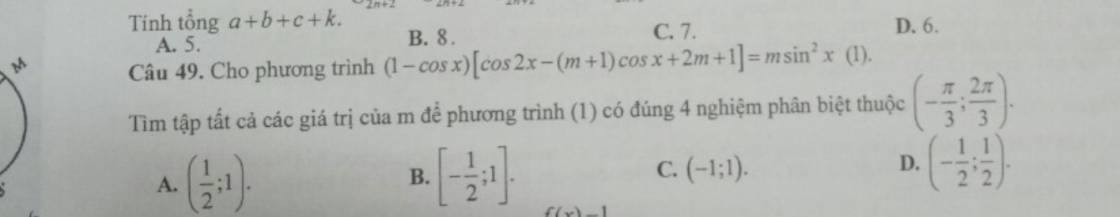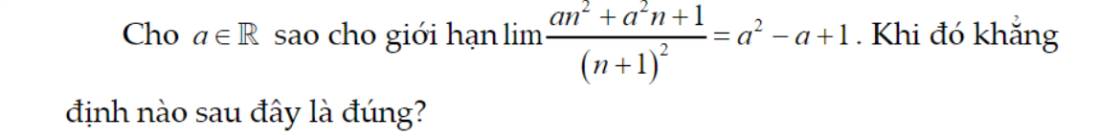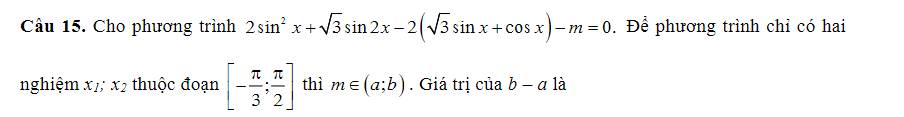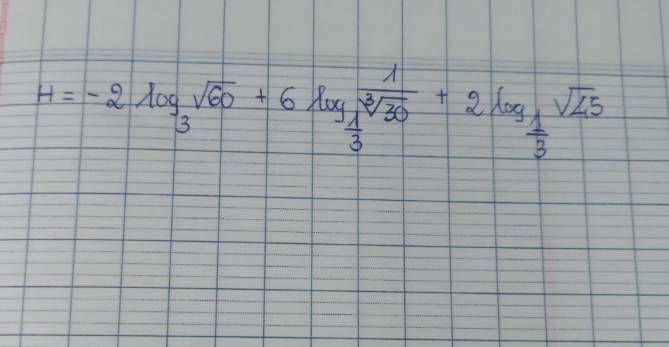Tổng các nghiệm của phương trình \(tan2x=tan\left(\dfrac{\pi}{4}-x\right)\) trên đoạn \(\left[0;3\pi\right]\)
Chương 1: HÀM SỐ LƯỢNG GIÁC. PHƯƠNG TRÌNH LƯỢNG GIÁC
ĐKXĐ: \(x\ne\dfrac{\pi}{4}+k'\dfrac{\pi}{2}\)
pt\(\Leftrightarrow2x=\dfrac{\pi}{4}-x+k\pi\)
\(\Rightarrow x=\dfrac{\pi}{12}+\dfrac{k\pi}{3}\)
\(0\le\dfrac{\pi}{12}+\dfrac{k\pi}{3}\le3\pi\Rightarrow0\le k\le8\)
Loại nghiệm: \(\dfrac{\pi}{4}+\dfrac{k'\pi}{2}\ne\dfrac{\pi}{12}+\dfrac{k\pi}{3}\Rightarrow\dfrac{1+3k'}{2}\ne k\)
Để k nguyên \(\Rightarrow k'\) lẻ \(\Rightarrow k'=2n+1\Rightarrow k\ne\dfrac{3\left(2n+1\right)+1}{2}=3n+2\)
Tới đây ít số thì loại trực triếp \(k=\left\{2;5;8\right\}\) còn nhiều số thì biện luận do \(k\ne3n+2\) nên k có dạng \(k=3n\) hoặc \(k=3n+1\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+\dfrac{3n.\pi}{3}=\dfrac{\pi}{12}+n\pi\\x=\dfrac{\pi}{12}+\dfrac{\left(3n+1\right)\pi}{3}=\dfrac{5\pi}{12}+n\pi\end{matrix}\right.\)
Đúng 2
Bình luận (0)
ĐKXĐ: \(\left\{{}\begin{matrix}2x\ne\dfrac{\Omega}{2}+k\Omega\\\dfrac{\Omega}{4}-x\ne\dfrac{\Omega}{2}+k\Omega\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\ne\dfrac{\Omega}{4}+\dfrac{k\Omega}{2}\\x\ne-\dfrac{\Omega}{4}-k\Omega\end{matrix}\right.\)
=>\(x\ne\dfrac{\Omega}{4}+\dfrac{k\Omega}{2}\)
\(tan2x=tan\left(\dfrac{\Omega}{4}-x\right)\)
=>\(2x=\dfrac{\Omega}{4}-x+k\Omega\)
=>\(3x=\dfrac{\Omega}{4}+k\Omega\)
=>\(x=\dfrac{\Omega}{12}+\dfrac{k\Omega}{3}\)
mà \(x\in\left[0;3\Omega\right]\)
nên \(\dfrac{\Omega}{12}+\dfrac{k\Omega}{3}\in\left[0;3\Omega\right]\)
=>\(\dfrac{1}{12}+\dfrac{k}{3}\in\left[0;3\right]\)
=>\(\dfrac{k}{3}\in\left[-\dfrac{1}{12};\dfrac{35}{12}\right]\)
=>\(k\in\left[-\dfrac{1}{4};\dfrac{35}{4}\right]\)
mà k nguyên
nên \(k\in\left\{0;1;2;3;4;5;6;7;8\right\}\)
=>\(\dfrac{\Omega}{12}+\dfrac{k\Omega}{3}\in\left\{\dfrac{1}{12}\Omega;\dfrac{5}{12}\Omega;\dfrac{3}{4}\Omega;\dfrac{13}{12}\Omega;\dfrac{17}{12}\Omega;\dfrac{7}{4}\Omega;\dfrac{25}{12}\Omega;\dfrac{29}{12}\Omega;\dfrac{11}{4}\Omega\right\}\)
=>\(x\in\left\{\dfrac{1}{12}\Omega;\dfrac{5}{12}\Omega;\dfrac{3}{4}\Omega;\dfrac{13}{12}\Omega;\dfrac{17}{12}\Omega;\dfrac{7}{4}\Omega;\dfrac{25}{12}\Omega;\dfrac{29}{12}\Omega;\dfrac{11}{4}\Omega\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{\dfrac{1}{12}\Omega;\dfrac{5}{12}\Omega;\dfrac{13}{12}\Omega;\dfrac{17}{12}\Omega;\dfrac{25}{12}\Omega;\dfrac{29}{12}\Omega\right\}\)
Tổng các nghiệm là:
\(\Omega\left(\dfrac{1}{12}+\dfrac{5}{12}+\dfrac{13}{12}+\dfrac{17}{12}+\dfrac{25}{12}+\dfrac{29}{12}\right)=\dfrac{15}{2}\Omega\)
Đúng 0
Bình luận (0)
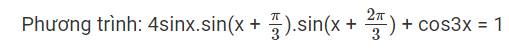
Tính tổng số nghiệm của phương trình trong khoảng \(\left[0;5\pi\right]\)
\(\Leftrightarrow2sinx\left(cos\dfrac{\pi}{3}-cos\left(2x+\pi\right)\right)+cos3x=1\)
\(\Leftrightarrow2sinx\left(\dfrac{1}{2}+cos2x\right)+cos3x=1\)
\(\Leftrightarrow sinx+2sinx.cos2x+cos3x=1\)
\(\Leftrightarrow sinx+sin3x-sinx+cos3x=1\)
\(\Leftrightarrow sin3x+cos3x=1\)
\(\Leftrightarrow sin\left(3x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
Đúng 2
Bình luận (5)
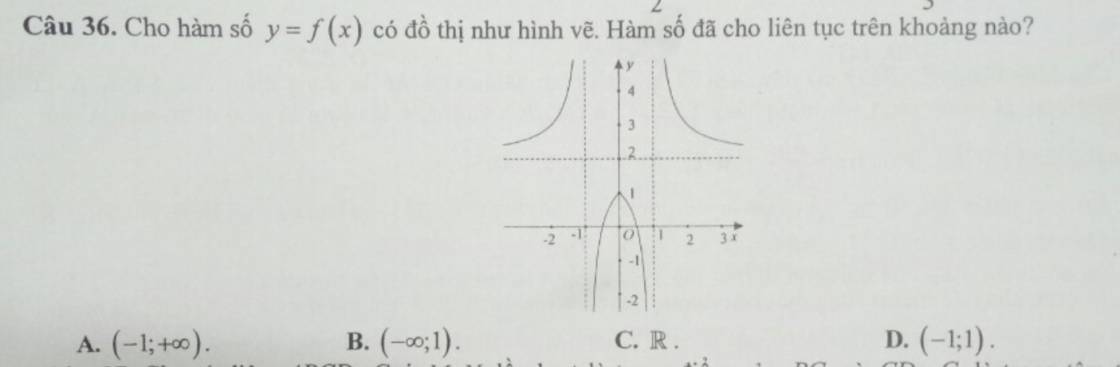
Nhìn đồ thị thì hàm số liên tục trên các khoảng \(\left(-\infty;-1\right);\left(-1;1\right);\left(1;+\infty\right)\) cũng như các khoảng con của chúng
Đúng 1
Bình luận (0)
\(\Leftrightarrow\left(1-cosx\right)\left(cos2x-\left(m+1\right)cosx+2m+1\right)=m\left(1-cosx\right)\left(1+cosx\right)\)
TH1: \(cosx=1\)
TH2: \(cos2x-\left(m+1\right)cosx+2m+1=m\left(1+cosx\right)\)
\(\Leftrightarrow2cos^2x-cosx-2m.cosx+m=0\)
\(\Leftrightarrow cosx\left(2cosx-1\right)-m\left(2cosx-1\right)=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(cosx-m\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=m\end{matrix}\right.\)
Đường tròn lượng giác là xong.
Đúng 2
Bình luận (0)
Có bao nhiêu giá trị nguyên của m để phương trình \(8sin^2x+2\left(5-m\right)sinx-m+3=0\) có đúng 8 nghiệm phân biệt thuộc \(\left[-\pi;2\pi\right]\)
\(8sin^2x+10sinx+3-m\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx+1\right)\left(4sinx+3\right)-m\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx+1\right)\left(4sinx-m+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=-\dfrac{1}{2}\\sinx=\dfrac{m-3}{4}\end{matrix}\right.\)
Tới đây dùng đường tròn lượng giác là ra
Đúng 2
Bình luận (0)
\(\lim\dfrac{an^2+a^2n+1}{\left(n+1\right)^2}=a\)
\(\Rightarrow a^2-a+1=a\Rightarrow a=1\)
Đúng 1
Bình luận (0)
Đặt \(\sqrt{3}sinx+cosx=2sin\left(x+\dfrac{\pi}{6}\right)=t\in\left[-2;2\right]\)
\(x\in\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\Rightarrow x+\dfrac{\pi}{6}\in\left[-\dfrac{\pi}{3};\dfrac{2\pi}{3}\right]\)
\(\Rightarrow t^2=3sin^2x+cos^2x+2\sqrt{3}sinx.cosx=2sin^2x+\sqrt{3}sin2x+1\)
Pt trở thành:
\(t^2-1-2t-m=0\Rightarrow t^2-2t-1=m\) (1)
Từ đường tròn lượng giác, các trường hợp thỏa mãn:
TH1: (1) có 2 nghiệm thỏa mãn: \(\left\{{}\begin{matrix}\sqrt{3}\le t_1< 2\\\left[{}\begin{matrix}t_2>2\\t_2< -\sqrt{3}\end{matrix}\right.\end{matrix}\right.\)
TH2: (1) có 2 nghiệm pb sao cho \(-\sqrt{3}\le t_1< t_2\le\sqrt{3}\)
Tới đây dùng đồ thị là xong thôi
Đúng 2
Bình luận (0)
Nghiệm của phương trình \(sin^4x+cos^4x+cos\left(x-\dfrac{\pi}{4}\right).sin\left(3x-\dfrac{\pi}{4}\right)-\dfrac{3}{2}=0\)
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x+\dfrac{1}{2}sin\left(4x-\dfrac{\pi}{2}\right)+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^22x-\dfrac{1}{2}cos4x+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)
\(\Leftrightarrow1-\dfrac{1}{2}\left(\dfrac{1-cos4x}{2}\right)-\dfrac{1}{2}cos4x+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)
\(\Leftrightarrow-\dfrac{3}{4}-\dfrac{1}{4}cos4x+\dfrac{1}{2}sin2x=0\)
\(\Leftrightarrow-\dfrac{3}{4}-\dfrac{1}{4}\left(1-2sin^22x\right)+\dfrac{1}{2}sin2x=0\)
\(\Leftrightarrow...\)
Đúng 2
Bình luận (0)
Xác định m để phương trình \(6cos^2x+\left(9m-7\right).cosx-6m+2=0\) có đúng 3 nghiệm phân biệt \(x\in\left(0;\dfrac{3\pi}{2}\right)\)
Đặt \(cosx=t\in\left[-1;1\right]\)
\(\Rightarrow6t^2+\left(9m-7\right)t-6m+2=0\)
\(\Leftrightarrow6t^2-7t+2+9mt-6m=0\)
\(\Leftrightarrow\left(2t-1\right)\left(3t-2\right)+3m\left(3t-2\right)=0\)
\(\Leftrightarrow\left(3t-2\right)\left(2t+3m-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=\dfrac{2}{3}\\cosx=\dfrac{-3m+1}{2}\end{matrix}\right.\)
(Chà tới đây mới thấy ko cần đặt ẩn phụ, nhìn con số 9m và 6m to 1 cách vô lý đã nghi nghi có gì đó bất thường trong nghiệm :D)
Pt \(cosx=\dfrac{2}{3}\) cho 1 nghiệm thuộc \(\left(0;\dfrac{\pi}{2}\right)\)
Để pt có 3 nghiệm pb thì \(cosx=\dfrac{-3m+1}{2}\) cho 2 nghiệm pb thuộc khoảng đã cho
Từ đường tròn lượng giác ta dễ dàng suy ra: \(-1< \dfrac{-2m+1}{2}< 0\)
Đúng 2
Bình luận (2)
\(H=-2log_3\sqrt{60}+6log_{3^{-1}}\dfrac{1}{\sqrt[3]{30}}+2log_{3^{-1}}\sqrt{45}\)
\(=-log_3\left(\sqrt{60}\right)^2-log_3\left(\dfrac{1}{\sqrt[3]{30}}\right)^6-log_3\left(\sqrt{45}\right)^2\)
\(=-\left(log_360+log_3\dfrac{1}{900}+log_345\right)\)
\(=-log_3\dfrac{60.45}{900}=-log_33=-1\)
Đúng 2
Bình luận (0)