Số giá trị nguyên của m để phương trình \(2sin^2x-sinx.cosx-m.cos^2x=1\) có nghiệm trên \(\left[-\dfrac{\pi}{4};\dfrac{\pi}{4}\right]\) là?
Chương 1: HÀM SỐ LƯỢNG GIÁC. PHƯƠNG TRÌNH LƯỢNG GIÁC
Cho phương trình (1-cosx)[cos2x-(m+1)cosx+2m+1]=\(msin^2x\) (1)
Tìm tập tất cả các giá trị của m để pt (1) có đúng 4 nghiệm phân biệt thuộc \(\left(\dfrac{-\pi}{3};\dfrac{2\pi}{3}\right)\)
Cho hàm số \(f\left(x\right)=\dfrac{sinx}{sinx+cosx}\). Tính giá trị của biểu thức \(T=f\left(\dfrac{\pi}{2024}\right)+f\left(\dfrac{2\pi}{2024}\right)+f\left(\dfrac{3\pi}{2024}\right)+...+f\left(\dfrac{1011\pi}{2024}\right)\)
\(f\left(x\right)+f\left(\dfrac{\pi}{2}-x\right)=\dfrac{sinx}{sinx+cosx}+\dfrac{sin\left(\dfrac{\pi}{2}-x\right)}{sin\left(\dfrac{\pi}{2}-x\right)+cos\left(\dfrac{\pi}{2}-x\right)}\)
\(=\dfrac{sinx}{sinx+cosx}+\dfrac{cosx}{cosx+sinx}=1\)
\(\Rightarrow T=f\left(\dfrac{\pi}{2024}\right)+f\left(\dfrac{1011\pi}{2024}\right)+...+f\left(\dfrac{505\pi}{2024}\right)+f\left(\dfrac{507\pi}{2024}\right)+f\left(\dfrac{506\pi}{2024}\right)\)
\(=1+1+...+1+f\left(\dfrac{\pi}{4}\right)\) (505 số 1)
\(=505+\dfrac{sin\left(\dfrac{\pi}{4}\right)}{sin\left(\dfrac{\pi}{4}\right)+cos\left(\dfrac{\pi}{4}\right)}=505+\dfrac{1}{2}=...\)
Đúng 2
Bình luận (0)
Có bao nhiêu số nguyên m để phương trình: \(4sin2x+\sqrt{3}.m=2\left(msinx+2\sqrt{3}.cosx\right)\) có đúng 5 nghiệm phân biệt thuộc khoảng \(\left(0;\dfrac{5\pi}{2}\right)\)
\(8sinx.cosx-4\sqrt{3}cosx=m\left(2sinx-\sqrt{3}\right)\)
\(\Leftrightarrow4cosx\left(2sinx-\sqrt{3}\right)-m\left(2sinx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left(4cosx-m\right)\left(2sinx-\sqrt{3}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=\dfrac{\sqrt{3}}{2}\\cosx=\dfrac{m}{4}\end{matrix}\right.\)
\(sinx=\dfrac{\sqrt{3}}{2}\) có 3 nghiệm \(x=\left\{\dfrac{\pi}{3};\dfrac{2\pi}{3};\dfrac{7\pi}{3}\right\}\) trên khoảng đã cho
Nên pt có đúng 5 nghiệm trên khoảng cho \(cosx=\dfrac{m}{4}\) có 2 nghiệm (và khác các nghiệm nói trên)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{m}{4}\ne\dfrac{1}{2}\\0< \dfrac{m}{4}< 1\end{matrix}\right.\) \(\Rightarrow m=\left\{1;3\right\}\)
Đúng 2
Bình luận (1)
Có bao nhiêu số nguyên m để phương trình: \(4sin2x+\sqrt{3}.m=2\left(msinx+2\sqrt{3}.cosx\right)\) có đúng 5 nghiệm phân biệt thuộc khoảng \(\left(0;\dfrac{5\pi}{2}\right)\)
Tìm m để hàm số \(y=\dfrac{3x}{\sqrt{2sin^2x-sinx-m}}\) xác định trên R
Hàm xác định trên R khi \(2sin^2x-sinx-m>0\) ; \(\forall x\)
\(\Leftrightarrow m< 2sin^2x-sinx\)
\(\Rightarrow m< min_{x\in R}f\left(x\right)\)
Với \(f\left(x\right)=2sin^2x-sinx=2\left(sinx-\dfrac{1}{4}\right)^2-\dfrac{1}{8}\ge-\dfrac{1}{8}\)
\(\Rightarrow m< -\dfrac{1}{8}\)
Đúng 1
Bình luận (0)
Biết rằng khi \(m=m_0\) thì phương trình: \(2sin^2\left(x\right)-\left(5m+1\right)sinx+2m^2+2m=0\) có đúng 2 nghiệm phân biệt thuộc khoảng \(\left(-\dfrac{\pi}{2};3\pi\right)\). Tìm \(m_0\)
Biết rằng khi mm0��0 thì phương trình 2sin2x−(5m+1)sinx+2m2+2m02sin2�−(5�+1)sin�+2�2+2�0 có đúng 55 nghiệm phân biệt thuộc khoảng (−π2;3π)(−�2;3�). Tìm m_0.
Đọc tiếp
Biết rằng khi thì phương trình có đúng nghiệm phân biệt thuộc khoảng . Tìm \(m_0\).
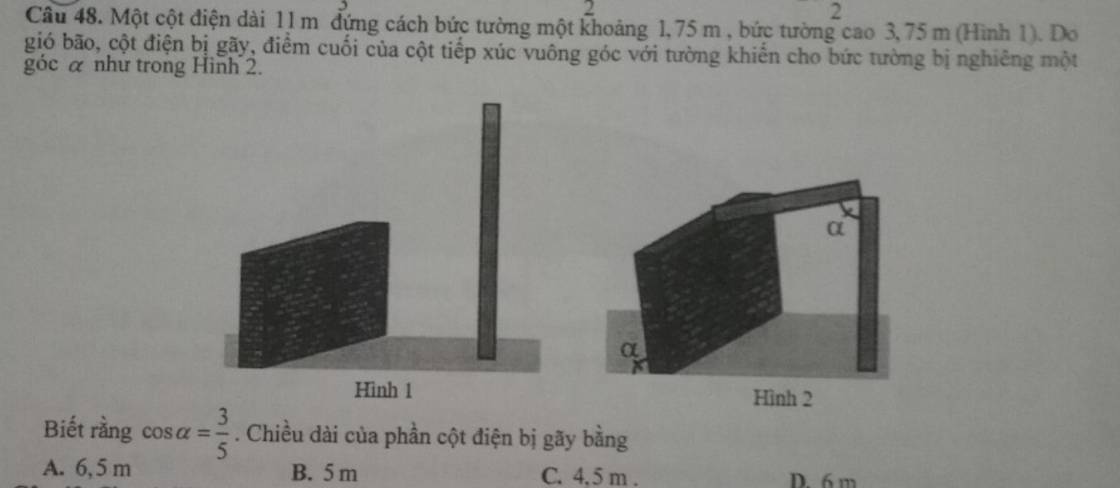
Kẻ DE vuông góc AB và DF vuông góc AC (D là đỉnh cột điện)
\(EA=AD.cos\alpha=3,75.\dfrac{3}{5}=2,25\)
\(\Rightarrow DF=BE=1,75+2,25=4\)
\(\Rightarrow DC=\dfrac{DF}{sin\alpha}=\dfrac{4}{\sqrt{1-\left(\dfrac{3}{5}\right)^2}}=5\)
Đúng 2
Bình luận (0)