Cho S.ABCD có đáy hình thang vuông tại A và B, AD=2a, AB= BC = a, SA vuông góc với mặt phẳng đáy. Biết SC tạo với mặt phẳng đáy một góc bằng 60o. Tính góc giữa SD và mặt phẳng (SAC)?
Bài 6: Ôn tập chương Vecơ trong không gian. Quan hệ vuông góc trong không gian.
Cho ΔSAB đều và hình vuông ABCD nằm trong 2 mặt phẳng vuông góc nhau. Tính góc giữa SC và (ABCD)?
Cho chóp S.ABCD có đáy là hình vuông cạnh a, SA⊥(ABCD), SA=\(a\sqrt{6}\). Tính góc α giữa đường SC và mặt phẳng (SAD)
CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
=>(SC;(SAD))=(SC;SD)=góc DSC
SD=căn SA^2+AD^2=a*căn 7
DC=a
SC=căn SA^2+AC^2=3a
\(cosDSC=\dfrac{SD^2+SC^2-DC^2}{2\cdot SD\cdot SC}=\dfrac{9a^2+7a^2-a^2}{2\cdot3a\cdot a\sqrt{7}}=\dfrac{5\sqrt{7}}{14}\)
=>góc DSC=19 độ
Đúng 0
Bình luận (0)
Cho chóp S.ABCD có mặt phẳng đáy là hình vuông cạnh a, ΔSAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính góc giữa SC và AD ?
Cho lăng trụ đều ABC.A'B'C' có AB=1, AA'=m(m>0). Hỏi m bằng bao nhiêu để góc giữa AB' và BC' bằng 60o ?
Cho chóp S.ABCD có mặt phẳng đáy là hình vuông cạnh a, SA=\(a\sqrt{3}\), SA vuông góc với mặt phẳng đáy. Tính góc giữa SB và AC ?
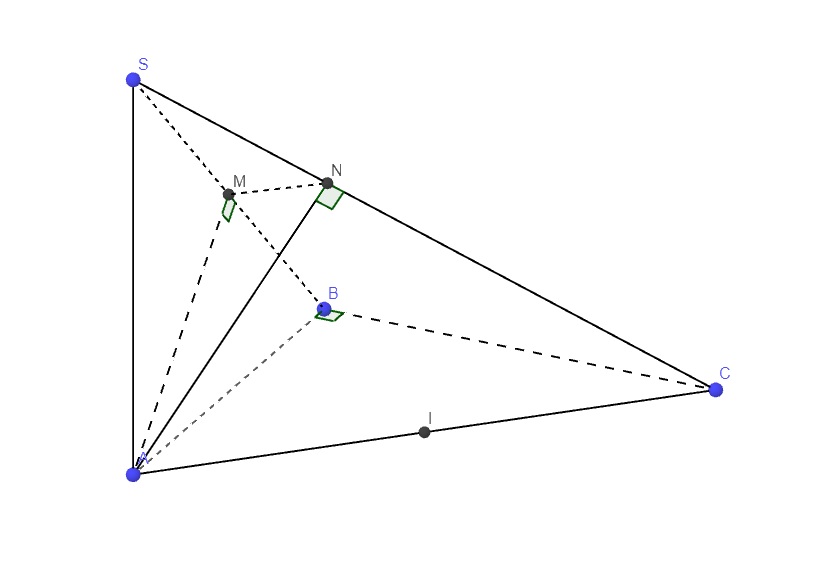
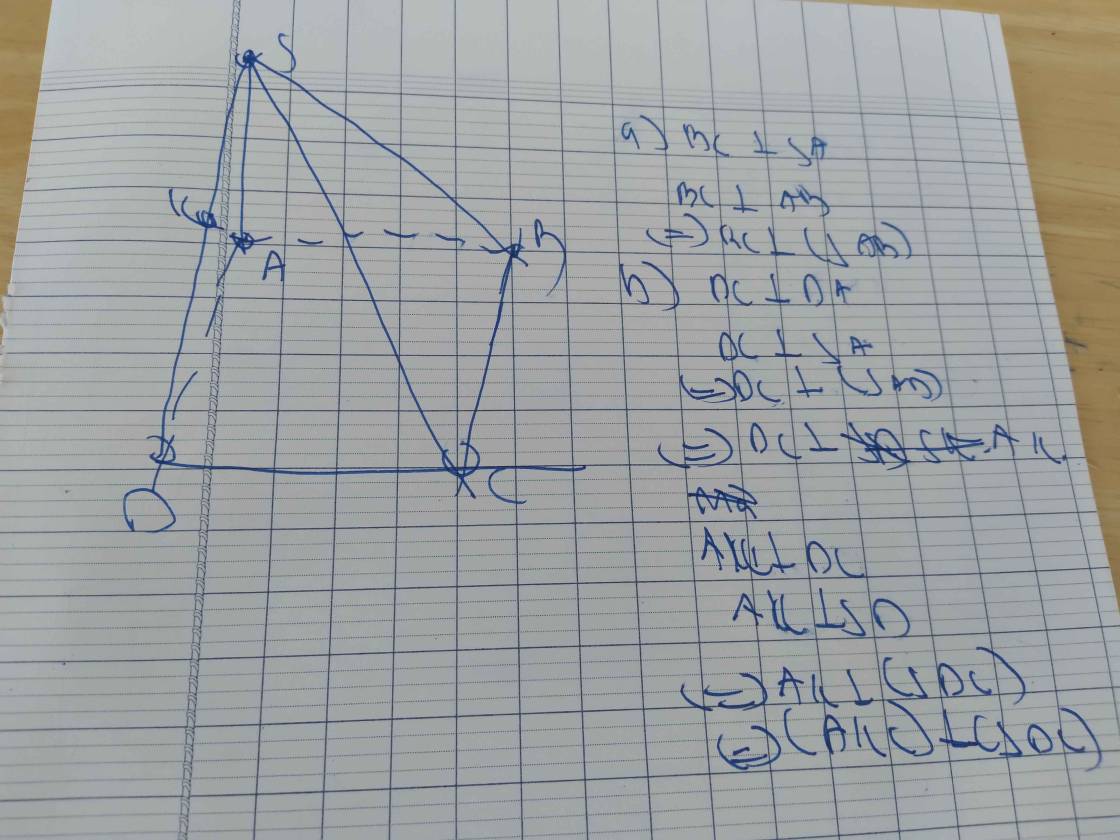
Câu 5: Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O cạnh bằng a, góc giữa cạnh bên và mặt đáy 1 góc 60°. Gọi IE lần lượt là là trung điểm của cạnh BC,CD a)Chứng minh: AC vuông góc (SBD) ; BD vuông góc SA b)Chứng minh: (SBC) vuông góc (SOI) c)Tính góc giữa mặt bên và mặt đáy. d)góc giữa OE và mặt (SCD) e)Tính khoảng cách giữa SI và AB.
a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)
Đúng 0
Bình luận (0)
1/ Cho left|overrightarrow{u}right|sqrt{2} , left|overrightarrow{v}right|10 , overrightarrow{u}.overrightarrow{v}10. Tính số đó góc hợp giữa overrightarrow{u}vàoverrightarrow{v} . 2/ Cho hình chóp S.ABC, đáy là tâm giác vuông cân tại B, SA vuông góc với mặt đáy, AB SA aa. Tính góc 2mp ((SBC),(ABC))b. Gọi M,N lần lượt là hình chiếu của A lên SB, SC. Tam giác AMN là tam giác gì? tính góc giữa 2mp ((AMN),(ABC)), góc giữa (AC;(AMN)).c. Tính khoảng cách từ trung điểm I của đoạn thẳng AC đến mp (SBC...
Đọc tiếp
1/ Cho \(\left|\overrightarrow{u}\right|=\sqrt{2}\) , \(\left|\overrightarrow{v}\right|=10\) , \(\overrightarrow{u}.\overrightarrow{v}=10\). Tính số đó góc hợp giữa \(\overrightarrow{u}và\overrightarrow{v}\) .
2/ Cho hình chóp S.ABC, đáy là tâm giác vuông cân tại B, SA vuông góc với mặt đáy, AB = SA = a
a. Tính góc 2mp ((SBC),(ABC))
b. Gọi M,N lần lượt là hình chiếu của A lên SB, SC. Tam giác AMN là tam giác gì? tính góc giữa 2mp ((AMN),(ABC)), góc giữa (AC;(AMN)).
c. Tính khoảng cách từ trung điểm I của đoạn thẳng AC đến mp (SBC)
3/ Cho hình chóp S.ABCD, đáy là hình vuống tâm O, SA = SB = SC = SD = AB = 2a. M,N lần lượt là trung điểm SB, SD.
a. Tính số đo của góc giữa (MN;SC)
b. SA vuống góc với đường thẳng nào?
c. Tính a khoảng cách giữa d(AB;(SCD)).
CỨU MK VS, MAI MK KT 15' mà mk lại ko lm đc, ko bt lm lun, giúp mk vs, cảm ơn nhiều.
1.
\(cos\left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)=\dfrac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}=\dfrac{10}{10.\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)
\(\Rightarrow\left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)=45^0\)
2.
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\) (1)
Mà \(BC=\left(SBC\right)\cap\left(ABC\right)\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABC)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=1\Rightarrow\widehat{SBA}=45^0\)
b.
Từ (1) \(\Rightarrow BC\perp AM\)
Mà \(AM\perp SB\left(gt\right)\) \(\Rightarrow AM\perp\left(SBC\right)\) (2)
\(\Rightarrow AM\perp MN\Rightarrow\Delta AMN\) vuông tại M
Từ (2) \(\Rightarrow AM\perp SC\), mà \(SC\perp AN\left(gt\right)\)
\(\Rightarrow SC\perp\left(AMN\right)\) (3)
Lại có \(SA\perp\left(ABC\right)\) theo giả thiết
\(\Rightarrow\) Góc giữa (AMN) và (ABC) bằng góc giữa SA và SC hay là góc \(\widehat{ASC}\)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{ASC}=\dfrac{AC}{SA}=\sqrt{2}\Rightarrow\widehat{ASC}\approx54^044'\)
Từ (3) \(\Rightarrow AN\) là hình chiếu vuông góc của AC lên (AMN)
\(\Rightarrow\widehat{CAN}\) là góc giữa AC và (AMN)
Mà \(\widehat{CAN}=\widehat{ASC}\) (cùng phụ \(\widehat{ACS}\)) \(\Rightarrow\widehat{CAN}=...\)
c.
\(\left\{{}\begin{matrix}IC=\dfrac{1}{2}AC\left(gt\right)\\AI\cap\left(SBC\right)=C\end{matrix}\right.\) \(\Rightarrow d\left(I;\left(SBC\right)\right)=\dfrac{1}{2}d\left(A;\left(SBC\right)\right)\)
Mà từ (2) ta có \(AM\perp\left(SBC\right)\Rightarrow AM=d\left(A;\left(SBC\right)\right)\)
\(SA=AB\left(gt\right)\Rightarrow\Delta SAB\) vuông cân tại A
\(\Rightarrow AM=\dfrac{1}{2}SB=\dfrac{a\sqrt{2}}{2}\Rightarrow d\left(I;\left(SBC\right)\right)=\dfrac{1}{2}AM=\dfrac{a\sqrt{2}}{4}\)
Đúng 1
Bình luận (0)
3.
a.
Do \(SA=SB=SC=SD\Rightarrow\) hình chiếu vuông góc của S lên (ABCD) trùng tâm O của hình vuông
Hay \(SO\perp\left(ABCD\right)\)
\(\Rightarrow SO\perp BD\)
Lại có \(AC\perp BD\) (hai đường chéo hình vuông)
\(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp SC\)
Mà MN là đường trung bình tam giác SBD \(\Rightarrow MN||BD\)
\(\Rightarrow MN\perp SC\Rightarrow\left(\widehat{MN;SC}\right)=90^0\)
b.
\(AC=\sqrt{AB^2+BC^2}=2a\sqrt{2}\)
\(SA=SC=2a\Rightarrow SA^2+SC^2=8a^2=AC^2\)
\(\Rightarrow\Delta SAC\) vuông tại S (pitago đảo)
\(\Rightarrow SA\perp SC\)
c.
\(AB||CD\Rightarrow AB||\left(SCD\right)\Rightarrow d\left(AB;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)\)
Lại có \(\left\{{}\begin{matrix}AC=2OC\\AO\cap\left(SCD\right)=C\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)\)
Từ O kẻ \(OE\perp CD\), từ \(O\) kẻ \(OF\perp SE\)
\(\Rightarrow OF\perp\left(SCD\right)\Rightarrow OF=d\left(O;\left(SCD\right)\right)\)
\(OE=\dfrac{1}{2}BC=a\) (đường trung bình)
\(\Delta SAC\) vuông tại S (theo cm câu b) \(\Rightarrow SO=\dfrac{1}{2}AC=a\sqrt{2}\) (trung tuyến ứng với cạnh huyền)
Hệ thức lượng:
\(OF=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{6}}{3}\)
\(\Rightarrow d\left(A;\left(SCD\right)\right)=2OF=\dfrac{2a\sqrt{6}}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Hình chóp SABCD có ABCD là hình vuông, SA vuông ABCDa) (SAD) vuông (ABCD)b) SA=SB=SC=SDc) (SAB) vuông (ABCD)(SAD) vuông (ABCD
Xem chi tiết
a: AB vuông góc AD
AB vuông góc SA
=>AB vuông góc (SAD)
=>(ABCD) vuông góc (SAD)
c: AD vuông góc AB
AD vuông góc SA
=>AD vuông góc (SAB)
=>(ABCD) vuông góc (SAB)
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có đáy là hình vuông cạnh = a. SA vuông góc với (ABCD), SA=a. a)Chứng minh BC vuông góc với (SAB)? b)Gọi K là chân đường cao hạ từ A lên SD. Chứng minh (AKC) vuông góc với (SDC)?