TN
20 tháng 11 2023 lúc 20:11
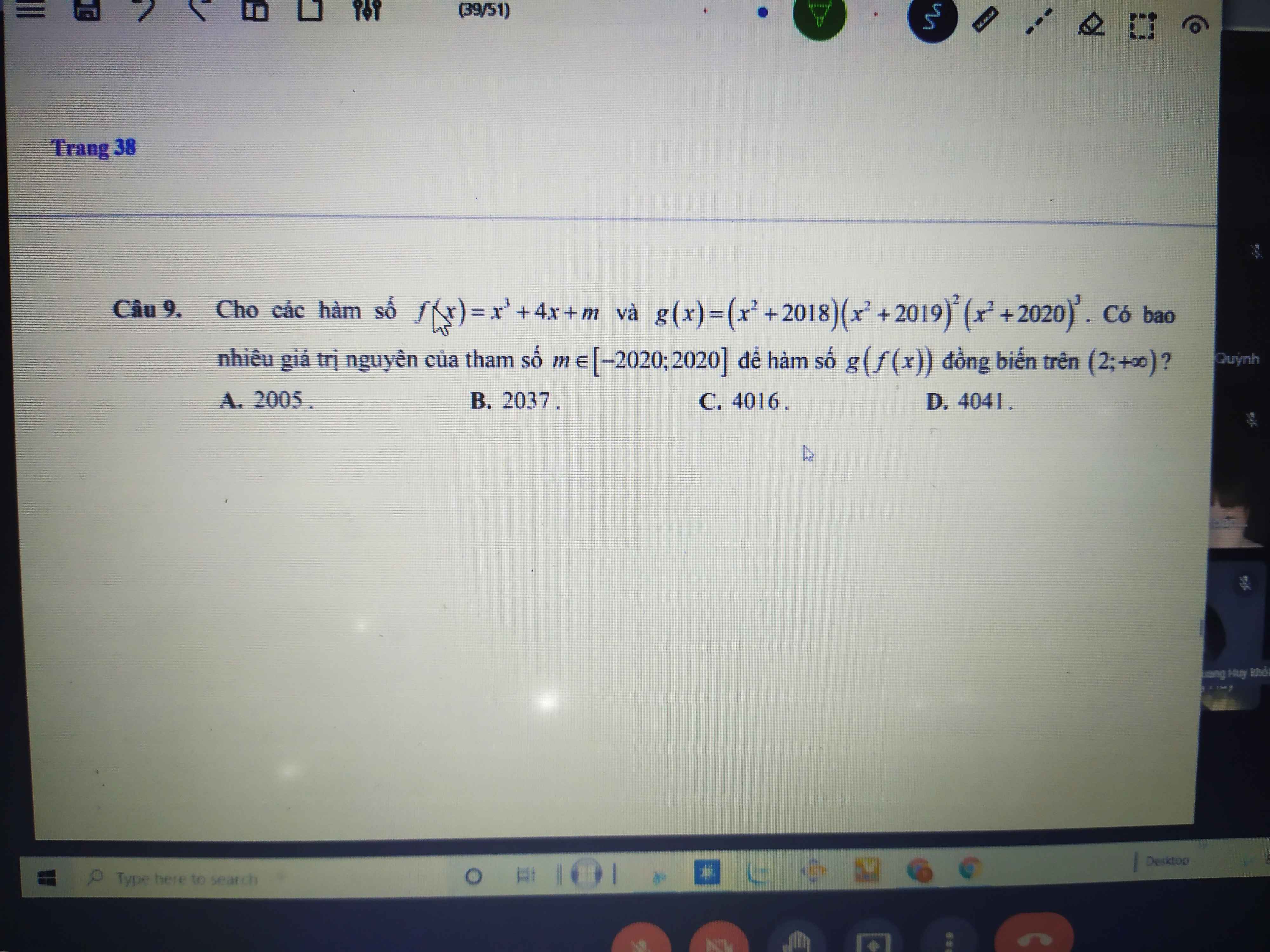
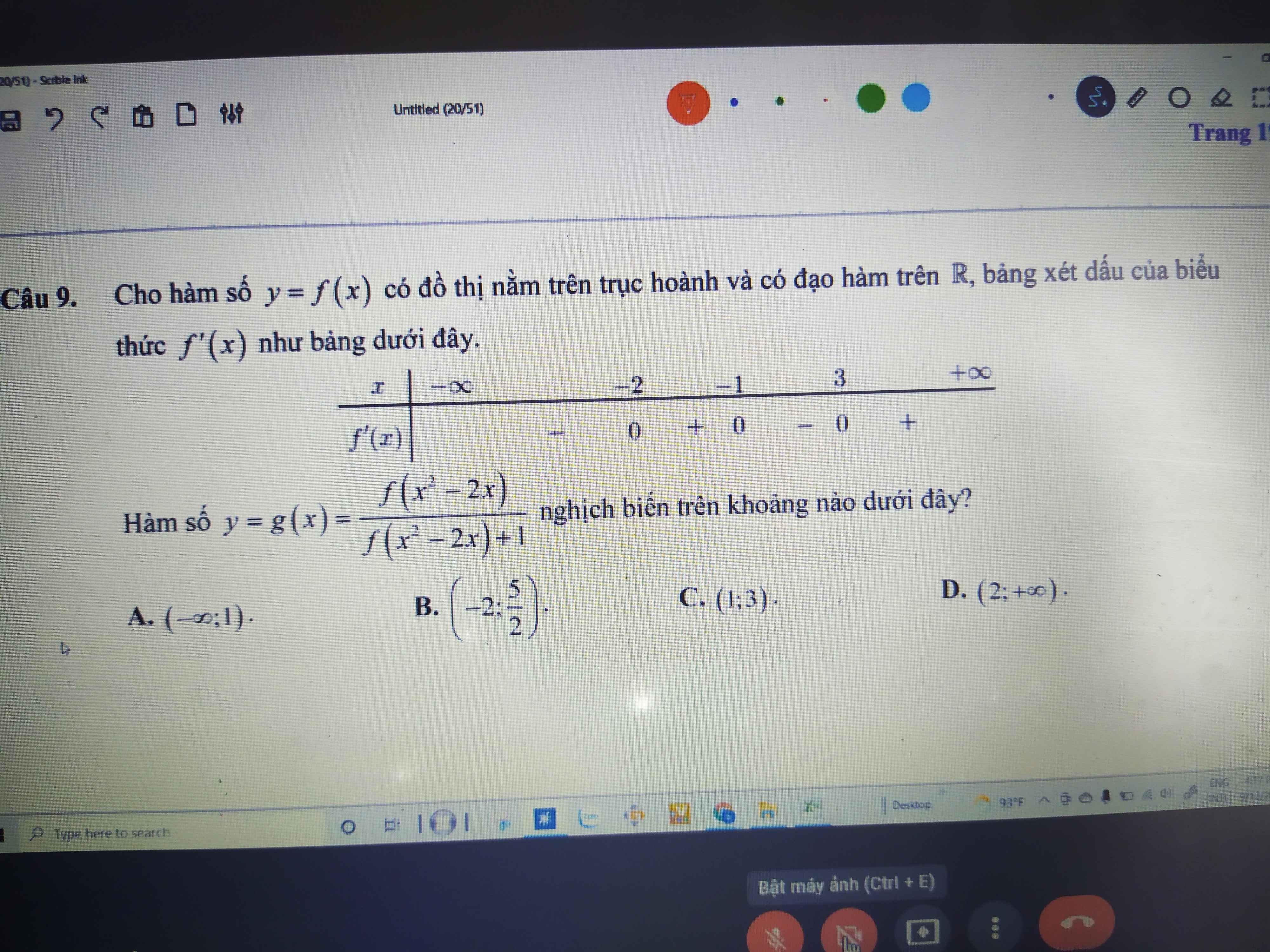
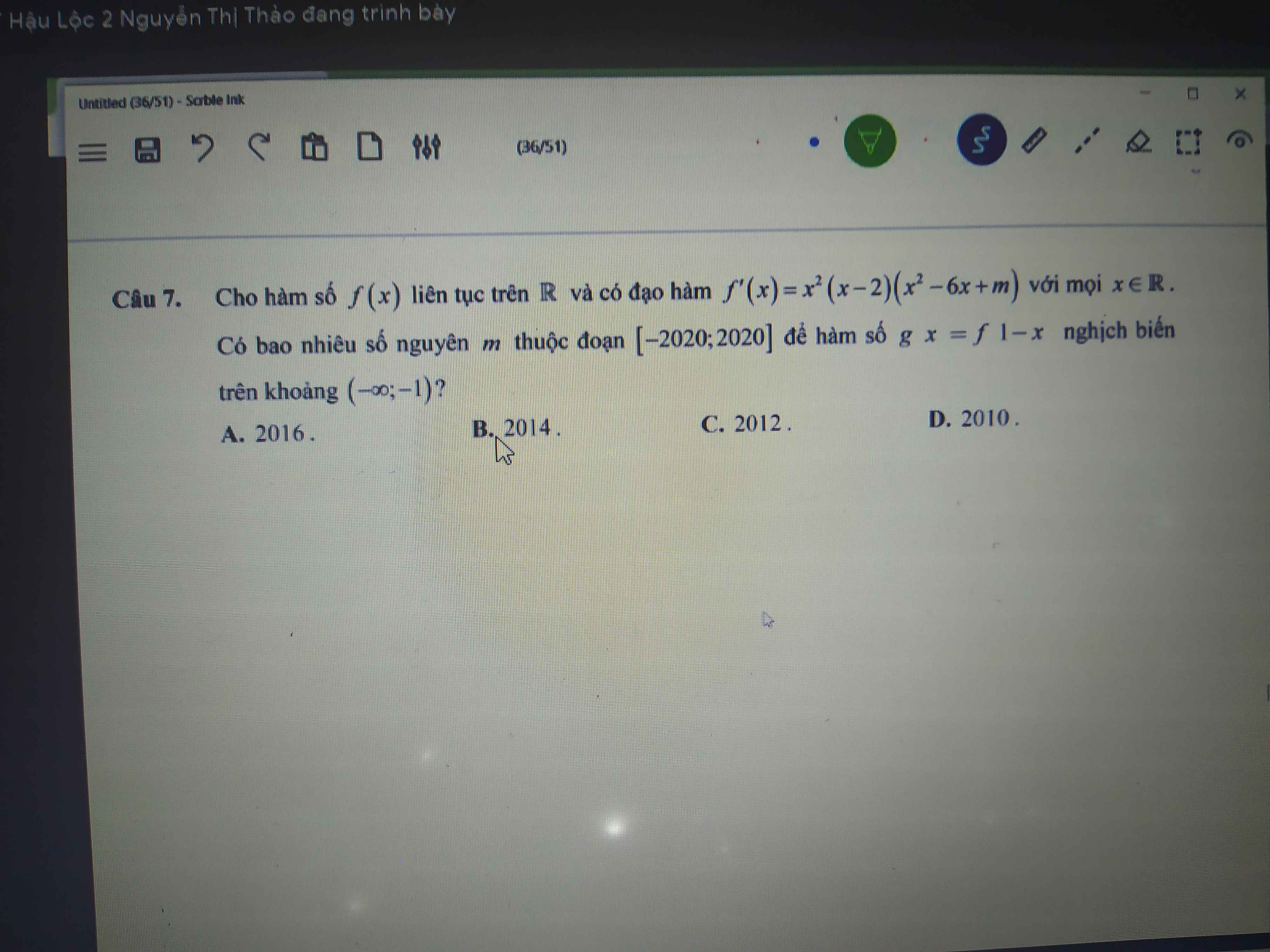
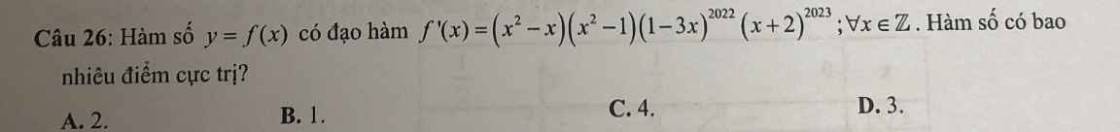\(f'\left(x\right)=\left(x^2-x\right)\left(x^2-1\right)\left(1-3x\right)^{2022}\left(x+2\right)^{2023}\)
=>\(f'\left(x\right)=x\left(1-3x\right)^{2022}\left(x^2-1\right)\cdot\left(x+2\right)^{2022}\cdot\left(x-1\right)\left(x+2\right)\)
Chúng ta sẽ loại \(x;\left(1-3x\right)^{2022};\left(x^2-1\right);\left(x+2\right)^{2022}\) vì đây là những đa thức có bậc chẵn
=>Còn lại x-1;x+2
=>f(x) sẽ có 2 cực trị
=>Chọn A
Đúng 0
Bình luận (0)
