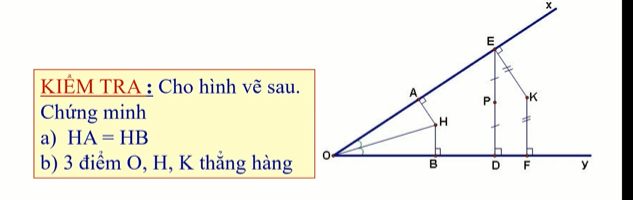
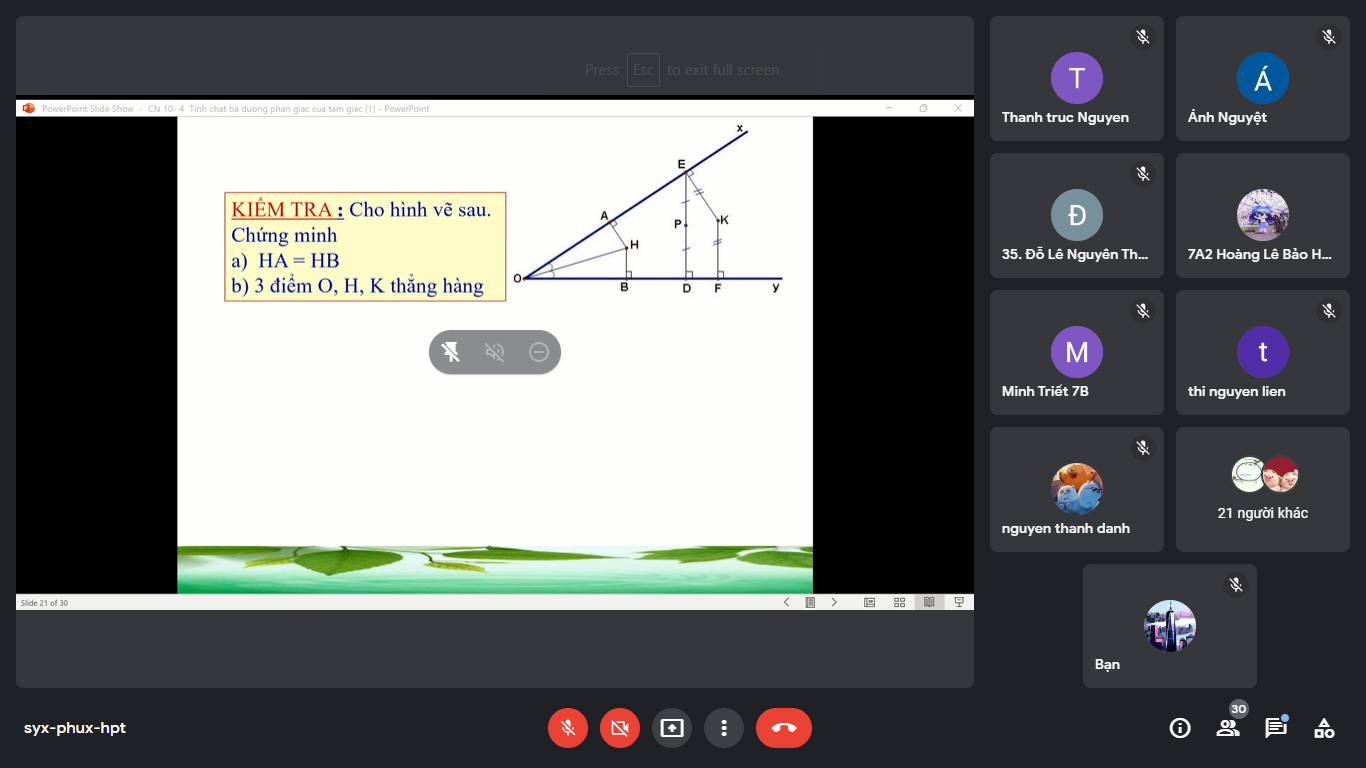
Bài 5: Tính chất đường phân giác của một góc

Cô sắp kt đến r gấp

-Sửa đề: 2 đg p/g góc tại đỉnh B và C....

-△ABC có: \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)

\(\Rightarrow80^0+\widehat{ABC}+\widehat{ACB}=180^0\)

\(\Rightarrow\widehat{ABC}+\widehat{ACB}=100^0\)

\(\Rightarrow180^0-\widehat{CBx}+180^0-\widehat{BCy}=100^0\) (Bx là tia đối của BA, Cy là tia đối của CA).

\(\Rightarrow\widehat{CBx}+\widehat{BCy}=260^0\)

\(\Rightarrow2\widehat{CBK}+2\widehat{BCK}=260^0\)

\(\Rightarrow\widehat{CBK}+\widehat{BCK}=130^0\)

△BCK có: \(\widehat{BKC}+\widehat{CBK}+\widehat{BCK}=180^0\)

\(\Rightarrow\widehat{BKC}+130^0=180^0\)

\(\Rightarrow\widehat{BKC}=50^0\)

4:

a: AC=căn 10^2-6^2=8cm

b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có

BE chung

góc ABE=góc HBE

=>ΔBAE=ΔBHE

=>BA=BH và EA=EH<EC

c: Xét ΔBKC có

CA,KH là đường cao

CA cắt KH tại E

=>E là trực tâm

=>BE vuông góc KC

BE vuông góc KC

BE vuông góc AH

=>KC//AH

d: BA=BH; góc ABH=60 độ

=>ΔBAH đều

a: Xét ΔABD và ΔACE có

góc ABD=góc ACE

AB=AC

góc BAD chung

=>ΔABD=ΔACE

=>BD=CE

b: Xét ΔADE có AD=AE

nên ΔADE cân tại A

c: Xét ΔABC có AE/AB=AD/AC

nên ED//BC

a: XétΔABD và ΔACD có

AB=AC
AD chung

BD=CD

Do đó:ΔABD=ΔACD

b: Ta có: ΔABC cân tại A

mà AD là đường trung tuyến

nên AD là đường cao

c: BD=CD=8/2=4(cm)

nên AD=3(cm)

2:

a: Xét ΔBAE và ΔBDE có

BA=BD

góc ABE=góc DBE

BE chung

=>ΔBAE=ΔBDE

=>DA=AE

b: BA=BD

EA=ED

=>BE là trung trực của AD

c: Xét ΔEAI vuông tại A và ΔEDC vuông tại D có

EA=ED

góc AEI=góc DEC

=>ΔEAI=ΔEDC

a: Xét ΔABC có

CI,BI là đường phân giác

CI cắt BI tại I

=>I là tâm đường tròn nội tiếp

=>AI là phân giác của góc BAC

=>góc BAI=góc CAI=90/2=45 độ

b: Xét ΔBDI vuông tại D và ΔBFI vuông tại F có

BI chung

góc DBI=góc FBI

=>ΔBDI=ΔBFI

=>ID=IF

Xét ΔCEI vuông tại E và ΔCFI vuông tại F có

CI chung

góc ECI=góc FCI

=>ΔCEI=ΔCFI

=>IE=IF=ID

a: \(BC=\sqrt{10^2-6^2}=8\left(cm\right)\)

b: Xét ΔBAE vuông tại B và ΔKAE vuông tại K có

AE chung

\(\widehat{BAE}=\widehat{KAE}\)

Do đó: ΔBAE=ΔKAE

Suy ra: EA=EK

hay ΔEAK cân tại E

a: ΔABC cân tại A có AM là trung tuyến

nên AM là trung trực của BC và AM là phân giác của góc BAC

=>D nằm trên đường trung trực của BC

=>DB=DC

=>ΔDBC cân tại D

b: Xét ΔABC có

AD,BD là phân giác

=>D là tâm đường tròn nội tiếp

=>CD là phân giác của góc ACB

câu a thôi được không, không bít chứng minh thẳng hàng ;-;

Làm ròi :v

https://hoc24.vn/cau-hoi/.5759012133128

a) Xét tam giác OAH và tam giác OBH có

góc OAH = góc OBH = 90 độ

OH là cạnh chung

góc AOH = góc BOH ( OH là đường phân giác góc O)

=> tam giác OAH = tam giác OBH ( cạnh huyền - góc nhọn)

Đăng lên lớp 12 ý

kiểm tra ko hỏi bài

Ktr tự làm