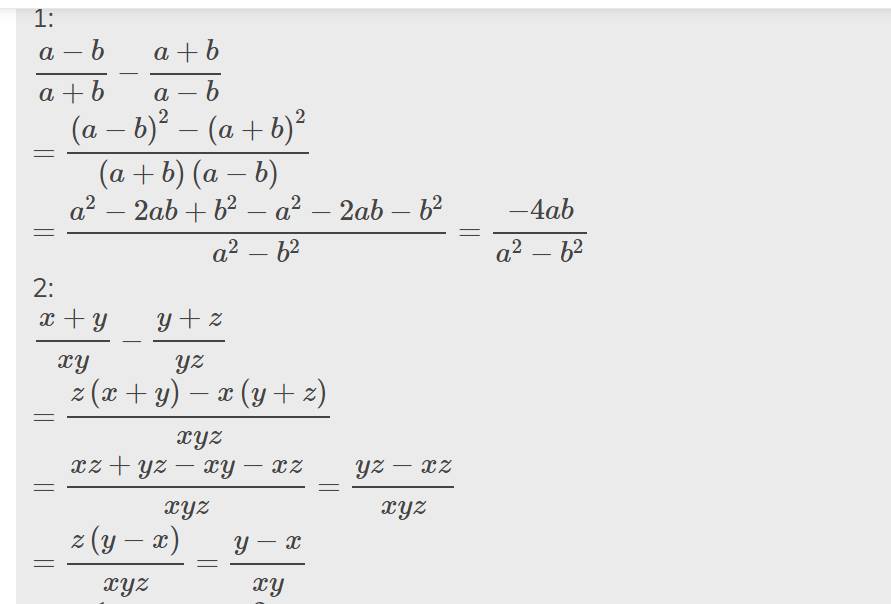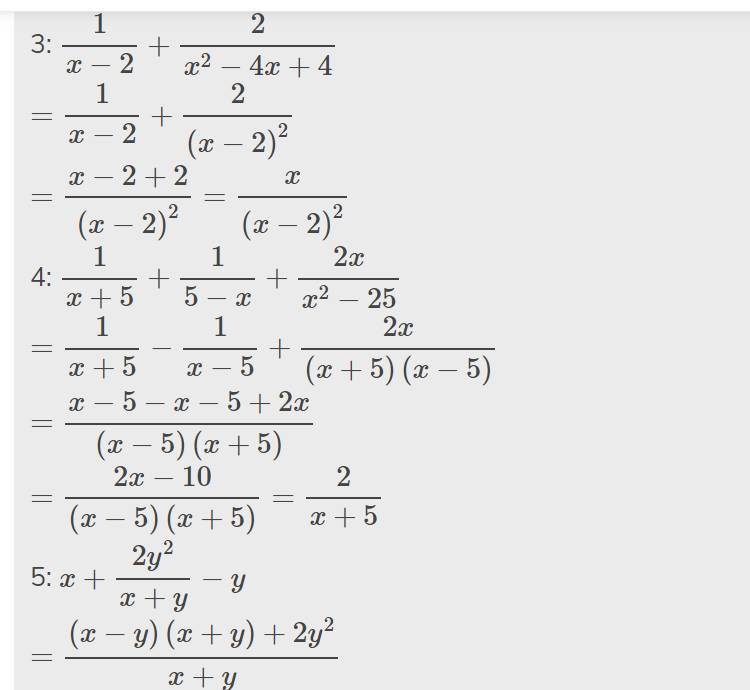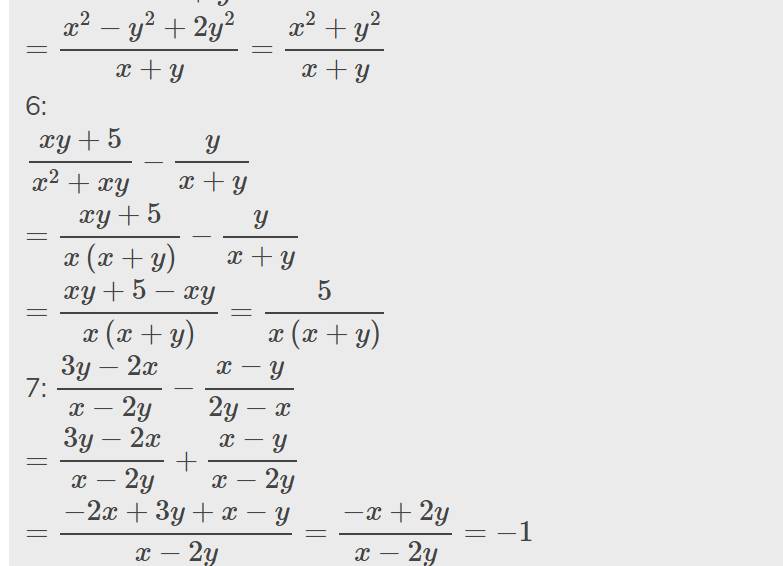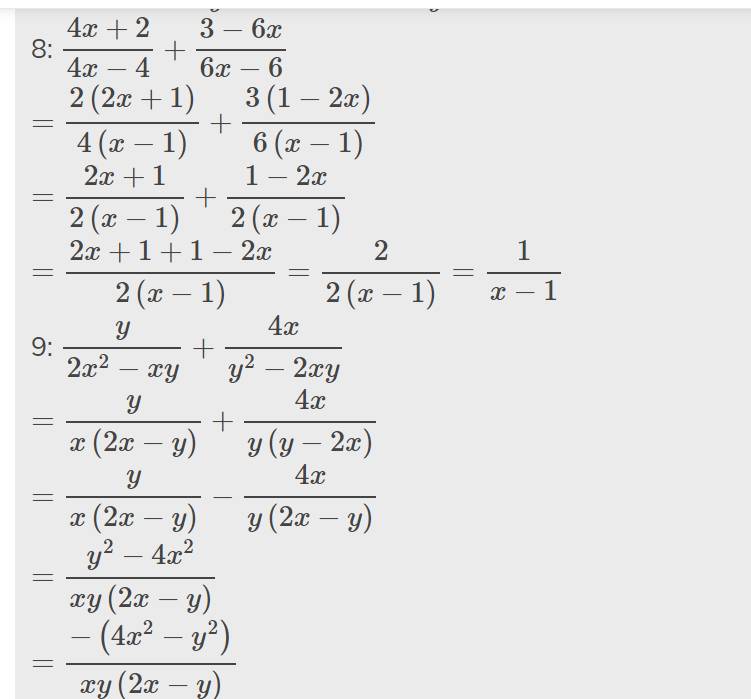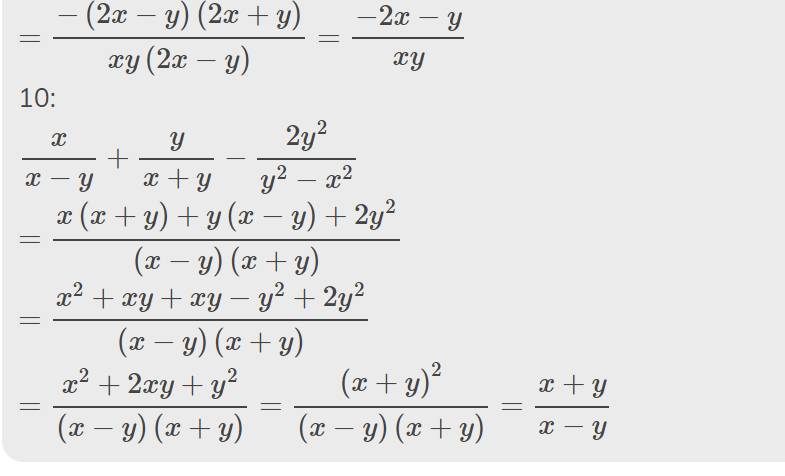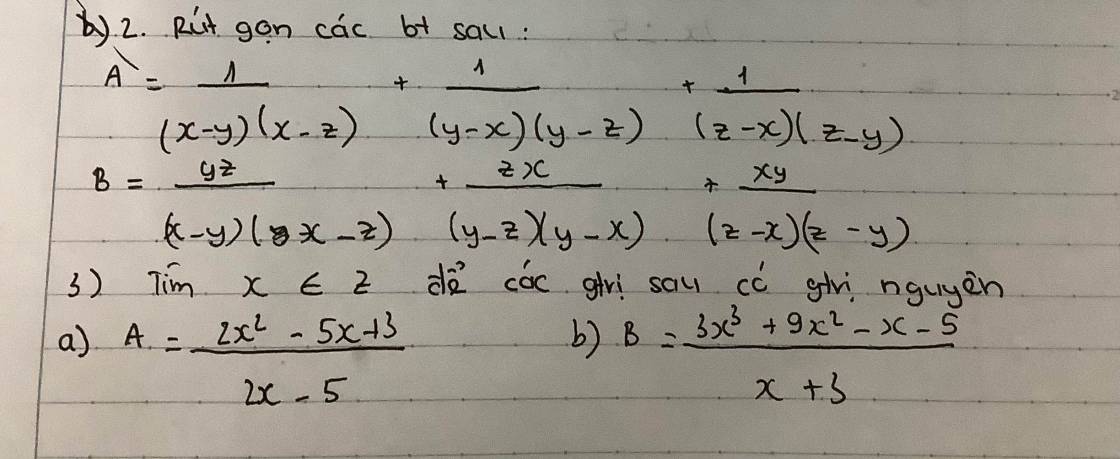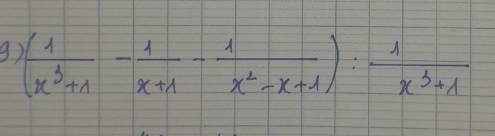
Bài 5: Phép cộng các phân thức đại số

5)

ĐK: \(x\ne\pm3\)

Biểu thức trở thành:

\(\dfrac{2x}{9-x^2}-\dfrac{\left(x+3\right)}{\left(3-x\right)\left(3+x\right)}-\dfrac{\left(3-x\right)}{\left(x+3\right)\left(3-x\right)}\\ =\dfrac{2x-x-3-3+x}{9-x^2}\\ =\dfrac{2x-6}{9-x^2}\\ =\dfrac{2\left(x-3\right)}{\left(3-x\right)\left(3+x\right)}\\ =-\dfrac{2\left(x-3\right)}{\left(x-3\right)\left(3+x\right)}\\ -\dfrac{2}{3+x}\)

6)

ĐK: \(x;y\ne0\)

\(\dfrac{8y}{3x^2}.\dfrac{9x^2}{4y^2}\\ =\dfrac{2.4y.3x^2.3}{3x^2.4y.y}\\ =\dfrac{6}{y}\)

7)

ĐK: \(x\ne-3\)

Biểu thức trở thành:

\(\dfrac{x\left(3+x\right)}{x^2+x+1}.\dfrac{3\left(x^3-1\right)}{x+3}\\ =\dfrac{x\left(3+x\right).3.\left(x-1\right)\left(x^2+x+1\right)}{\left(x^2+x+1\right)\left(3+x\right)}\\ =3x^2-x\)

8)

ĐK: \(x\ne\pm4\)

Biểu thức trở thành:

\(\dfrac{2\left(x+5\right)}{\left(x-4\right)\left(x^2+4x+16\right)}.-\dfrac{2\left(x-4\right)}{\left(x+5\right)\left(x+5\right)}\\ =-\dfrac{2\left(x+5\right).2.\left(x-4\right)}{\left(x-4\right)\left(x^2+4x+16\right)\left(x+5\right)\left(x+5\right)}\\ =-\dfrac{4}{\left(x+5\right)\left(x^2+4x+16\right)}\\ =-\dfrac{4}{x^3+4x^2+16x+5x^2+20x+80}\\ =-\dfrac{4}{x^3+9x^2+36x+80}\)

`HaNa♬D`

\(9,\left(\dfrac{1}{x^3+1}-\dfrac{1}{x+1}-\dfrac{1}{x^2-x+1}\right):\dfrac{1}{x^3+1}\left(x\ne1\right)\\ =\left(\dfrac{1}{\left(x+1\right)\left(x^2-x+1\right)}-\dfrac{1}{x+1}-\dfrac{1}{x^2-x+1}\right)\cdot\left(x^3+1\right)\\=\left(\dfrac{1}{\left(x+1\right)\left(x^2-x+1\right)}-\dfrac{x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}-\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}\right)\cdot\left(x^3+1\right)\\=\dfrac{1-x^2+x-1-x-1}{\left(x+1\right)\left(x^2-x+1\right)}\cdot\left(x^3+1\right)\\=\dfrac{\left(-x^2-1\right)\left(x^3+1\right)}{\left(x+1\right)\left(x^2-1+1\right)}\\ =-x^2-1\)

10) Thời gian để xe tải đi hết 300km:

\(\dfrac{300}{x}\left(h\right)\left(x\ne0\right)\)

Thời gian để xe khách đi hết 300km:

\(\dfrac{300}{y}\left(h\right)\left(y\ne0\right)\)

Xe khách đi ít hơn thời gian xe tải đi là:

\(\dfrac{300}{y}-\dfrac{300}{x}\)

\(=\dfrac{300x}{xy}-\dfrac{300y}{xy}\)

\(=\dfrac{300x-300y}{xy}\)

\(=\dfrac{300\left(x-y\right)}{xy}\)

\(1,\dfrac{x}{x+y}-\dfrac{y}{y-x}\left(xy\ne0\right)\\ =\dfrac{x}{x+y}+\dfrac{y}{x-y}\\ =\dfrac{x\left(x-y\right)}{x^2-y^2}+\dfrac{y\left(x+y\right)}{x^2-y^2}\\ =\dfrac{x^2-xy+xy+y^2}{x^2-y^2}\\ =\dfrac{x^2+y^2}{x^2-y^2}\\ 2,\dfrac{1}{x-1}-\dfrac{2}{x^2-1}\left(x\ge0;x\ne1\right)\\ =\dfrac{1}{x-1}-\dfrac{2}{\left(x-1\right)\left(x+1\right)}\\ =\dfrac{x+1-2}{\left(x-1\right)\left(x+1\right)}\\ =\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}\\ =\dfrac{1}{x+2}\)

\(3,\dfrac{x+2}{x^2+xy}-\dfrac{y-2}{xy+y^2}\left(x,y\ne0\right)\\ =\dfrac{x+2}{x\left(x+y\right)}-\dfrac{y-2}{y\left(x+y\right)}\\ =\dfrac{y\left(x+2\right)}{xy\left(x+y\right)}-\dfrac{x\left(y-2\right)}{xy\left(x+y\right)}\\ =\dfrac{xy+2y-xy+2x}{xy\left(x+y\right)}\\ =\dfrac{2y+2x}{xy\left(x+y\right)}\\=\dfrac{2\left(y+x\right)}{xy\left(x+y\right)}\\ =\dfrac{2}{xy}\)

\(4,\dfrac{1}{2x^2-3x}-\dfrac{1}{4x^2-9}\left(x\ne\pm\dfrac{3}{2}\right)\\ =\dfrac{1}{x\left(2x-3\right)}-\dfrac{1}{\left(2x-3\right)\left(2x+3\right)}\\ =\dfrac{2x+3}{x\left(2x-3\right)\left(2x+3\right)}-\dfrac{x}{x\left(2x-3\right)\left(2x+3\right)}\\ =\dfrac{2x+3-x}{x\left(2x-3\right)\left(2x+3\right)}\\ =\dfrac{x+3}{x\left(2x-3\right)\left(2x+3\right)}\)

1:

\(\dfrac{a-b}{a+b}-\dfrac{a+b}{a-b}\)

\(=\dfrac{\left(a-b\right)^2-\left(a+b\right)^2}{\left(a+b\right)\left(a-b\right)}\)

\(=\dfrac{a^2-2ab+b^2-a^2-2ab-b^2}{a^2-b^2}=\dfrac{-4ab}{a^2-b^2}\)

2: 

\(\dfrac{x+y}{xy}-\dfrac{y+z}{yz}\)

\(=\dfrac{z\left(x+y\right)-x\left(y+z\right)}{xyz}\)

\(=\dfrac{xz+yz-xy-xz}{xyz}=\dfrac{yz-xz}{xyz}\)

\(=\dfrac{z\left(y-x\right)}{xyz}=\dfrac{y-x}{xy}\)

3: \(\dfrac{1}{x-2}+\dfrac{2}{x^2-4x+4}\)

\(=\dfrac{1}{x-2}+\dfrac{2}{\left(x-2\right)^2}\)

\(=\dfrac{x-2+2}{\left(x-2\right)^2}=\dfrac{x}{\left(x-2\right)^2}\)

4: \(\dfrac{1}{x+5}+\dfrac{1}{5-x}+\dfrac{2x}{x^2-25}\)

\(=\dfrac{1}{x+5}-\dfrac{1}{x-5}+\dfrac{2x}{\left(x+5\right)\left(x-5\right)}\)

\(=\dfrac{x-5-x-5+2x}{\left(x-5\right)\left(x+5\right)}\)

\(=\dfrac{2x-10}{\left(x-5\right)\left(x+5\right)}=\dfrac{2}{x+5}\)

5: \(x+\dfrac{2y^2}{x+y}-y\)

\(=\dfrac{\left(x-y\right)\left(x+y\right)+2y^2}{x+y}\)

\(=\dfrac{x^2-y^2+2y^2}{x+y}=\dfrac{x^2+y^2}{x+y}\)

6:

\(\dfrac{xy+5}{x^2+xy}-\dfrac{y}{x+y}\)

\(=\dfrac{xy+5}{x\left(x+y\right)}-\dfrac{y}{x+y}\)

\(=\dfrac{xy+5-xy}{x\left(x+y\right)}=\dfrac{5}{x\left(x+y\right)}\)

7: \(\dfrac{3y-2x}{x-2y}-\dfrac{x-y}{2y-x}\)

\(=\dfrac{3y-2x}{x-2y}+\dfrac{x-y}{x-2y}\)

\(=\dfrac{-2x+3y+x-y}{x-2y}=\dfrac{-x+2y}{x-2y}=-1\)

8: \(\dfrac{4x+2}{4x-4}+\dfrac{3-6x}{6x-6}\)

\(=\dfrac{2\left(2x+1\right)}{4\left(x-1\right)}+\dfrac{3\left(1-2x\right)}{6\left(x-1\right)}\)

\(=\dfrac{2x+1}{2\left(x-1\right)}+\dfrac{1-2x}{2\left(x-1\right)}\)

\(=\dfrac{2x+1+1-2x}{2\left(x-1\right)}=\dfrac{2}{2\left(x-1\right)}=\dfrac{1}{x-1}\)

9: \(\dfrac{y}{2x^2-xy}+\dfrac{4x}{y^2-2xy}\)

\(=\dfrac{y}{x\left(2x-y\right)}+\dfrac{4x}{y\left(y-2x\right)}\)

\(=\dfrac{y}{x\left(2x-y\right)}-\dfrac{4x}{y\left(2x-y\right)}\)

\(=\dfrac{y^2-4x^2}{xy\left(2x-y\right)}\)

\(=\dfrac{-\left(4x^2-y^2\right)}{xy\left(2x-y\right)}\)

\(=\dfrac{-\left(2x-y\right)\left(2x+y\right)}{xy\left(2x-y\right)}=\dfrac{-2x-y}{xy}\)

10:

\(\dfrac{x}{x-y}+\dfrac{y}{x+y}-\dfrac{2y^2}{y^2-x^2}\)

\(=\dfrac{x\left(x+y\right)+y\left(x-y\right)+2y^2}{\left(x-y\right)\left(x+y\right)}\)

\(=\dfrac{x^2+xy+xy-y^2+2y^2}{\left(x-y\right)\left(x+y\right)}\)

\(=\dfrac{x^2+2xy+y^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{\left(x+y\right)^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{x+y}{x-y}\)

gấp

3:

a: Để A là số nguyên thì 2x^2-5x+3 chia hết cho 2x-5

=>x(2x-5)+3 chia hết cho 2x-5

=>2x-5 thuộc Ư(3)

=>2x-5 thuộc {1;-1;3;-3}

=>x thuộc {3;2;4;1}

b: B là số nguyên

=>3x^2+9x-x-3-2 chia hết cho x+3

=>x+3 thuộc {1;-1;2;-2}

=>x thuộc {-2;-4;-1;-5}

`#040911`

`a)`

`x^2 + y^2 + 2xy - 25`

`= (x^2 + 2xy + y^2) - 25`

`= [ (x)^2 + 2*x*y + (y)^2] - 5^2`

`= (x + y)^2 - 5^2`

`= (x + y - 5)(x + y + 5)`

`b)`

`x^2 + 2x - 15`

`= x^2 + 5x - 3x - 15`

`= (x^2 + 5x) - (3x + 15)`

`= x(x + 5) - 3(x + 5)`

`= (x - 3)(x + 5)`

`c)`

`x^2 - x - 2`

`= x^2 - 2x + x - 2`

`= (x^2 - 2x) + (x - 2)`

`= x(x - 2) + (x - 2)`

`= (x + 1)(x - 2)`

`d)`

`3x^2 - 11x + 6`

`= 3x^2 - 9x - 2x + 6`

`= (3x^2 - 9x) - (2x - 6)`

`= 3x(x - 3) - 2(x - 3)`

`= (3x - 2)(x - 3)`

`a, (x+y)^2-25 = (x+y+5)(x+y-5)`.

`b, x^2+2x-15 = (x+1)^2-16 = (x-3)(x+5)`.

`c, x^2-x-2=(x-2)(x+1)`

`d, 3x^2-11x+6 = (3x-2)(x-3)`.

\(a)x^2+y^2+2xy-25\\ =\left(x+y\right)^2-5^2\\ =\left(x+y+5\right)\left(x+y-5\right)\\ b)x^2+2x-15\\ =x^2+2x+1-16\\ =\left(x+1\right)^2-4^2\\ =\left(x+1+4\right)\left(x+1-4\right)\\ =\left(x+5\right)\left(x-3\right)\\ c)x^2-x-2\\ x^2+x-2x-2\\ =x\left(x+1\right)-2\left(x+1\right)\\ =\left(x+1\right)\left(x-2\right)\\ d)3x^2-11x+6\\ =3x^2-2x-9x+6\\ =x\left(3x-2\right)-3\left(3x-2\right)\\ =\left(x-3\right)\left(3x-2\right)\)

2:

a: =3x^2-3xy-(5x-5y)

=3x(x-y)-5(x-y)

=(x-y)(3x-5)

b: =6x(2x-y)-3y(2x-y)

=(2x-y)(6x-3y)

=3(2x-y)^2

c: =x(a-b)-y(a-b)

=(a-b)(x-y)

d: =x^2(a-b)-y^2(a-b)

=(a-b)(x^2-y^2)

=(x-y)(x+y)(a-b)

e: \(=6y\left(2x^2-3xy-5y^2\right)\)

=6y(2x^2-5xy+2xy-5y^2)

=6y[x(2x-5y)+y(2x-5y)]

=6y(2x-5y)(x+y)

f: =5x(x-y)-10(x-y)

=(x-y)(5x-10)

=5(x-2)(x-y)

g: =3x-4x+3y-4y

=-x+y

h: =7x(x-y)+(x-y)

=(x-y)(7x+1)

k: =(5x)^2-(3x+3y)^2

=(5x-3y-3x)(5x+3x+3y)

=(8x+3y)*(2x-3y)

\(d,x+\dfrac{1}{x+1}-1\)

\(=\dfrac{x\left(x+1\right)}{x+1}+\dfrac{1}{x+1}-\dfrac{x+1}{x+1}\)

\(=\dfrac{x^2+x+1-x-1}{x+1}\)

\(=\dfrac{x^2}{x+1}\)

#Ayumu

a: \(=15x^2+105x+4x^2+x-20x-5\)

=19x^2+86x-5

b: \(=\dfrac{6x+4x+8}{5x+4}=\dfrac{10x+8}{5x+4}=2\)

c: \(=\dfrac{x^2+7x-12x-14-x^2+10x-21}{\left(x-7\right)\left(x+7\right)}\)

\(=\dfrac{5x-35}{\left(x-7\right)\left(x+7\right)}=\dfrac{5}{x+7}\)

d: \(=\dfrac{x^3+4x^2-5x^2-20x+3x+12}{x+4}=x^2-5x+3\)

hê lô

cho bài khó dzậy