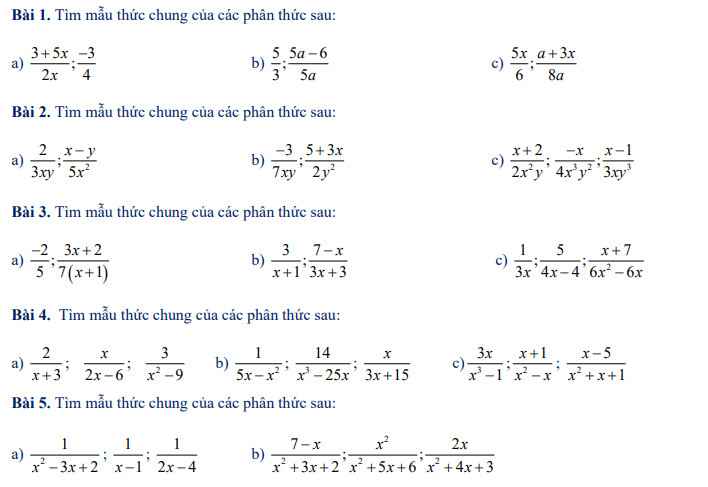Bài 4: Quy đồng mẫu thức nhiều phân thức

\(\dfrac{3}{x^2-5x}=\dfrac{3}{x\left(x-5\right)}=\dfrac{3.2}{2x\left(x-5\right)}=\dfrac{6}{2x\left(x-5\right)}\)

\(\dfrac{5}{2x-10}=\dfrac{5}{2\left(x-5\right)}=\dfrac{5.x}{2x\left(x-5\right)}=\dfrac{5x}{2x\left(x-5\right)}\)

\(\dfrac{3}{x^2-5x}và\dfrac{5}{2x-10}\)

\(x^2-5x=x\left(x-5\right)\)

\(2x-10=2\left(x-5\right)\)

MTC: \(2x\left(x-5\right)\)

\(\dfrac{3}{x^2-5x}=\dfrac{3.2}{\left(x^2-5x\right).2}=\dfrac{6}{2x\left(x-5\right)}\)

\(\dfrac{5}{2x-10}=\dfrac{5.x}{\left(2x-10\right).x}=\dfrac{5x}{2x\left(x-5\right)}\)

ta có 

`x^2-5x=x(x-5)`

`2x-10= 2x(x-5)`

`NTP: 2; 1`

Quy đồng :

`3/(x^2-5x)=(3.2)/((x^2-5x).2)=6/(2x(x-5))`

`5/(2x-10)=(5.1)/((2x-10).1)=5/(2x(x-5))`

\(\dfrac{x}{x^3-1}=\dfrac{x}{\left(x-1\right)\left(x^2+x+1\right)}\)

\(\dfrac{1+x}{1-x}=-\dfrac{x+1}{x-1}=\dfrac{-\left(x+1\right)\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)

Bài 5

a: MTC=2(x-1)(x-2)

b: MTC=(x+1)(x+2)(x+3)

Bài 4:

a: MTC=2(x-3)(x+3)

b: \(MTC=3x\left(x-5\right)\left(x+5\right)\)

c: \(MTC=\left(x-1\right)\cdot x\cdot\left(x^2+x+1\right)\)

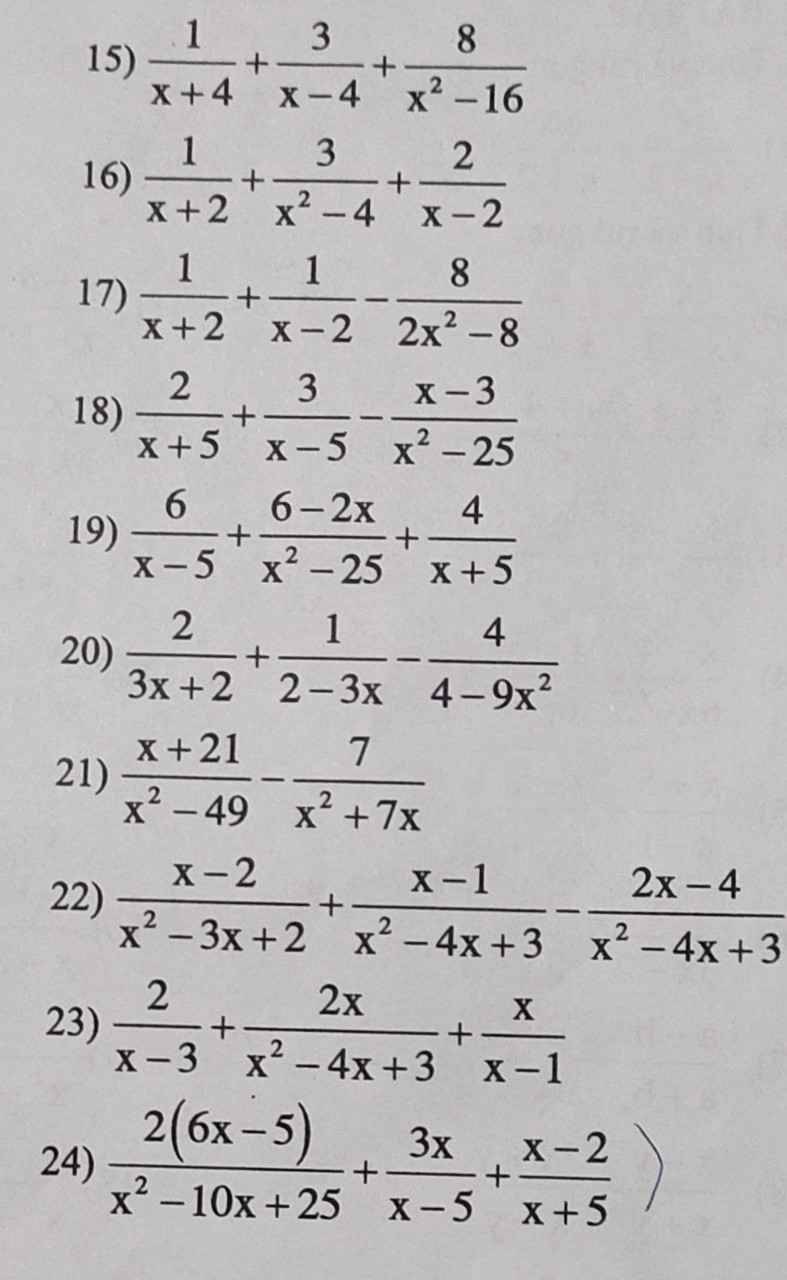
15: \(=\dfrac{x-4+3x+12+8}{\left(x-4\right)\left(x+4\right)}=\dfrac{4x+16}{\left(x-4\right)\left(x+4\right)}=\dfrac{4}{x-4}\)

16: \(=\dfrac{x-2+3+2x+4}{\left(x-2\right)\left(x+2\right)}=\dfrac{3x+5}{x^2-4}\)

17: \(=\dfrac{2x-4+2x+4-8}{2\left(x-2\right)\left(x+2\right)}=\dfrac{4x-8}{2\left(x-2\right)\left(x+2\right)}\)

\(=\dfrac{4\left(x-2\right)}{2\left(x-2\right)\left(x+2\right)}=\dfrac{2}{x+2}\)

19: \(=\dfrac{6x+30+6-2x+4x-20}{\left(x-5\right)\left(x+5\right)}=\dfrac{8x+16}{\left(x-5\right)\left(x+5\right)}\)

18: \(=\dfrac{2x-10+3x+15-x+3}{\left(x-5\right)\left(x+5\right)}=\dfrac{4x+8}{x^2-25}\)

20: \(=\dfrac{2\left(3x-2\right)-3x-2+4}{\left(3x-2\right)\left(3x+2\right)}\)

\(=\dfrac{6x-4-3x+2}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{3x-2}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{1}{3x+2}\)

\(\dfrac{x}{2x^2+7x-15}=\dfrac{x}{\left(x+5\right)\left(2x-3\right)}=\dfrac{x\left(x-2\right)}{\left(x+5\right)\left(2x-3\right)\left(x-2\right)}\)

\(\dfrac{x+2}{x^2+3x-10}=\dfrac{\left(x+2\right)\left(2x-3\right)}{\left(x+5\right)\left(2x-3\right)\left(x-2\right)}\)

\(\dfrac{1}{x+5}=\dfrac{\left(2x-3\right)\left(x-2\right)}{\left(x+5\right)\left(2x-3\right)\left(x-2\right)}\)

b: \(\dfrac{1}{-x^2+3x-2}=\dfrac{-1}{\left(x-1\right)\left(x-2\right)}=\dfrac{-x-6}{\left(x-1\right)\left(x-2\right)\left(x+6\right)}=\dfrac{\left(-x-6\right)\left(x-3\right)}{\left(x-1\right)\left(x-2\right)\left(x-3\right)\cdot\left(x+6\right)}\)

\(\dfrac{1}{x^2+5x-6}=\dfrac{1}{\left(x+6\right)\left(x-1\right)}=\dfrac{x-2}{\left(x+6\right)\left(x-1\right)\left(x-2\right)}\)

\(=\dfrac{\left(x-2\right)\left(x-3\right)}{\left(x+6\right)\left(x-1\right)\left(x-2\right)\left(x-3\right)}\)

\(\dfrac{1}{-x^2+4x-3}=\dfrac{-1}{\left(x-1\right)\left(x-3\right)}=\dfrac{-\left(x-2\right)\left(x+6\right)}{\left(x-1\right)\left(x-3\right)\left(x+6\right)\left(x-2\right)}\)

.

a: 1/4x=3y/12xy

3/6y=6x/12xy

b: xy/8=15xy/120

y/15=8y/120

c: x/2y=x^2/2xy

y/2x=y^2/2xy

b: xy/8=15xy/120

y/15=8y/120

c: x/2y=x^2/2xy

y/2x=y^2/2xy

\(=\dfrac{x+4}{x\left(x-4\right)}+\dfrac{4}{x\left(x+4\right)}+\dfrac{x+20}{\left(x-4\right)\left(x+4\right)}\)

\(=\dfrac{x^2+8x+16+4x-16+x^2+20x}{x\left(x+4\right)\left(x-4\right)}\)

\(=\dfrac{2x^2+32x}{x\left(x+4\right)\left(x-4\right)}=\dfrac{2x\left(x+16\right)}{x\left(x+4\right)\left(x-4\right)}=\dfrac{2\left(x+16\right)}{\left(x+4\right)\left(x-4\right)}\)

\(=\dfrac{x+4}{x\left(x-4\right)}+\dfrac{4}{x\left(x+4\right)}+\dfrac{x-20}{\left(x-4\right)\left(x+4\right)}\)

\(=\dfrac{\left(x+4\right)\left(x+4\right)}{x\left(x-4\right)\left(x+4\right)}+\dfrac{4\left(x-4\right)}{x\left(x-4\right)\left(x+4\right)}+\dfrac{x\left(x-20\right)}{x\left(x-4\right)\left(x+4\right)}\)
\(=\dfrac{x^2+8x+16+4x-16+x^2-20x}{x\left(x-4\right)\left(x+4\right)}\)
\(=\dfrac{2x^2-8x}{x\left(x-4\right)\left(x+4\right)}\)
\(=\dfrac{2x\left(x-4\right)}{x\left(x-4\right)\left(x+4\right)}\)
\(=\dfrac{2}{x+4}\)

Bạn ơi, đề bài nó bị lỗi rồi ấy, mình tải lại mấy lần rồi mà nó vẫn cứ vầy:

??

VÍ DỤ MẪU:

Ví dụ 1:

\(M=\dfrac{\left(2x^2-2\right)^2}{\left(x^2-2x+1\right)\left(x^2+2x+1\right)}\left(x\ne\pm1\right)\)

\(=\dfrac{\left(2x^2-2\right)^2}{\left(x-1\right)^2.\left(x+1\right)^2}=\dfrac{4\left(x^2-1\right)^2}{\left(x^2-1\right)^2}=4\)

Vậy .......

ví dụ 2:

\(N=\dfrac{\left(y+1\right)\left(y^2+5y+6\right)}{\left(y+3\right)\left(y^2+3y+2\right)}\left(y\ne-1;y\ne-2;y\ne-3\right)\)

\(=\dfrac{y^3+5y^2+6y+y^2+5y+6}{y^3+3y^2+2y+3y^2+9y+6}=\dfrac{y^3+6y^2+11y+6}{y^3+6y^2+11y+6}=1\)

Vậy ............

Ví dụ 3:

\(P=\dfrac{xy+2x+2y+4}{x+2}\left(x\ne-2\right)\)

\(=\dfrac{x\left(y+2\right)+2\left(y+2\right)}{x+2}=\dfrac{\left(x+2\right)\left(y+2\right)}{x+2}=y+2\)

Vậy ................

BÀI TẬP TỰ LUYỆN:

\(\dfrac{x^3+27y^3}{x^2-3xy+9y^2}=3.\dfrac{x^3+y^3}{x^2-xy+y^2}\)

\(\Leftrightarrow\dfrac{\left(x+3y\right)\left(x^2-3xy+9y^2\right)}{x^2-3xy+9y^2}=3.\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{x^2-xy+y^2}\)

\(\Leftrightarrow x+3y=3\left(x+y\right)\)

\(\Leftrightarrow x+3y=3x+3y\)

\(\Leftrightarrow2x=0\)

\(\Leftrightarrow x=0\)

Chọn A. x = 0